6. . Конденсатор в цепи синусоидального тока

Если приложенное к конденсатору напряжение не меняется во времени, то заряд q = Cu на одной его обкладке и заряд –q = -Cu на другой неизменны и ток через конденсатор не проходит ( ). Если же напряжение на конденсаторе меняется во времени, например, по синусоидальному закону:

U_c = U_msin t, (2.9)

то по синусоидальному закону будет меняться и заряд q конденсатора:

q = Cu = CU_msin t и конденсатор будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него зарядного тока:

. (2.10)

Положительное направление тока через конденсатор ёмкостью C на рис.2.6а совпадает с положительным направлением напряжения на нем. Из рис. (2.6 в) видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90⁰. Амплитуда тока I_m равна амплитуде напряжения U_m, деленной на емкостное сопротивление:

.

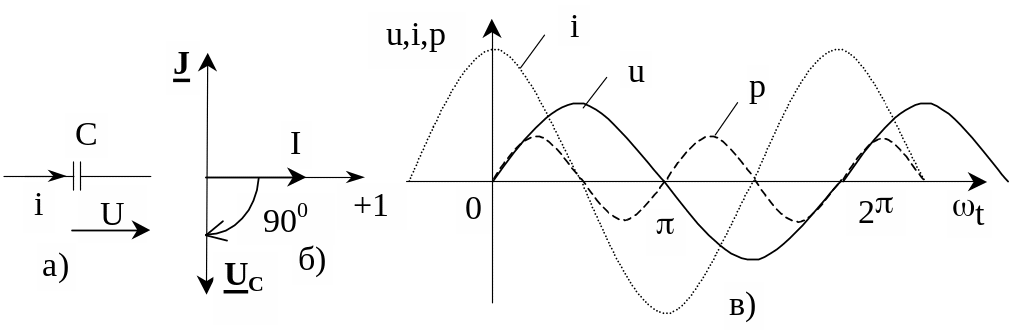
Рис. 2.6. Векторная и волновая диаграмма цепи с ёмкостью

Действительно, .

Емкостное сопротивление обратно пропорционально частоте. Единица емкостного сопротивления – Ом. Мгновенная мощность:

.

Графики мгновенных значений u, i, p изображены на рис. 2.6,в.

За первую четверть периода конденсатор потребляет от источника питания энергию, которая идет на создание электрического поля в нем. Во вторую четверть периода напряжение на конденсаторе уменьшается от максимума до нуля и запасенная в электрическом поле энергия отдается источнику (мгновенная мощность отрицательна). За третью четверть периода энергия снова запасается, за четвертую отдается и т.д. Комплекс действующего значения напряжения и тока

, при .

.

Векторная диаграмма цепи с ёмкостью показана на рис. 2.6,б.

Из последнего уравнения определяем комплекс действующего значения напряжения на ёмкости.

. (2.11)

2.7. Закон ома для цепи синусоидального тока. Комплексное сопротивление

Широкое распространение на практике получил символический, или комплексный, метод расчета цепей синусоидального тока.

Сущность символического метода расчета состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся дифференциальными уравнениями, к алгебраическим уравнениям, составленным относительно комплексов тока и Э.Д.С.

Например, для схемы рис.2.7 уравнение для мгновенных значений

u_R + u_L + u_C = e.

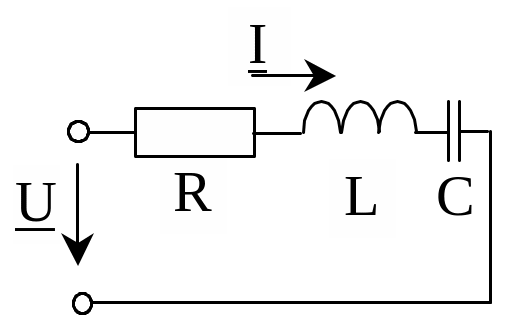
Рис. 2.7. Схема к расчёту цепи символическим методом

Для каждого члена уравнения было определено соответствующее ему выражение в комплексной форме. И так как цепь линейная, запишем его в комплексной форме.

Вынесем I за скобку:

(2.12)

Следовательно, для схемы рис. 2.7:

.

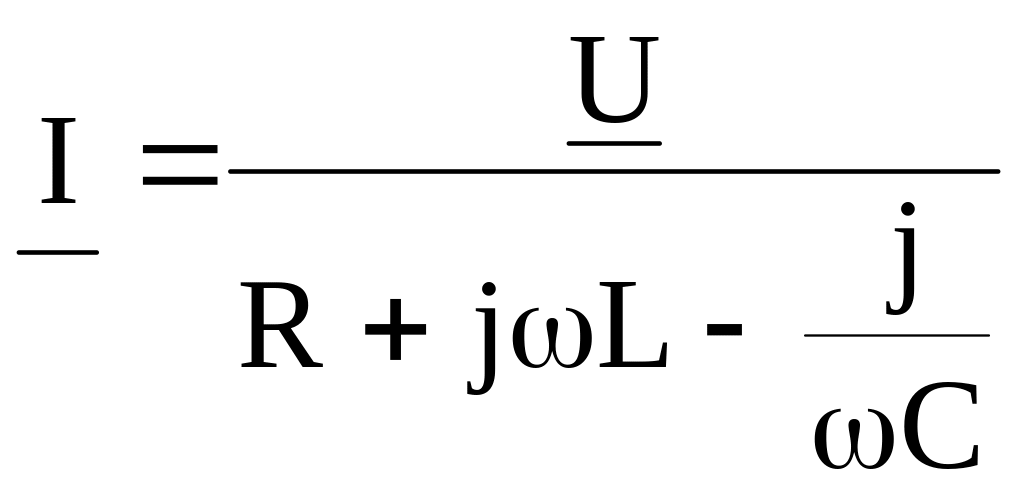Множитель R + jL – (j/C) в уравнении (2.12) представляет собой комплекс, имеет размерность сопротивления и обозначается через Z. Его называют полным комплексным сопротивлением:

.

Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать через Z. Уравнение (2.12) можно записать так: I Z = U. Откуда

. (2.13)

Уравнение (2.13) представляет собой закон Ома для цепи синусоидального тока.

В общем случае Z в комплексном виде имеет некоторую действительную часть R и некоторую мнимую часть jX

Z = R + jX,

где R – активное сопротивление; Х – реактивное сопротивление.

Для схемы рис.2.7 реактивное сопротивление:

.

Из уравнения (2.13)

, (2.14)

где - активная составляющая напряжения.

- реактивная составляющая напряжения.