55

Л3-4. Режим гармонических колебаний

Переменным током называют ток, изменяющийся во времени. Значение тока в любой данный момент времени называют мгновенным током i. Для одного из двух возможных направлений тока через поперечное сечение проводника мгновенный ток i считают положительным, а для противоположного направления отрицательным. Направление тока, для которого его мгновенные значения положительны, называют положительным направлением тока. Ток определен, если известна зависимость мгновенного тока от времени i = F(t) и указано его положительное направление.

Токи, мгновенные значения которых повторяются через равные промежутки времени в той же самой последовательности, называют периодическими.

Мгновенное значение синусоидального тока определяется выражением:

(2.1)

где I_m - максимальное значение или амплитуда тока. Аргумент синуса называется фазой. Угол  равен фазе в начальный момент времени (t=0) и поэтому называется начальной фазой. Период Т- это время, за которое совершается одно полное колебания. Единица измерения - секунда (с). Частота равна числу колебаний в одну секунду . Единица измерения частоты f - герц (Гц). Угловая частота . Единица угловой частоты - рад/с или с^-1.

Вводя в (2.1) обозначение  для угловой частоты, получаем:

i = I_msin (t+).

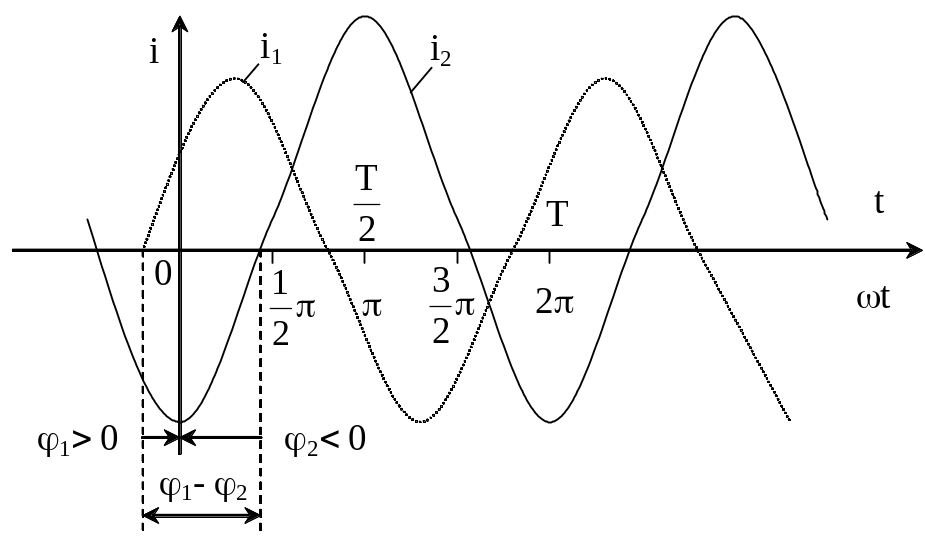
На рис. 2.1 дан график синусоидальных токов одинаковой частоты, но с различными амплитудами и начальными фазами:

i₁ ⁼ I_m1sin (t+₁) ; i₂ = I_m2sin (t+₂).

Р

ис. 2.1 график синусоидального тока

По оси абсцисс отложены время t и пропорциональная времени величина t.

Начальный фазный угол отсчитывается всегда от момента, соответствующего началу синусоиды (нулевое значение синусоидальной величины при переходе ее от отрицательных к положительным значениям), до момента начала отсчета времени t=0 (начало координат). При ₁>0 начало синусоиды (i₁) сдвинута влево, а при ₂<0 - (i₂) вправо от начала координат.

Если у нескольких синусоидальных функций, изменяющихся с одинаковой частотой, начала синусоид не совпадают, то говорят, что они сдвинуты друг относительно друга по фазе. Сдвиг фаз измеряется разностью фаз, которая, очевидно, равна разности начальных фаз. На рис. 2.1, например, ₁- ₂ > 0, т.е. ток i₁ опережает по фазе ток i₂ на угол ₁- _2, или, что то же самое, ток i₂ отстает по фазе от тока i₁ на угол ₁- ₂.

Если у синусоидальной функции одной частоты одинаковые начальные фазы, то говорят, что они совпадают по фазе, если разность их фаз равна ±, то говорят, что они противоположны по фазе, и, наконец, если разность их фаз равна ±/2, то говорят, что они находятся в квадратуре.

2.1. Действующие и средние значения тока, э.Д.С. И напряжения.

Для суждения о периодическом токе вводят понятие о среднем квадратичном значении тока за период, которое называется действующим током:

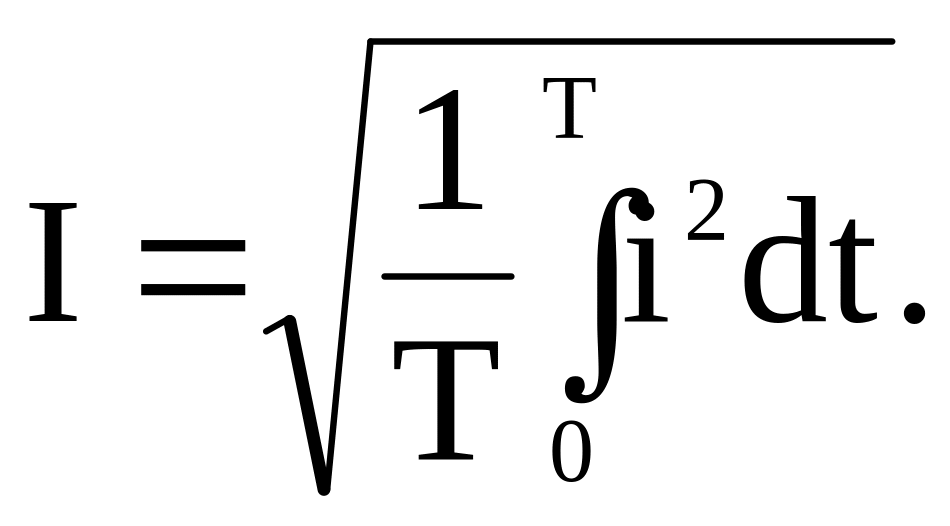(2.2)

Действующий ток численно равен такому постоянному току, который за один период выделяет в том же сопротивлении такое же количество тепла, как и ток переменный.

Установим связь между действующим током I и амплитудой I_m синусоидального тока:

Следовательно,

(2.3)

Среднеквадратичные значения любых других периодических величин за один период тоже называются действующими. Так, например, действующие Э.Д.С. и напряжение

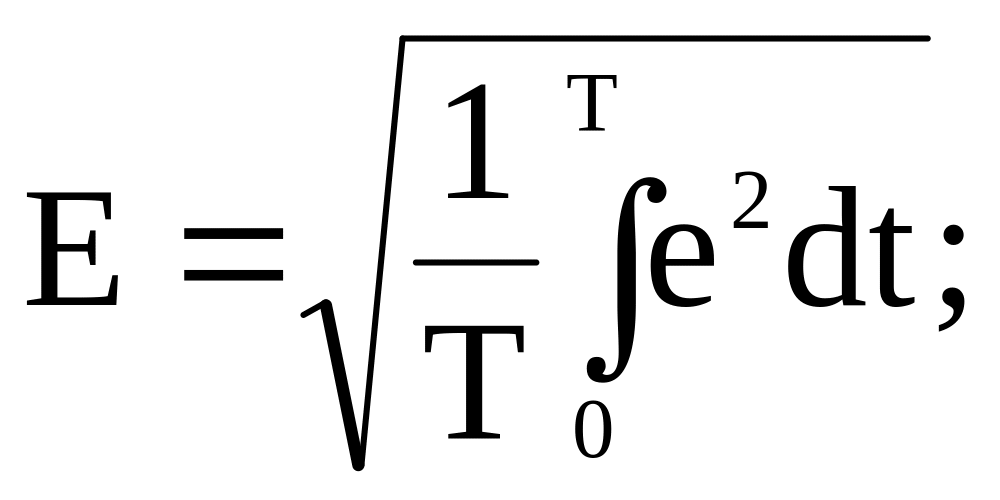
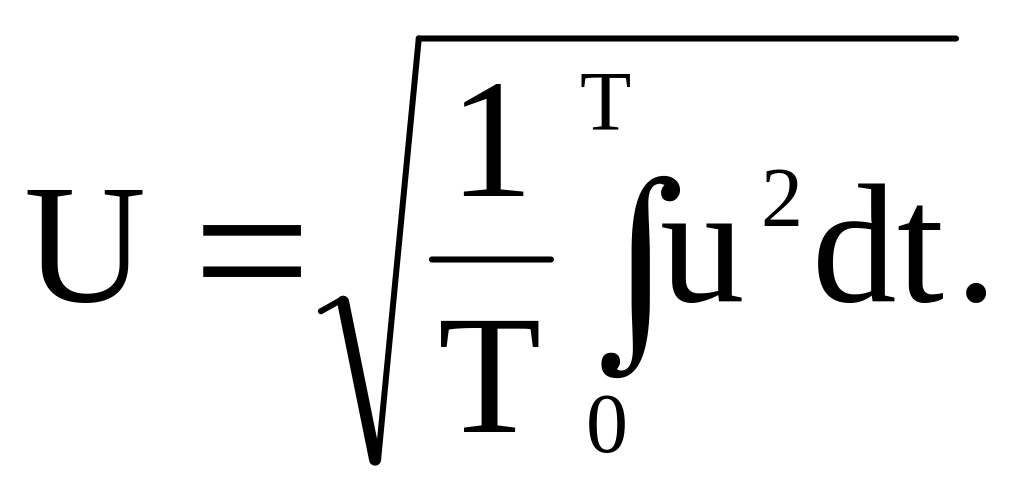
Когда речь идет о периодических напряжениях и токах, обычно подразумевают действующие напряжения и токи.

2.2. Изображение синусоидальных функций времени векторами и комплексными числами

Расчет цепей переменного тока облегчается, если изображать синусоидально изменяющиеся токи, напряжения и Э.Д.С. векторами или комплексными числами.

Пусть ток изменяется по синусоидальному закону

i=I_m(sint+).

Возьмем прямоугольную систему координат и расположим под углом  относительно горизонтальной оси ОХ вектор , длина которого равна I_m. Положительные углы  откладываются против, а отрицательные - по направлению часовой стрелки (рис2.2).

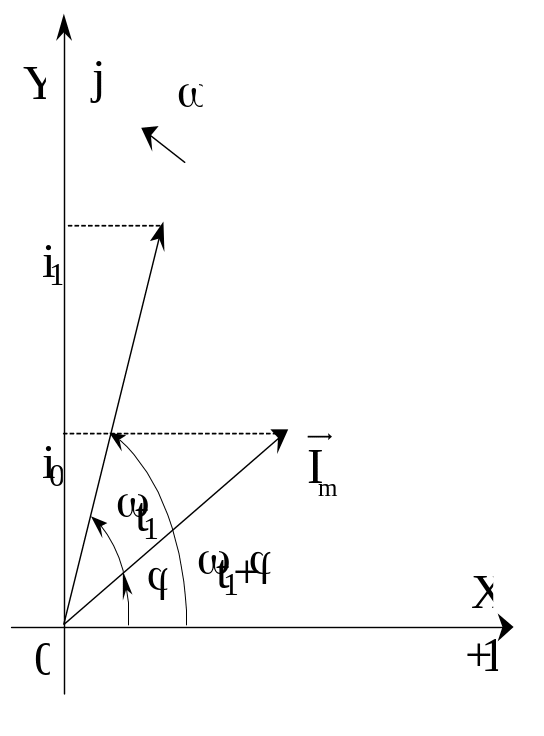
Рис.2.2. Векторная диаграмма тока.

Представим, что вектор с момента t = 0 начинает вращаться вокруг начала координат 0 против направления движения часовой стрелки с постоянной угловой скоростью, равной угловой частоте . В момент времени t₁ вектор составит с осью ОХ угол t₁+. Его проекция на ось ОУ равна в выбранном масштабе мгновенному значению тока

i₁=I_msin(t₁+).

Таким образом, между мгновенным значением i и вектором можно установить однозначную связь. На этом основании вектор называют вектором, изображающим синусоидальную функцию времени. Совокупность векторов, изображающих рассматриваемые синусоидальные функции времени, называется векторной диаграммой.

Если считать оси ОХ и ОУ осями вещественных (действительных) и мнимых величин на комплексной плоскости, то вектор соответствует комплексному числу, модуль которого равен I_m, а аргумент углу . Это комплексное число I_m, называется комплексной амплитудой тока. Оно обозначается большой буквой, подчеркнутой внизу.

Комплексную амплитуду тока можно записать в полярной, показательной, тригонометрической и алгебраической формах:

(2.4)

где .

Если правую и левую часть уравнения (2.4) разделить на , то получим комплекс действующего значения тока.

Аналогичное уравнение можно получить для синусоидально изменяющегося напряжения и Э.Д.С.:

Если вектор , начиная с момента времени t = 0, вращается против направления движения часовой стрелки с угловой скоростью , то ему соответствует комплексная функция времени, которая называется комплексной мгновенной величиной:

Значение ее мнимой части (без j) равно рассматриваемой синусоидально изменяющийся величине j.

Таким образом, величина j и ее изображение комплексная амплитуда однозначно связаны следующим равенством:

где символ Im обозначает, что от комплексной функции времени, записанной в квадратных скобках, берется только значение мнимой части.

Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называется методом комплексных величин, методом комплексных амплитуд или комплексным методом расчета.