3.10.3. Полосно-пропускающие фильтры (ппф)

ППФ –пропускают в нагрузку полосу частот от ₁ до ₂. они собираются по Т или П –схеме (рис.3.16).

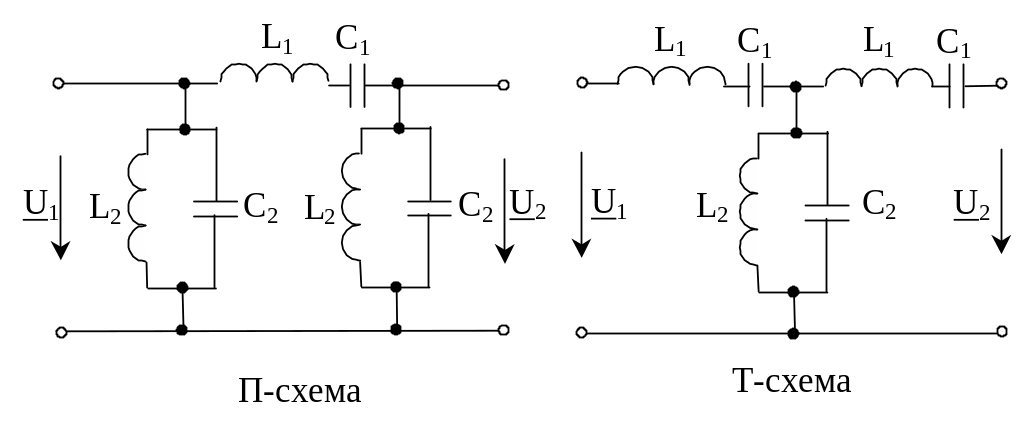
Рис.3.16. Схемы полосно-пропускающих фильтров

Параметры схем должны удовлетворять условию L₁C₁=L₂C₂. Тогда для частоты в продольной ветви наступает резонанс напряжений, а в поперечной – резонанс токов. Частотные характеристики коэффициентов затухания “a” и фазы “b” показаны на рисунке 3.17,а.

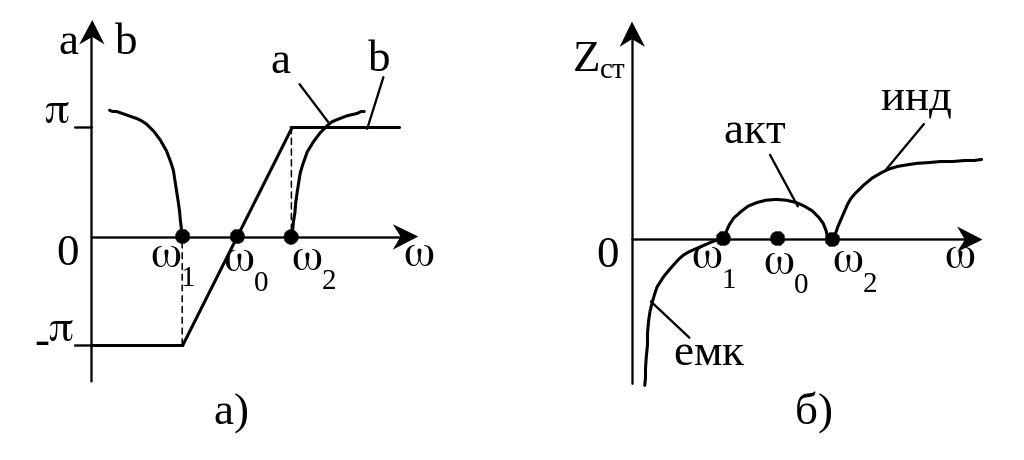
Рис. 3.17. График изменения коэффициента затухания, фазы и характеристического сопротивления ППФ, собранного по Т- схеме

Характеристические сопротивления ППФ также не остаются постоянными в полосе пропускания. Поэтому согласование фильтра с нагрузкой принципиально невозможно для всех частот полосы пропускания. Частотная характеристика Z_ст ППФ, собранного по Т- схеме, показана на рис. 3.17,б. Как видно из кривых рис. 3.17,б, вблизи резонансной частоты ₀, Z_ст изменяется медленно и остается почти постоянной. Поэтому если фильтр согласован с нагрузкой при частоте ₀, то это согласование распространяется на некоторые области частот, прилегающих справа и слева к частоте ₀.

3.10.4.Полосно-заграждающие фильтры (пзф)

В ПЗФ полоса прозрачности разрезана на две части полосой затухания. Например полоса прозрачности от 0₁ и от ₂. Они также собираются по Т и П- схеме (рис. 3.18).

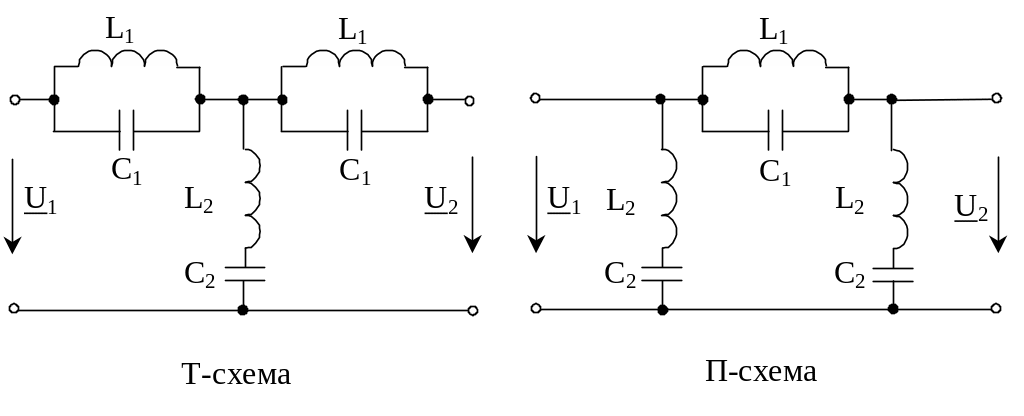
Рис.3.18.Схема полосно-заграждающих фильтров

Параметры схем должны удовлетворять условию: L₁C₁=L₂C₂. характер изменения “a”, ”b” и Z_ст для ПЗФ, собранного по Т- схеме показаны на рис. 3.19.

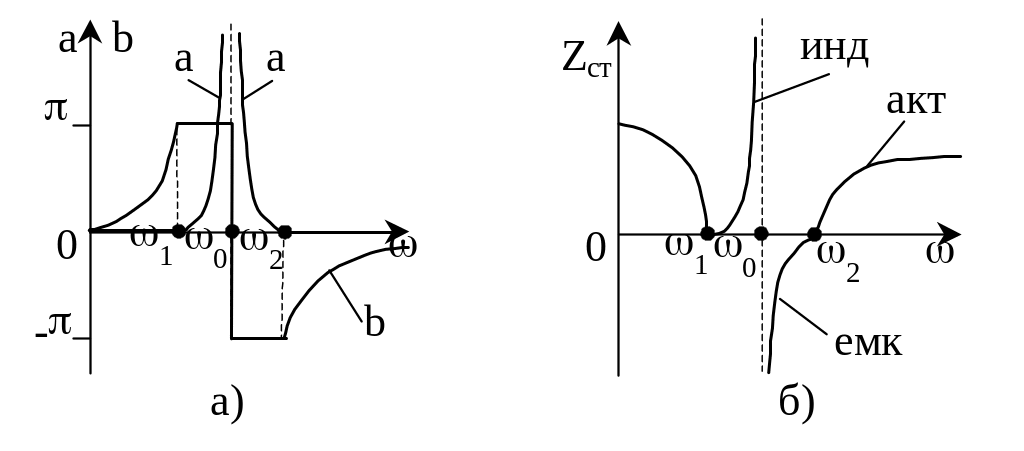
Рис.3.19. График изменения коэффициента затухания фазы и характеристического сопротивления для ПЗФ, собранного по Т- схеме

Применение Т или П- схем фильтра определяются условиями его работы и предъявляемыми к нему требованиями.

Например, пусть к линии, представляющей собой два канала –канал низкой и высокой частот, нужно подключить аппарат низкой частоты. Это можно сделать так, как показано на рис.3.20 при помощи низкочастотного фильтра, собранного по Т или П- схеме.

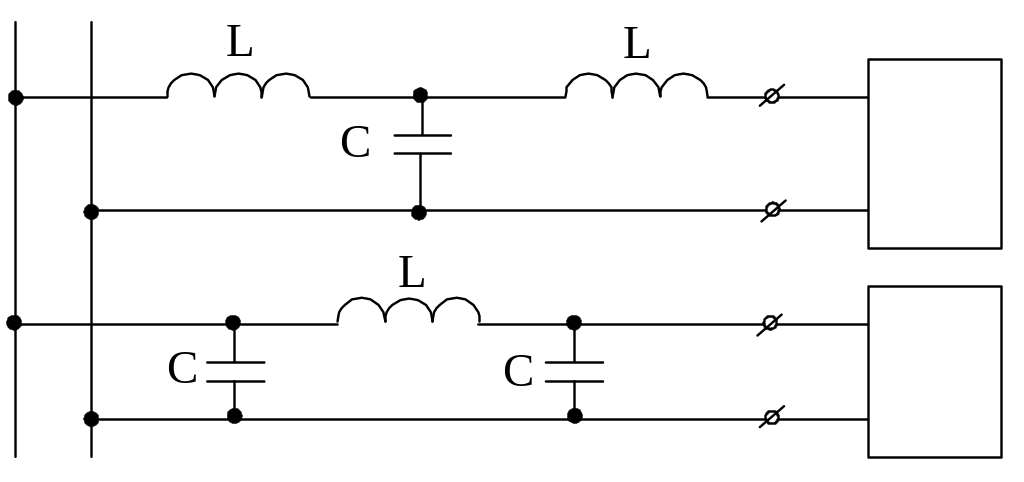
Рис.3.20. Схемы подключения к линии ФНЧ

Низкочастотный фильтр пропустит в аппарат токи низкой частоты и не пропустит токи высокой частоты. Однако в данном случае целесообразней выбрать «Т» схему, так как для «П» схемы токи высокой частоты замыкаются через конденсатор «С», что может ухудшить работу канала высокой частоты.

3.10.5. Rc- фильтры

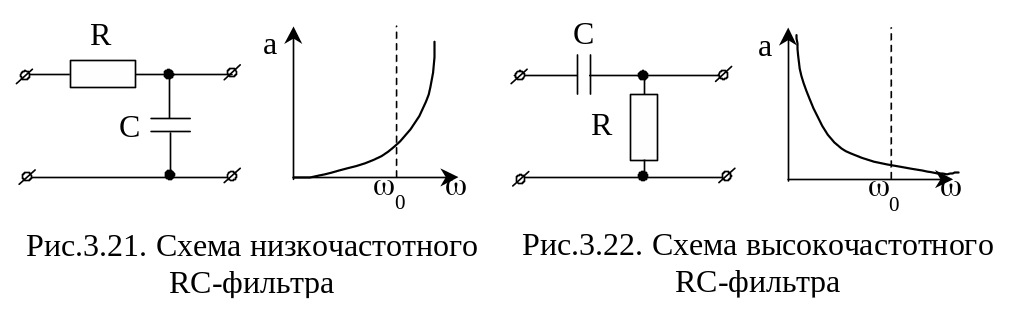
Если сопротивление нагрузки, на которую включен фильтр велико, то часто используют RC- фильтры: НЧ; ВЧ и полосно-пропускающие. Для всех RC-фильтров в рабочей зоне а0. Рабочая зона НЧФ – от 0 до ₀= , при которой а=0,343 Нп (рис.3.21). Для ВЧ-фильтра рабочая зона от ₀= , где а=0,343 Нп до  (рис.3.22).

В полосно-пропускающем фильтре минимальное затухание при ₀= , где а=0,343 Нп. (рис.3.23).

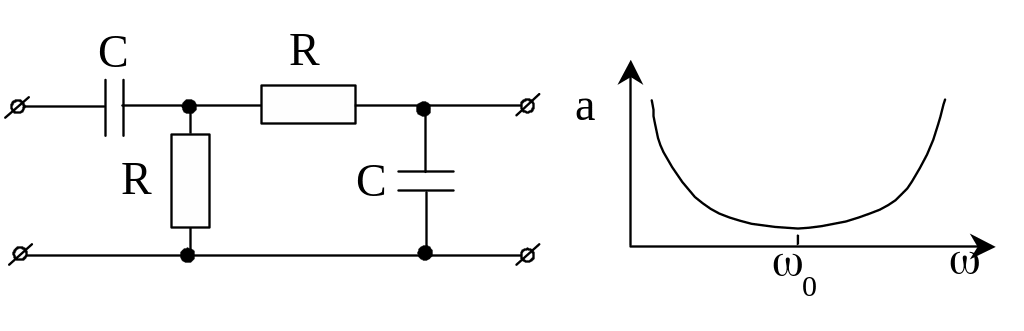
Рис.3.23. Схема полосно-пропускающего фильтра

3.11. Вопросы и задачи для самопроверки

1. Доказать, что в случае симметричного четырехполюсника, нагруженного согласованно, коэффициент передачи по напряжению равен:

.

2. Определить коэффициент передачи по напряжению при холостом ходе и коэффициент передачи по току при коротком замыкании для П-образного четырехполюсника, продольная ветвь которого состоит из L, а поперечная – из С (каждая).

3. Определить коэффициенты А-формы записи четырехполюсника, заменяющего воздушный трансформатор, если R₁=15 Ом, L₁=20 мГн, R₂=45 Ом, L₂=60 мГн, М=25 мГн, =1000 рад/с.

4. Рассчитать фильтр нижних частот с граничной частотой 1000 Гц и характеристическим сопротивлением 100 Ом при нулевой частоте.

5. Пояснить, исследуя формулы для симметричного фильтра без потерь, почему в полосе пропускания фильтра его характеристическое сопротивление активное, а в полосе затухания реактивное.

6. Как найти полосу пропускания фильтра по заданной частотной зависимости его характеристического сопротивления.

7. Пояснить физическую сущность коэффициента фазы фильтра.

8. Показать, что коэффициент передачи по напряжению в полосе пропускания для ФНЧ и ФВЧ, равен единице.