78

Л 5 Основы теории четырёхполюсников

Исследование режима работы электрических цепей часто сводится к установлению связи между токами и напряжениями двух ветвей электрической цепи. Так как каждая ветвь присоединяется к остальной части цепи в двух точках, то выделяется часть цепи с четырьмя зажимами, причем к одной паре зажимов (входной) обычно присоединяется источник, а к другой (выходной) нагрузка.

Часть электрической цепи произвольной конфигурации, имеющая две пары зажимов для присоединения к источнику и приемнику называется четырехполюсником. Четырехполюсники делятся на активные и пассивные. Четырехполюсники не содержащие в своих ветвях источников энергии, называются пассивными. К ним относятся линии передачи. Четырехполюсники, содержащие в своих ветвях источник энергии называются активным.

Четырехполюсники бывают симметричными и взаимными.

Симметричный четырехполюсник – тот, в котором перемена местами его входных и выходных зажимов не изменяет входных и выходных токов и напряжений.

Взаимные (обратимые) четырехполюсники это – четырехполюсники, для которых справедлива теорема взаимности.

Симметричные и пассивные линейные четырехполюсники всегда взаимны (обратимы). Несимметричные активные четырехполюсники невзаимны (необратимы). Четырехполюсники на электрических схемах обозначаются следующим образом:

Если четырехполюсники – активные, то внутри прямоугольника ставится буква А.

Зажимы mn обычно присоединяются к источнику (входные), pq – к нагрузке – выходные (рис. 3.1).

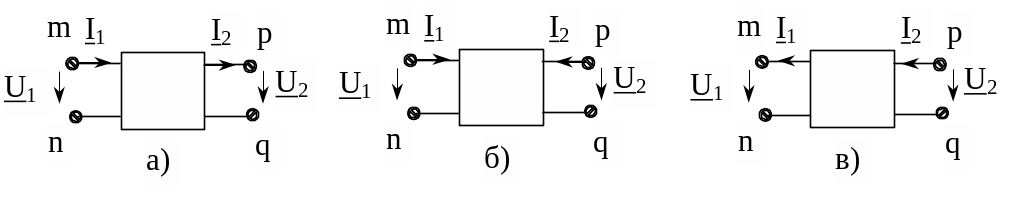
Рис.3.1 направление токов при различных формах записи уравнений четырёхполюсников

3.1. Шесть форм записи уравнений четырехполюсников

Число сочетаний из четырех по два (U₁,U₂,I₁,I₂) равно шести, поэтому возможны следующие шесть форм записи:

А – форма:

.

Y – форма:

.

Z – форма:

.

H – форма:

.

G – форма:

.

В – форма:

.

Исторически сложилось так, что для А-формы направление токов и напряжений соответствует рис.3.1,а - для Y и Z- формы; Н и G- формы – рис.3.1,б; для В- формы рис.3.1,в.

Для изучения теории и исследование режимов четырехполюсников, выведем уравнение А-формы записи четырехполюсников.

Напряжение на нагрузке U₂=I₂Z₂ (рис.3.2).

Рис.3.2. Схема четырёхполюсника с нагрузкой

На основании теоремы о компенсации Z₂ можно заменить на E₂=I₂Z₂ (Е₂ – направлена против тока (рис.3.3))

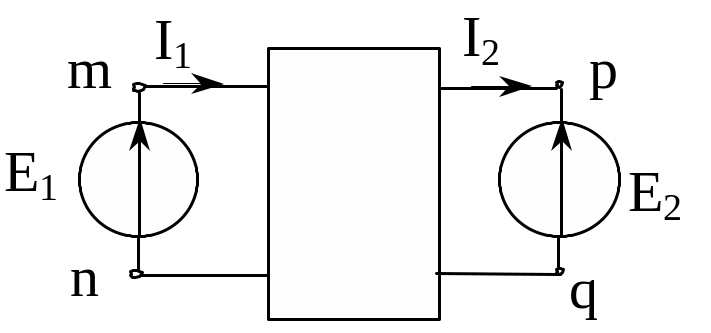
Рис.3.3. Замена сопротивления нагрузки на Э.Д.С.

По принципу наложения:

(3.1)

В этих уравнениях взято «-Е₂», так как оно направлено против токов, созданных Е₁. Напряжение U₁=E₁, U₂=E₂, тогда в (3.1):

(3.2)

Из уравнений (3.2):

(3.3)

или:

(3.4)

Коэффициенты четырехполюсника (взаимного) связаны соотношением:

.

Их значения зависят только от величин сопротивлений и конфигурации четырехполюсника.

Если в схеме рис.3.2 поменять местами источник и нагрузку, и изменить положительные направления токов I₁ и I_2­ (рис.3.4), то уравнение (3.4) примет

Рис.3.4. Схема четырёхполюсника при изменении мест включения источника и нагрузки

вид:

(3.5)

Из уравнения (3.5) с учетом, что AD – BC=1 получим:

(3.6)

Сравнивая (3.4) и (3.6) легко заметить, что при замене первичных зажимов вторичными коэффициенты А и D меняются местами.

Уравнение симметричного четырехполюсника должно в данном случае остаться неизменным. Поэтому у симметричного четырехполюсника A=D. Все четырехполюсники не удовлетворяющие этому условию являются несимметричными.