3. Расчет коэффициентов эластичности

Для множественного уравнения регрессии рассчитываются средние и частные коэффициенты эластичности.

Средние коэффициенты эластичности для множественной регрессии рассчитываются по формуле

(1.13)

где частные производные уравнения регрессии по соответствующему фактору; среднее значение соответствующего фактора x _i; среднее значение результативного признака.

Средний коэффициент эластичности показывает, насколько процентов в среднем изменится результат у с увеличением фактора х_i на 1 % от своего среднего уровня.

Для линейной множественной регрессии средние коэффициенты эластичности рассчитываются

(1.14)

где b _i - коэффициент чистой регрессии для соответствующего фактора x _i;

средние значения соответствующего фактора и результативного признака по совокупности показателей.

Средние коэффициенты эластичности можно сравнивать друг сдругом и соответственно использовать для ранжирования факторов по силе их влияния на результат. Чем больше величина , тем сильнее влияет фактор х_i на результат у.

Частные коэффициенты эластичности рассчитываются на основе частных уравнений регрессии, которые связывают результативный признак с соответствующими факторами х_i при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Для линейной множественной регрессии частные уравнения регрессии имеют следующий вид:

………………………………………………………………. (1.15)

При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т. е. имеем:

(1.16)

…………………………………

Эффекты влияния других факторов присоединены в них к свободному члену уравнения регрессии

С учетом частных уравнений регрессии для расчета частных коэффициентов эластичности применяется следующая формула:

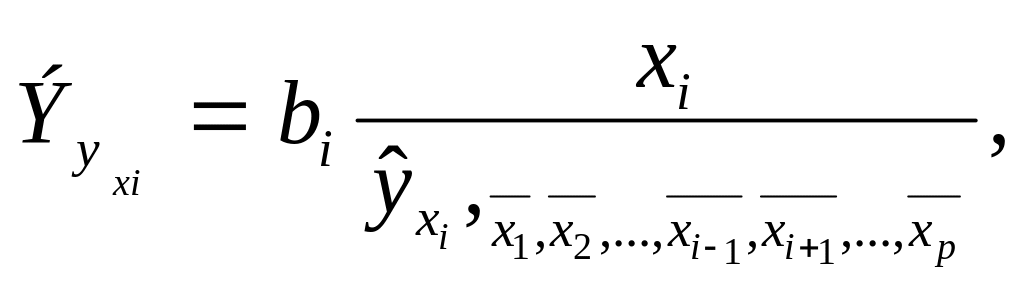(1.17)

где b _i - коэффициент регрессии для соответствующего фактора x _i в уравнении множественной регрессии;

- частная регрессия

Значения частных коэффициентов эластичности могут быть использованы при принятии решений относительно экономических явлений конкретных регионов, областей, предприятий и т. п.

4. Показатели корреляции и детерминации, их использование

Для множественной регрессии рассчитываются показатели множественной и частной корреляции.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым результативным признаком, т. е. оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

(1.18)

где общая дисперсия результативного признака;

остаточная дисперсия для уравнения с полным набором факторов.

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

При линейной зависимости признаков показатель множественной корреляции называется линейный коэффициент множественной корреляции или совокупный коэффициент корреляции, который может быть рассчитан по следующим формулам:

(1.19)

где стандартизованные коэффициенты регрессии;

парные коэффициенты корреляции результата с каждым фактором.

Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:

(1.20)

где определитель матрицы парных коэффициентов корреляции;

определитель матрицы межфакторной корреляции.

Для уравнения определитель матрицы коэффициентов парной корреляции примет вид:

(1.21)

определитель более низкого порядка: образуется, когда из матрицы коэффициентов парной корреляции вычеркиваются первая строка и первый столбец:

(1.22)

Для двухфакторного линейного уравнения регрессии совокупный коэффициент корреляции определяется по выражению вида:

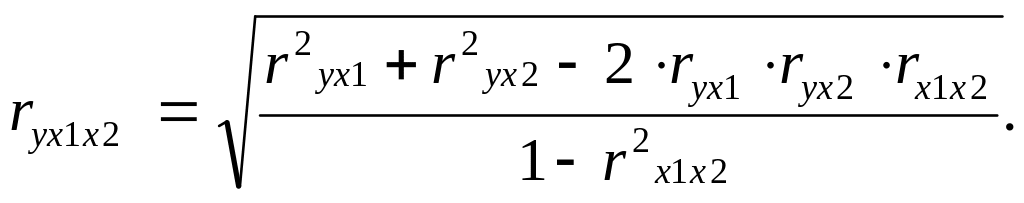(1.23)

Индекс множественной корреляции равен совокупному коэффициенту корреляции не только при линейной зависимости признаков, но и для криволинейной зависимости, нелинейной по переменным.

Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. В этом случае для оценки тесноты связи исследуемых признаков используется только индекс множественной корреляции .

Коэффициент (или индекс) множественной детерминации оценивает качество построенной модели в целом и рассчитывается как квадрат индекса множественной корреляции или квадрат совокупного коэффициента множественной корреляции:

или (1.24)

Если число параметров при х_i приближается к объему наблюдений n, то для оценки качества полученной многофакторной модели используется скорректированный индекс множественной детерминации, формула расчета которого имеет вид:

(1.25)

где k - число параметров при переменных х;

n - число наблюдений.

Чем больше величина k, тем сильнее различия и R².

Величина показателя множественной детерминации изменяется от 0 до 1. Низкое его значение означает, что в регрессионную модель не включены существенные факторы - с одной стороны, а с другой стороны – рассматриваемая форма связи выбрана неверно.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом у и соответствующим фактором x_i при устранении влияния других факторов, включенных в уравнение регрессии. Рассчитываются по формуле:

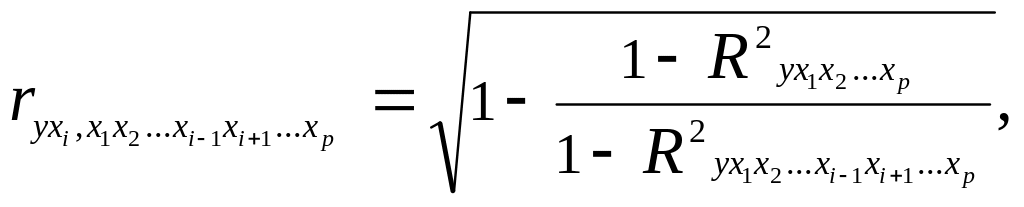(1.26)

где R² _yx1x2…xp- множественный коэффициент детерминации всего комплекса р факторов с результатом;

R² _{yx1x2…xi-1 xi+1…xp} - тот же показатель детерминации, но без введения в модель фактора x_i.

Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:

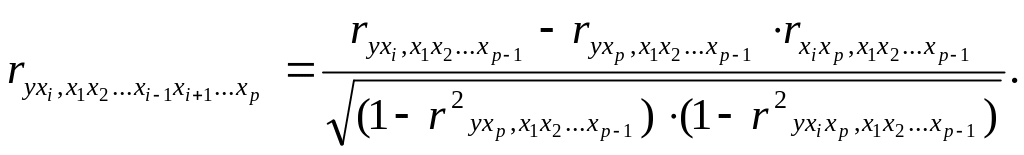(1.27)

При двух факторах и i =1 данная формула примет вид:

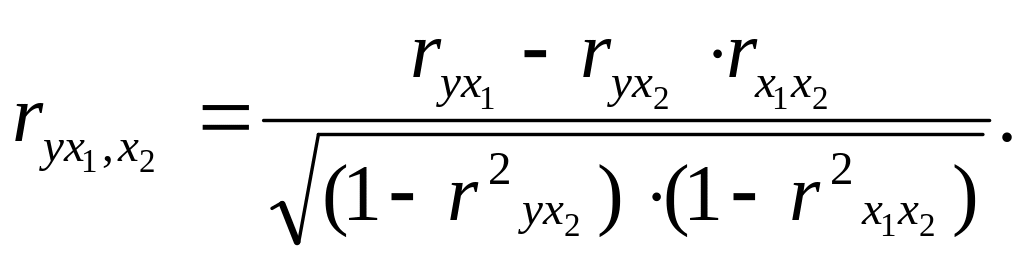(1.28)

Соответственно при i =2 частный коэффициент корреляции будет рассчитываться по формуле:

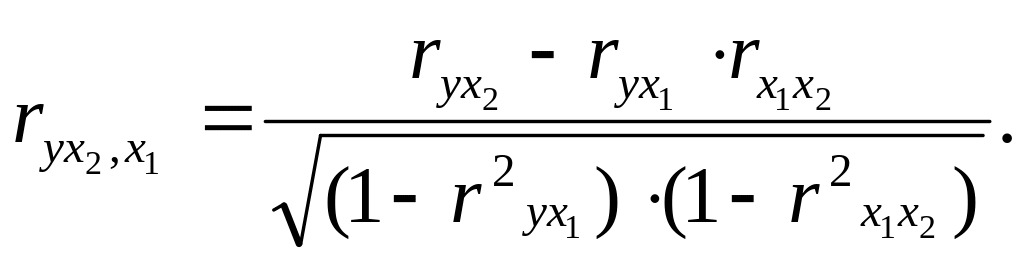(1.29)

Частные коэффициенты корреляции изменяются в пределах от –1 до +1. Величина множественного коэффициента корреляции всегда больше (или равна) максимального частного коэффициента корреляции.

При линейной зависимости исследуемых признаков частные коэффициенты корреляции могут быть использованы для ранжирования факторов, при нелинейной их взаимосвязи эту функцию выполняют частные индексы детерминации.

Кроме того, широко используются при решении проблемы отбора факторов.