3. Временные ряды в эконометрических исследованиях

Модели, построенные по данным, характеризующим объект за ряд последовательных моментов (периодов), называются моделями временных рядов.

Временной ряд – это совокупность значений какого либо показателя за несколько последовательных моментов или периодов.

Каждый уровень временного ряда формируется под воздействием трех компонент:

• трендовой компоненты, характеризующей основную тенденцию уровней ряда (Т);

• циклической компоненты, характеризующей циклические или периодические колебания изучаемого явления. Различают коньюктурную компоненту (К), связанную с большими экономическими циклами и сезонную компоненту (S), связанную с внутригодовыми колебаниями ряда;

• случайной компоненты, которая является результатом воздействия множества случайных факторов (Е).

Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение – мультипликативные модели временного ряда.

Аддитивная модель имеет вид:

; (3.1)

мультипликативная модель: . (3.2)

Аддитивную модель применяют, когда амплитуда сезонных колебаний со временем не меняется. Если амплитуда сезонных колебаний со временем возрастает или уменьшается, то применяют мультипликативную модель.

3. Выявление структуры временного ряда

Для выявления структуры ряда, т. е. состава компонент рассчитывают автокорреляцию уровней ряда.

Автокорреляция уровней ряда – это корреляционная зависимость между последовательными уровнями ряда.

Автокорреляция может быть измерена линейным коэффициентом корреляции ( r_i ) между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Сдвиг во времени (лаг) определяет порядок коэффициента автокорреляции.

Различают коэффициент автокорреляции первого, второго, третьего и т. д. порядков. Коэффициент автокорреляции уровней временного ряда первого порядка рассчитывают при лаге 1:

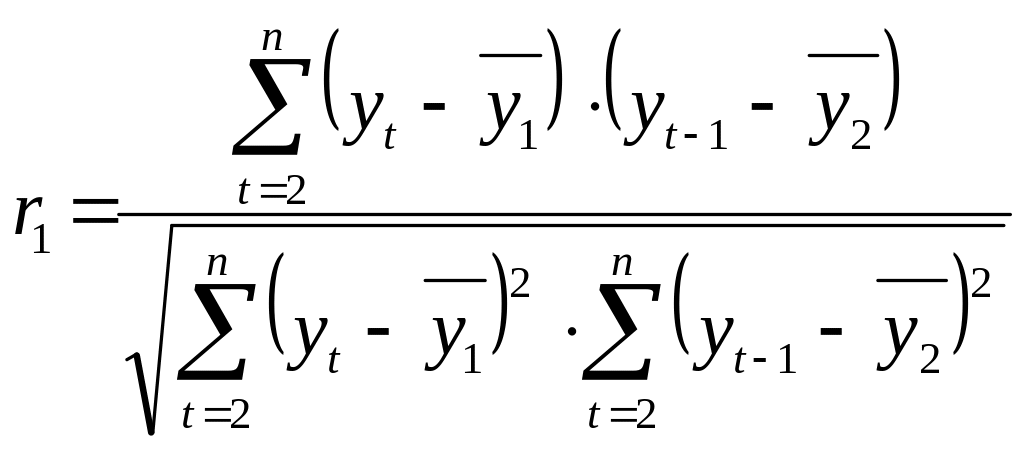, (3.3)

где - средний уровень исходного ряда, рассчитанный от t=2 до n; - средний уровень ряда, сдвинутого на один шаг, рассчитанный от t=2 до n.

Коэффициент автокорреляции уровней временного ряда второго порядка рассчитывают при лаге 2:

, (3.4)

где - средний уровень исходного ряда, рассчитанный от t=3 до n;

- средний уровень ряда, сдвинутого на два шага, рассчитанный от t=3 до n.

Обычно рекомендуют максимальный порядок коэффициента автокорреляции, равный n/4.

Рассчитав несколько коэффициентов автокорреляции можно определить лаг, при котором автокорреляция наиболее высокая, выявив тем самым структуру временного ряда.

Если наиболее высоким оказалось значение коэффициента автокорреляции первого порядка, то исследуемый временной ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка , ряд содержит циклические колебания с периодичностью в моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений:

• либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;

• либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.

Рассмотрим пример: пусть имеются данные предприятия по объемам выпуска некоторого товара по кварталам за 3 года в тыс. шт. (табл.3.1).

Таблица 3.1. – Объем выпуска товара, тыс. шт.

t	Yt	Yt-1			( )* ( )	( )2	( )2	Yt-2			( )* ( )	( )2	( )2
1	410	-	-	-	-	-	-	-	-	-	-	-	-
2	400	410	-368,64	-295,91	109084,3	135895,4	87562,73	-	-	-	-	-	-
3	715	400	-53,64	-305,91	16409,01	2877,25	93580,93	410	-90,5	-243	21991,5	8190,25	59049
4	600	715	-168,64	9,09	-1532,94	28439,45	82,6281	400	-205,5	-253	51991,5	42230,25	64009
5	585	600	-183,64	-105,91	19449,31	33723,65	11216,93	715	-220,5	62	-13671	48620,25	3844
6	560	585	-208,64	-120,91	25226,66	43530,65	14619,23	600	-245,5	-53	13011,5	60270,25	2809
7	975	560	206,36	-145,91	-30110	42584,45	21289,73	585	169,5	-68	-11526	28730,25	4624
8	800	975	31,36	269,09	8438,662	983,4496	72409,43	560	-5,5	-93	511,5	30,25	8649
9	765	800	-3,64	94,09	-342,488	13,2496	8852,928	975	-40,5	322	-13041	1640,25	103684
10	720	765	-48,64	59,09	-2874,14	2365,85	3491,628	800	-85,5	147	-12568,5	7310,25	21609
11	1235	720	466,36	14,09	6571,012	217491,6	198,5281	765	429,5	112	48104	184470,3	12544
12	1100	1235	331,36	529,09	175319,3	109799,4	279936,2	720	294,5	67	19731,5	86730,25	4489
	8865	7765	-0,04*	-0,01*	325638,6	617704,5	593240,9	6530	0	0	104535	468222,5	285310

* сумма не равна нулю в виду наличия ошибок округления.

.

Коэффициент автокорреляции первого и второго порядков составят:

Аналогично рассчитываются коэффициенты автокорреляции третьего, четвертого и пятого порядков, составившие: r₃ = 0,432; r₃ = 0,992; r₃ = 0,373.

Анализ рассчитанных коэффициентов автокорреляции позволяет сказать, что в данном ряду динамики имеется тенденция и сезонные колебания с периодом, равным 4.