33. Системы с информационной и решающей обратной связью.

В зависимости от назначения ОС различают системы: с решающей ОС (РОС), информационной ОС (ИОС) и комбинированной ОС (КОС).

В системах с РОС приемник, приняв кодовую комбинацию и проанализировав ее на наличие ошибок, принимает окончательное решение о выдаче комбинации потребителю информации или о ее стирании и посылке по обратному каналу сигнала о повторной передаче этой кодовой комбинации. В случае принятия кодовой комбинации без ошибок приемник формирует и направляет в канал ОС сигнал подтверждения, получив который, передатчик передает следующую кодовую комбинацию. Таким образом, в системах с РОС активная роль принадлежит приемнику, а по обратному каналу передаются вырабатываемые им сигналы решения.

В системах с ИОС по обратному каналу передаются сведения о поступающих на приемник кодовых комбинациях (или элементах комбинации) до их окончательной обработки и принятия заключительных решений. В общем случае приемник вырабатывает специальные сигналы, имеющие меньший объем, чем полезная информация, но характеризующие качество ее приема, которые по каналу ОС направляются передатчику. Если количество информации, передаваемое по ОС равно количеству информации в сообщении, то такая система – с полной ИОС. В обратном случае – с укороченной ИОС. Полученная по каналу ОС информация (квитанция) анализируется передатчиком, по результатам анализа передатчик принимает решение о передаче следующей кодовой комбинации или о повторении предыдущей.

В системах с КОС решение о выдаче кодовой комбинации или о повторной передаче может приниматься и в приемнике, и в передатчике, а канал ОС используется для передачи как квитанций, так и решений.

Недостаток ИОС: сложность приемного устройства

Недостаток РОС: обратный канал перегружен (TCP)

34. Свёрточные коды

В отличие от блочных кодов, где информационные и проверочные биты различимы, сверточные коды – непрерывные. Их кодирование и декодирование осуществляется без деления информационной части на блоки.

В основу формирования сверточных кодов положен принцип формирования проверочных разрядов с помощью суммы по модулю 2 каждого информационного разряда с некоторым набором предыдущих разрядов. Текущая кодовая комбинация сверточного кода зависит от того, что было передано раньше.

a₁(t), a₂(t), …, a_n-1(t) = f(a₁(t-1), a₂(t-1), …, a_n-1(t-1); a₁(t-2), a₂(t-2), …, a_n-1(t-2))

Сверточный кодер

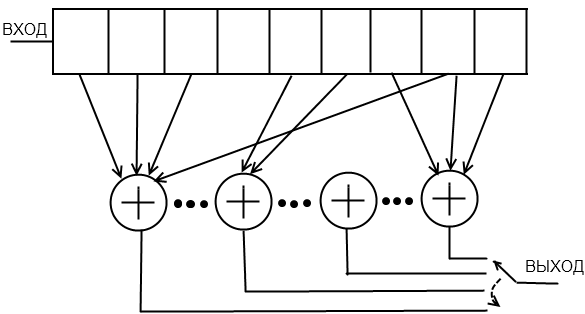
При поступлении каждого информационного разряда состояние регистра изменяется и ключ пробегает все сумматоры, выдавая на выход кодовую комбинацию.

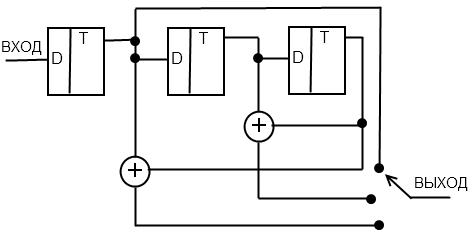
вход	состояние регистра	выход
001	000 100 010 001	000 101 010 011
010	000 000 100 010 001	000 000 101 010 011
011	000 100 110 011 001	000 101 111 001 011
100	000 000 000 100 010 001	000 000 000 101 010 011
101	000 100 010 101 010	000 101 010 110 010
110	000 000 100 110 011	000 000 101 111 001
111	010 100 110 111 011 001	000 101 111 100 001 011

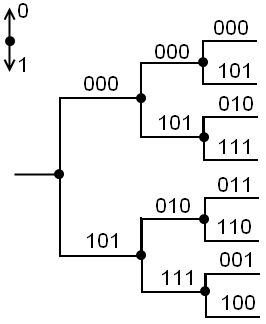
Удобным аппаратом декодирования является кодовое дерево. Точками кодового дерева обозначены узлы, соответствующие определенной последовательности на входе кодера.

Крайний слева узел соответствует моменту до начала поступления информации. Отрезки между соседними узлами – ребра. Совокупность последовательных ребер – ветвь. Для определения узла, соответствующего некоторой определенной информационной последовательности, двигаются с изначального узла кодового дерева, делая шаг вниз при поступлении «1» или шаг вверх – при «0». Вдоль ребер пишутся кодовые символы, генерируемые на выход кодера при переходе от данного узла к соседнему справа.

Число разрядов регистра = K

Число сумматоров = V

Длина последовательности = L

Длины выходной последовательности Y = (L+K)*V

Обычно L>>K, следовательно, производительность канала уменьшается в V раз.

Декодирование сверточных кодов.

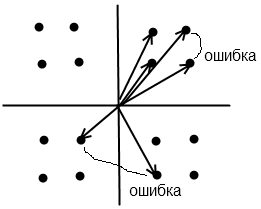
Одно из основных достоинств сверточного кода в том, что в кодово-модуляционном созвездии при квадратичной модуляции он создает определенные коррелированные связи между векторами на кодовое расстояние до уровня > d/2 (d=3), где d – количесвто разрядов.

Кодово-модуляционное созвездие:

Сначала m первых элементов подаются на 2 входных дешифратора, первый из которых выделяет комбинацию 101, второй – 000. В зависимости от того, какая комбинация попадает в m первых элементов, открывается путь к одной из пар дешифраторов. Подаются m вторых элементов.

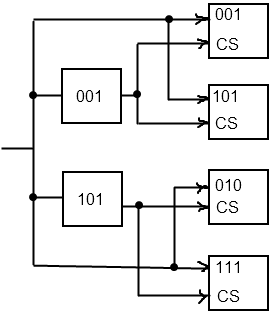
CS - кристалл

Кодовое дерево сверточного кодера/декодера

Например, при передаче последовательности 101,в дискретный канал поступает последовательность 101 010 110, которая при отсутствии ошибок декодируется в 101. При наличии ошибок в дискретном канале, отдельные группы, принятые кодовые комбинации (тройки) не будут совпадать с ребрами кодового дерева, при этом возможен механизм декодирования с исправлением ошибок (например, алгоритм Крафта – вероятностная процедура декодирования). При декодировании выбирается такая кодовая комбинация, которая отличается от принятой наименьшим числом разрядов.

Если принятая последовательность (тройка) не совпадает ни с одним узлом, выходящим из данного узла, то декодер следует сначала по ребру, у которого совпадающих символов больше.

Очевидно, что при числе ошибок в группе из m элементов, большим, чем m/2 декодер проследует к неправильному узлу. Однако, маловероятно, что сделав такую ошибку, декодер нашел в этом неправильном узле ребро, хорошо согласующееся с группой из m принятых элементов. При передаче информационной последовательности x = 1010 на выходе кодера получим:

Y = 11111 01010 11000 01001

При ошибке в канале e = 00010 01101 0000 0000

Тогда будет: 11101 00111 11000 01001

00111 ошибка 01010		00111 лучше 10101
01101 d=3		10010 d=2
11000 01101		11000 10010
10101 d=3 > d/2		11010 d=2

Декодер из начального узла 1 следует по правильному пути к узлу 2, а после него по неправильному пути в узел 3, т.к. 00111 отличается от 10101 в двух разрядах, а от 01010 в 3 разрядах.

У ребер, выходящих из узла 3 не совпадает столько же разрядов, сколько у правильного пути в узел 3’, что дает обоснование декодеру обнаружить ошибочный поворот и вернуться в узел 2 для исправления ошибки.

CDMA телефону применяют сверточное кодирование (10-20 мВт вместо 200 мВт).