28. Циклические коды. Синдром ошибки циклического кода. Операции над полиномами циклического кода и их особенности. Производящие полиномы циклических кодов.
Циклические коды были предложены в XVIII в. французским математиком Галуа.
Они позволяют обнаружить и исправить ошибки любой кратности. Используются в FrameRelay, PPP.
r |
Pr(x) |
Двоичное значение |
2 |
x2+x+1 |
111 |
3 |
x3+x+1 x3+ x2+1 |
1011 1101 |
4 |
x4+x+1 x4+ x3 +1 |
10011 11001 |
5 |
x5+ x4+ x3+ x2+1 x5+ x4+ x2+x+1 |
111101 110111 |
Умножение – остаток от деления на образующий полином полиномов, участвующих в умножении.
Умножение на х эквивалентно перемещению старшего разряда в младший, но оно не должно приводить к увеличению разрядности.
01010*х: (x3+x)*х = x4+ x2 (10100)
10100*х: (x4+ x2)*х = x5+ x3 (01001)
В передатчике каждая кодовая комбинация умножается на образующий полином и передается по каналу связи. В приемнике принятая комбинация делится на полином, известный на приеме и передаче. Если остаток от деления равен 0, то безошибочная передача, если остаток от деления не равен 0, то произошла ошибка и по обратному каналу может быть востребована повторная комбинация (если степень образующего полинома достаточно высока, производится исправление принятой комбинации по виду синдрома-остатка). Остаток от деления на приеме – синдром циклического кода.
29. Принцип формирования циклических кодов из информационных комбинаций передаваемых последовательностей. Обнаружение ошибок при циклическом кодировании.
Образование циклического кода на передачу:
1. Q(x)*xr, r - степень будущего образующего полинома.
2.
Pr(x) – образующий полином, имеет ту же степень, что и r.
R(x) – остаток от деления.
3.
4.
Вместо Q(x)*Pr(x) на передаче формируется слово (Q(x)* xr+R(x)), которое представляет из себя циклический код, т.к. он равен C(x)*Pr(x), а C(x) и Q(x) – кодовые комбинации 1го порядка.
Остаток от деления на приеме – синдром циклического кода.
n = k + r
2r = n + 1
Если исправляется одиночная ошибка, то количество остатков при ошибке в любом разряде должно быть равно разрядности слова (n), которое можно закодировать 2r синдромами. Если R(x)=0 – ошибок нет.
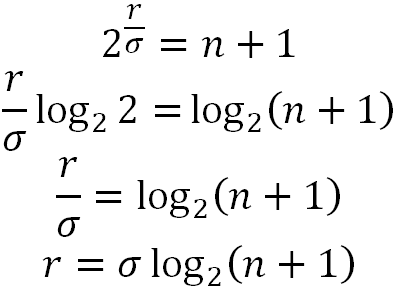
Хэммингово расстояние:
d = 2σ + 1 – для нечетных
d = 2σ + 2 – для четных
Декодирование циклических кодов.
Производится с использованием регистров обратной связи (ОС). Число триггеров равно степени образующих полиномов. Число сумматоров на единицу меньше веса образующего полинома. Сумматоры ставятся после каждого триггера, для которого существует ненулевой член полинома.
Pr(x) = x4+x+1
Pr(x) = 10011
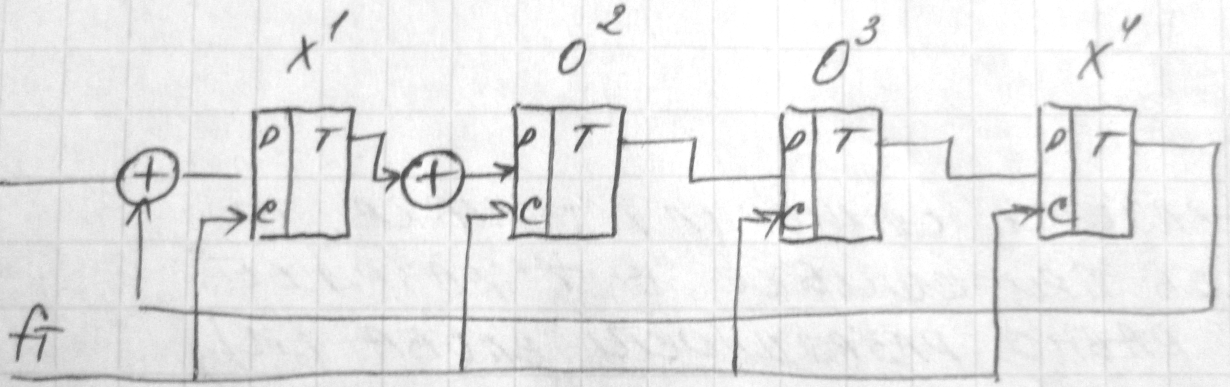
Q(x) = x4+x2+1
Q(x)* x4= x8+x6+ x4
F(x) = 101011010 (первые 5 - x4+x2+1, еще 4 – R(x))
Подаем комбинацию на схему декодера
Определение и исправление ошибки.
F(x) – передача
H(x) – прием
E(x) – ошибка
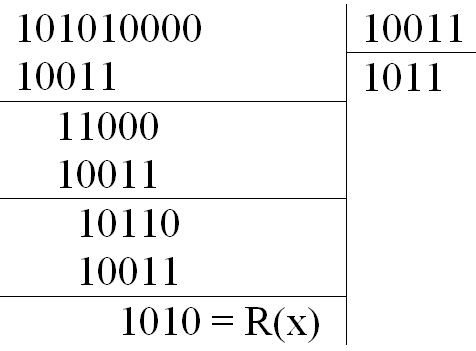
F(x) = H(x) + E(x) | :Pr(x)
При отсутствии ошибки H(x)/Pr(x) = F(x)/Pr(x)
Ошибка будет в том разряде, где будет 1 в полиноме ошибки при равных остатках.
F(x) = 101011010
H(x) = 111011010
E(x) = 010000000
1)
2)
Остатки совпали => ошибка во втором разряде.