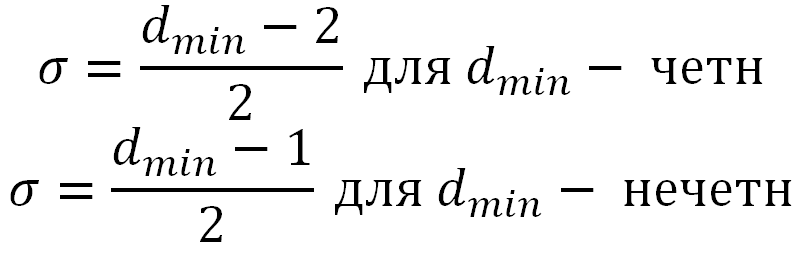21. Простые и корректирующие коды. Хэмминговое расстояние и вес кодовой комбинации. Контроль по четности.
По помехоустойчивости коды делят на простые (примитивные) и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются простыми, или кодами без избыточности. В простых равномерных кодах превращение одного символа комбинации в другой, например 1 в 0 или 0 в 1, приводит к появлению новой комбинации, т. е. к ошибке.
Корректирующие коды строятся так, что для передачи сообщения используются не все кодовые комбинации mn, а лишь некоторая часть их (так называемые разрешенные кодовые комбинации). Тем самым создается возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются введением в кодовые комбинации дополнительных (избыточных) символов.
Хэмминговым расстоянием между двумя кодовыми последовательностями b1 и b2 является число разрядов, в которых символы этих последовательностей не совпадают.
В канале произошла ошибка кратности q, если в кодовой комбинации q символов приянты ошибочно. Отсюда следует, что кратность ошибки – расстояние Хэмминга между переданной и принятой кодовыми комбинациями, или, иначе, вес вектора ошибки.
Код с контролем по четности – к каждой кодовой комбинации дополнительный элемент (1 или 0) для выравнивания четности по единицам, т.е. для сохранения триггером исходного состояния. Если на выходе триггера «1» - ошибка.
22. Вероятность ошибочного приема кодовых комбинаций при передаче информации простыми кодами.
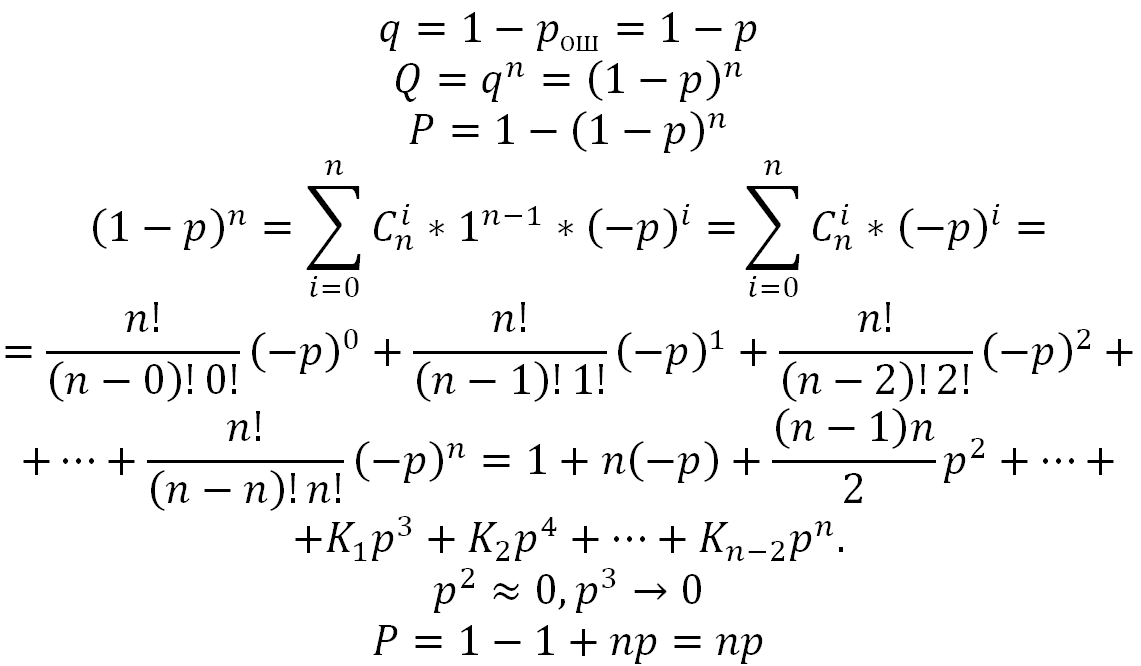
С увеличением кодовых комбинаций вероятность ошибки возрастает пропорционально.
23. Простейшие коды с обнаружением ошибок. Код с четным числом единиц. Коды с постоянными весами. Вероятности необнаруженной ошибки.
Код с контролем по четности.
000 |
0 |
001 |
1 |
010 |
1 |
011 |
0 |
100 |
1 |
101 |
0 |
110 |
0 |
111 |
1 |
Вероятность обнаруженной ошибки:
Следовательно,
вероятность обнаруженной ошибки
.
Вероятность необнаруженной ошибки
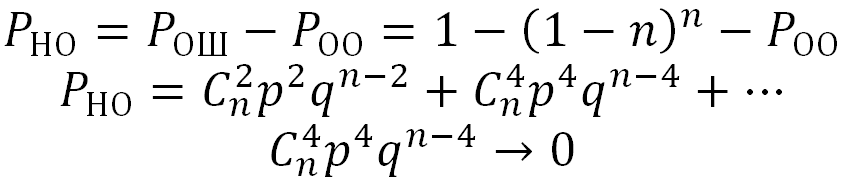
Коэффициент обнаружения ошибок
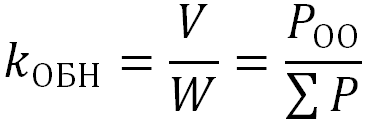
V – количество искаженных комбинаций, в которых ошибки обнаруживаются,
W – количество искаженных комбинаций, в которых ошибки обнаруживаются и не обнаруживаются.
Код с постоянным весом.
3:2
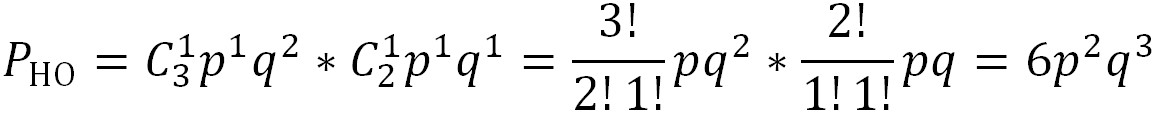
3:4
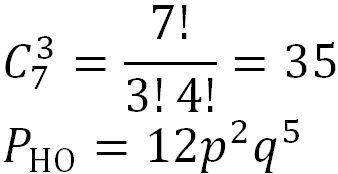
Позволяют обнаруживать одинарные, двойные и т.д. ошибки, кроме ошибок смещения.
Избыточность для кода 3:2 = 1,51, для 3:4 = 1,35.
Хэммингово расстояние для кода 3:2:
10110 11100 |
01010 |
d = 2, следовательно код 3:2 обнаруживает одинарные ошибки.
24. Корректирующие коды, проверочные и информационные элементы. Корректирующая способность кода. Соотношения между кратностью обнаруженных и корректируемых ошибок и Хэмминговым расстоянием кода.
Корректирующие коды (помехоустойчивые) разделяются на блочные и непрерывные (сверточные).
Блочные коды – коды, в которых каждому символу соответствует блок из N разрядов. Разделяются на равномерные и неравномерные (код Морзе).
Непрерывные коды представляют собой непрерывную последовательность символов, не разделенных на блоки.
Равномерные блочные коды: разделимые (информационные и проверочные элементы стоят на определенных позициях) и неразделимые (деление на информационные и проверочные отсутствует).
Разделимые: систематические, или линейные, (проверочные элементы формируются в результате линейных операций над информационными элементами) и несистематические, или нелинейные, (код с контролем по четности, итеративные коды)
Состояние канала во времени может изменяться. Адаптивно меняющий свою избыточность код – корректирующий код.
В N-элементном коде используются не все M=2n комбинаций, а Mинф =2k, остальные 2r – избыточные. n = k + r.
Количество обнаруживаемых ошибок – кратность обнаруживаемых ошибок, количество исправляемых ошибок – кратность исправляемых ошибок.
Кратность обнаруживаемых ошибок:
.
Кратность исправляемых ошибок:
