Лабораторная работа 3

Полнота метрических пространств

Примеры решения задач

Задача 1 Является ли последовательность фундаментальной в данном пространстве X? Найти , если он существует.

Пример 1 , ,

где K – канторово множество.

Решение. Так как канторово множество имеет лебегову меру нуль, то и - множество меры нуль. Значит, п.в.

Покажем, что сходится к 0 в . Для этого рассмотрим

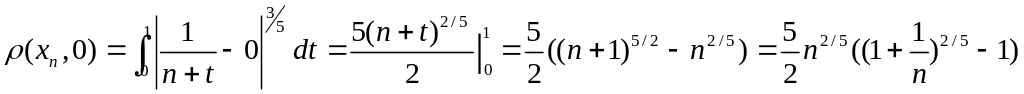
и воспользуемся разложением по формуле Тейлора:

при .

Получаем:

при .

Тот же результат мы получим, применив теорему Лебега о предельном переходе под знаком интеграла.

Итак, сходится к 0, а потому она фундаментальна.

Пример 2 , ,

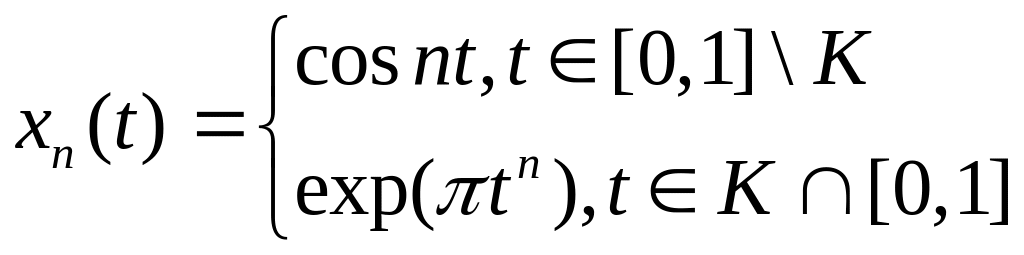Решение. Так как - множество меры нуль, то п.в. на [0;1]. Покажем, что эта последовательность не фундаментальна в нашем пространстве:

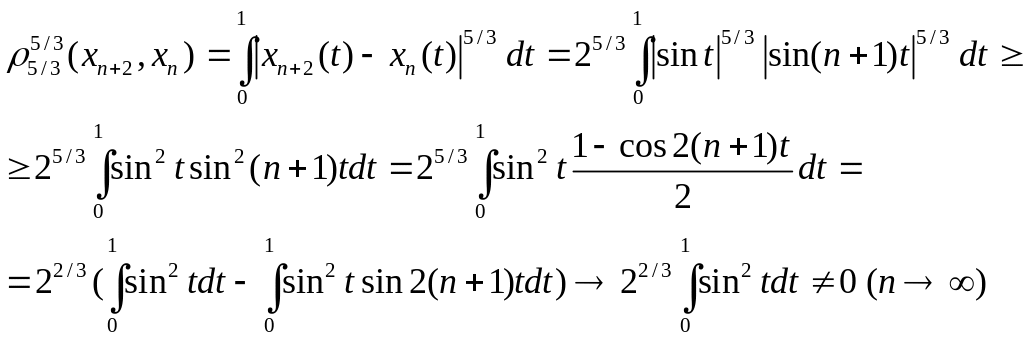
(мы воспользовались леммой Римана из теории рядов Фурье, согласно которой , но можно было бы вычислить интеграл и непосредственно).

Задача 2 Является ли метрическое пространство полным?

Пример 1 Х=B[0,1] ­ пространство вещественнозначных ограниченных функций на [0,1], наделенное метрикой

.

Решение. Покажем, что любая фундаментальная последовательность ( ) в B[0,1] является сходящейся. Ее фундаментальность значит, что : выполняется неравенство

(1)

Зафиксируем произвольное число . Тогда числовая последовательность ( ) в силу (1) является фундаментальной в R. По причине полноты пространства R последовательность сходится. Положим , t [0,1]. Тем самым на [0;1] определена функция , к которой сходится поточечно. Осталось доказать, что

1) и 2) при .

С этой целью перейдем в (1) (а точнее, в неравенстве , справедливом при всех t из [0,1]) к пределу при . Получим, что

(2)

В частности, при выполняется оценка:

,

из которой следует ограниченность . Следовательно, . Наконец, формула (2) означает, что . Поэтому при .

.

Пример 2 ( ) – пространство числовых последовательностей , удовлетворяющих условию: , где , ) ­ заданная числовая последовательность; .

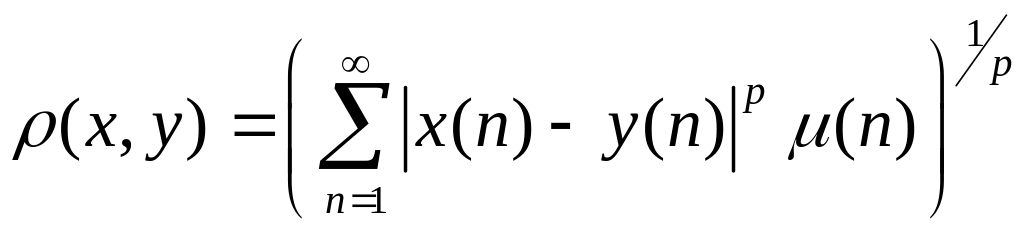Решение. Покажем, что данное пространство полно. Пусть ( ) - фундаментальная последовательность в . Это значит, что

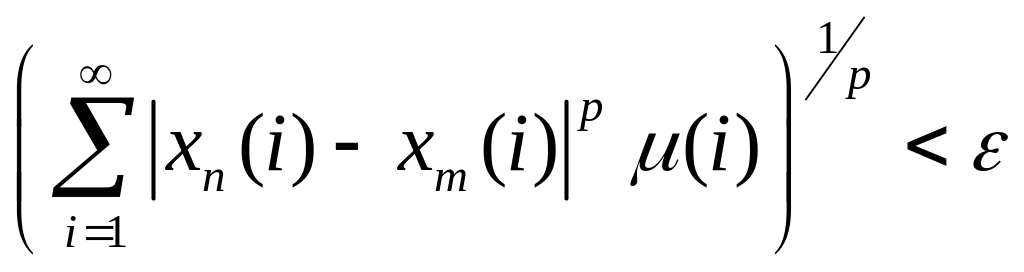: . (1)

Тогда для любого фиксированного имеем , т. е. . Следовательно, для любого фиксированного числовая последовательность является фундаментальной, а потому сходится. Обозначим и положим . Осталось показать, что

1) и

2) при .

Из (1) следует, что любого фиксированного , что в пределе при дает . Переходя теперь к пределу при , получим , т.е.

: (2)

Возьмем какие-нибудь и и обозначим

.

Вследствие неравенства Минковского имеем

,

а это значит, что . Теперь (2) показывает, что при , а потому ( ) сходится в нашем пространстве к .

Пример 3 Х= ­ множество непрерывно дифференцируемых на [-1,1] функций с метрикой .

Решение. Рассмотрим последовательность и покажем, что она является фундаментальной, но не является сходящейся в нашем пространстве. Заметим, что эта последовательность поточечно сходится к функции \ Х., где

.

А так как , то по теореме Лебега при . Это означает, что в пространстве последовательность сходится к . Следовательно, она фундаментальна в Х. С другой стороны, если предположить, что последовательность сходится в данном пространстве Х к некоторой функции , то получим, что имеет два предела в ­ и , ­ противоречие. Итак, данное пространство не является полным.