Самостоятельная работа №6 Задача о кратчайших путях

Необходимо найти кратчайший путь из истока в каждую из остальных вершин графа.

С=

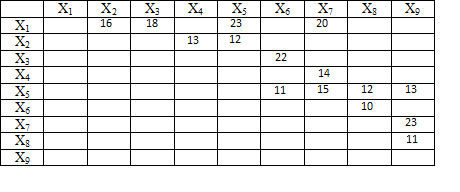
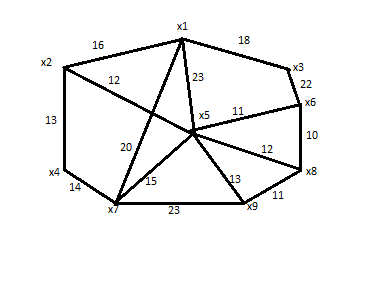
Строим граф по матрице С:

Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х10
0	∞	∞	∞	∞	∞	∞	∞	∞	∞
0			∞	23	∞	6	∞	∞	∞
0	16	18	29		∞		∞	∞	∞
	16	18			40		∞	∞	11
	16				40		15	∞	11
	16						15	10	11
	16						14		11
	16						14
							14

Для вершины х₁ длина кратчайшего пути от S=х₅ оказалась равной 2. Этой вершине могут предшествовать вершины х₃, х₄, х₅:

l(x₃) + C(x₃, x₁) = 9+7 =16

l(x₄) + C(x₄, x₁) = 7+8 =15

l(x₅) + C(x₅, x₁) = 0+2 =2

Сравнивая эти результаты с l(x₁) =2, видим, что в кратчайшем пути вершине х₁ предшествуют вершина х₅.

З апишем это в виде х₅ х₁, l=2.

А налогично получаем х₅ х_2, l=14 (х₅-х₁-х₂₎

х₅ х₃, l=19 (х₅-х₁-х₃₎

х₅ х₄, l=7

х₅ х₆, l=10 (х₅-х₄-х₆₎

х₅ х₇, l=6

х₅ х₈, l=14 (х₅-х₄-х₆-х₈₎

х₅ х₉, l=10 (х₅-х₁-х₃-х₉₎

х₅ х₁₀, l=11 (х₅-х₇-х₁₀₎

Самостоятельная работа №7 Задача о критическом пути в графе

Необходимо построить новый путь от заданной начальной вершины (истока) к заданной конечной вершине (стоку), имеющий наибольшую длину, равную сумме весов дуг, входящих в этот путь.

	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х10
Х1		12	7	8	2
Х2			6						4
Х3				5					1
Х4					7	3		8
Х5							6
Х6							7	4	9	12
Х7										5
Х8									5	4
Х9										6

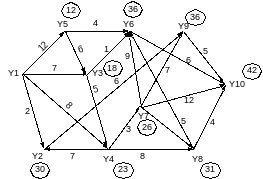
Самый длинный путь от y₁ до:

y ₂ = y₁ y₅ y₃ y₄ y₂ = 12+6+5+7 = 30

y ₃ = y₁ y₅ y₃ = 12+6 = 8

y ₄ = y₁ y₃ y₄ = 18+5 = 23

y ₅ = y₁ y₅ = 12

y ₆ = y₁ y₅ y₃ y₄ y₈ y₆ =12+6+5+8+5 = 36

y ₇ = y₁ y₄ y₇ = 23+3 = 26

y ₈ = y₁ y₄ y₈ = 23+8 = 31

y ₉ = y₁ y₂ y₉ = 30+6 = 36

Критический путь:

y ₁₀ = y₁ y₅ y₃ y₄ y₈ y₆ y₁₀ = 12+6+5+8+5+6 = 42