Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

Владимирский государственный университет им. А.Г. и Н.Г. Столетовых

(ВлГУ)

Кафедра УИТЭС

ОТЧЕТ

по дисциплине

Математическая экономика

5 Вариант

Выполнил:

ст. гр. ПИ-110

Игнатьева Ю.А.

Принял:

Галкин А.А.

Владимир 2012

Самостоятельная работа №1 Задача формализации

Требуется формализовать приведенную ниже задачу.

Производственная мощность цеха сборки некоторого изделия составляет 120 шт. типа и 360 шт. типа в смену. Технический контроль может пропустить в сутки не более 200 изделий того и другого типа. Доход от реализации изделий в 4 раза выше, чем от реализации . Определить план выпуска изделий, при котором будет обеспечена наибольшая прибыль.

Решение:

у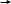 =Р1+4Р2 max

P1<=120

P2<=360

P1+P2<=200

Самостоятельная работа №2 Графическое решение злп

Найти графическим методом решение следующей ЗЛП:

f = 3x₁+x_2, f min

2 x₁+x₂ <=16 (1) x₁ + 2x₂>=8(4)

-7x₁+2x₂ <=14(2) x₁, x₂ >=0

4x₁+6x₂ <=24 (3)

x1	8	0
x2	0	16

2 x₁ +x₂<=16

x1	-2	7
x2	0	0

-7x₁ +2x₂<=14

4x₁ +6x₂<=24

x1	8	0
x2	0	4

x1	6	0
x2	0	4

x₁ +2x₂>=8

Т очка была получена в результате пересечения прямых (3) и (4)

4x₁ +6x₂<=24

x₁ +2x₂>=8

x₁ >=8- 2x₂

4(8- 2x₂) + 6x₂-24<=0

32-8x₂ +6x₂ – 24<=0

8-2x₂ <=0

x₂ <=4

x₁>=8-2x4, x₁>=0

x₁>=0, x₂ =4

y=3x₁ + x₂

y=3x0 + 4=4

Ответ: 4

Самостоятельная работа №3 Симплекс-метод

Преобразовать следующую ЗЛП к канонической форме и решить ее симплекс-методом.

y = x₁-3x₂+x₃ inf

3 x₁-x₂+2x₃ ≤ 1

-2x₁+4x₂ ≤ 12

-4x₁+3x₂+8x₃ ≤ 10

x_i ≥ 0, i = 1,3

ЦФ min

Следовательно, нет необходимости преобразовывать ЦФ.

Приведем условия задачи к каноническому виду.

1-3х₁+х₂-2х₃ ≥ 0

12+2х₁-4х₂ ≥ 0

10+4х₁-3х₂-8х₃ ≥ 0

x_i ≥ 0, i = 1,3

Вводим дополнительные переменные: х₄, х₅, х₆

х ₄ = 1-3х₁+х₂-2х₃

х₅ = 12+2х₁-4х₂

х₆ = 10+4х₁-3х₂-8х₃

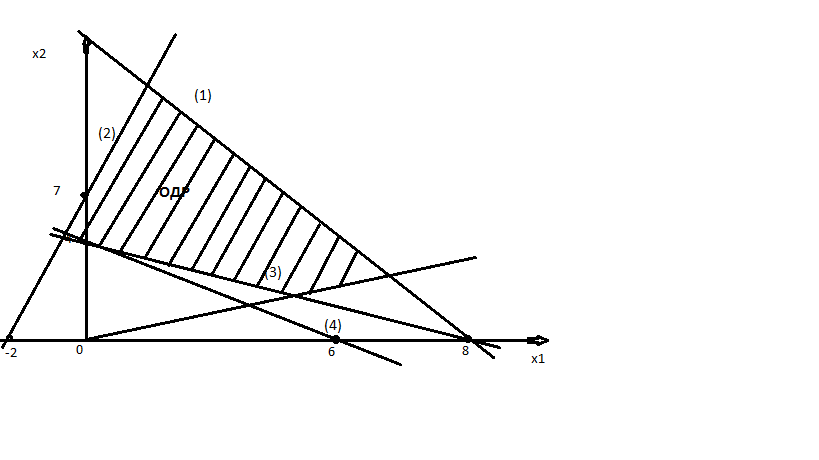
1. Строим симплекс-таблицу.

В строке, соответствующей ЦФ, находим максимальное значение коэффициента при х, равном 4. Столбец, в котором располагается максимальное значение, будем считать ведущим.

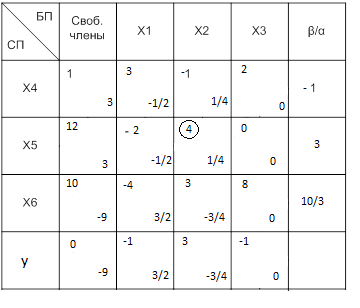
2. Перерисовываем симплекс-таблицу.

Заголовки ведущих строки и столбца меняются местами. Для ведущих строки и столбца в качестве новых значений (верхних левых) берутся нижние правые из первой таблицы. В остальных клетках в качестве новых значений коэффициентов записываются результаты сложения верхнего левого и нижнего правого коэффициентов.

1Повторяем операции, пока в строке, соответствующей ЦФ, все коэффициенты не будут меньше 0 или для единственно оставшегося коэффициента со знаком «+» все α/β не будут меньше 0.

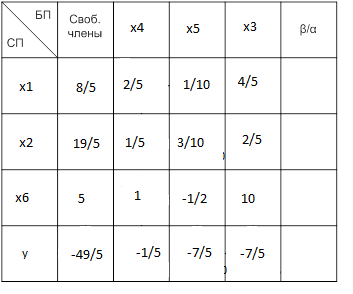
В строке, соответствующей ЦФ, все числа – отрицательные. Следовательно, решение закончено.

х₁ = 8/5 х₅=0

х₂ = 19/5 х₆=5

х₃ = 0

х₄ = 0