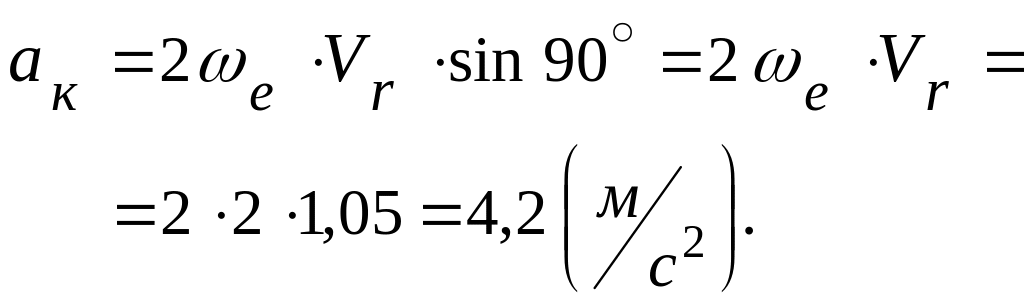3. Сложное движение точки



Вспомни теорию



Абсолютная скорость. Абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей:

.

Здесь  скорость относительного движения,

– скорость переносного движения.

Вычисление относительной скорости . Скорость вычисляется в зависимости от способа задания относительного движения.

А. Движение точки в ее относительном движении задано координатным способом, т.е. в декартовой системе координат задают функции , , тогда:

, .

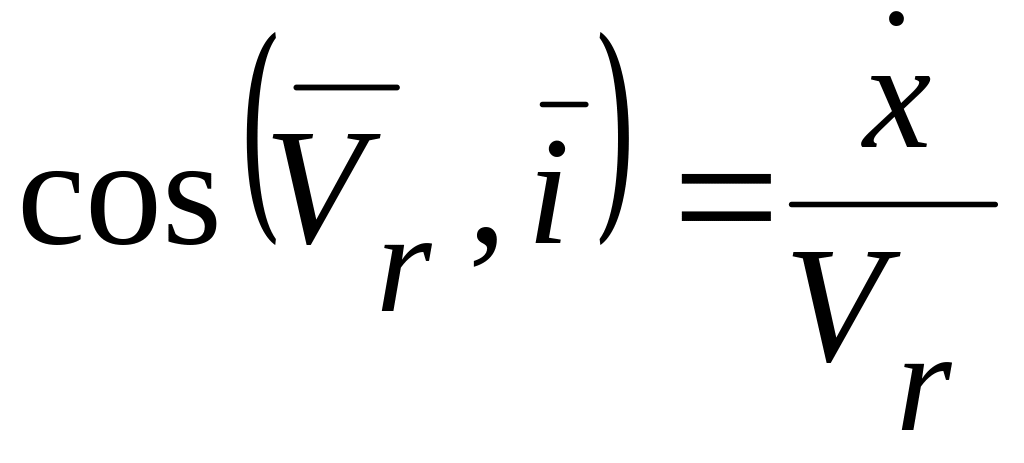Б. Движение точки в ее относительном движении задано естественным способом, т.е. задана траектория движения точки и функциональная зависимость дуговой координаты со временем . Выбирают yнаправление осей естественного трехгранника τ, n.

Тогда:

Вычисление переносной скорости. Рассмотрим частные случаи вычисления переносной скорости.

1. Подвижная система координат движется поступательно со скоростью 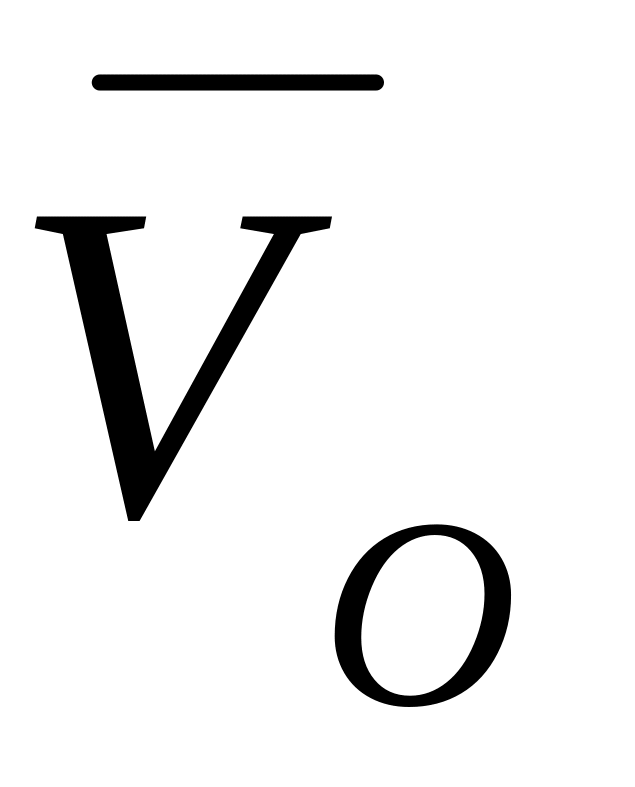. В этом случае 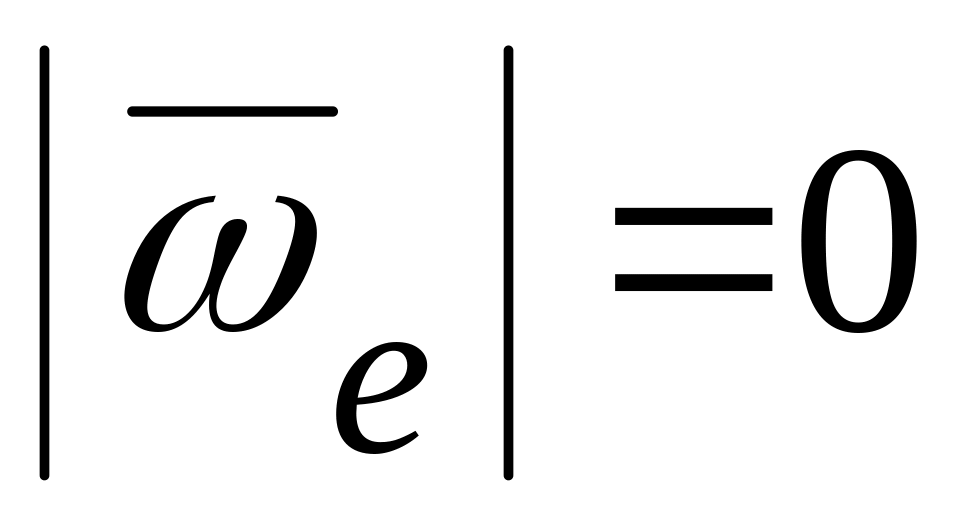и переносная скорость совпадает со скоростью подвижной системы координат, т.е.:

.

2. Подвижная система координат вращается относительно неподвижной оси c угловой скоростью 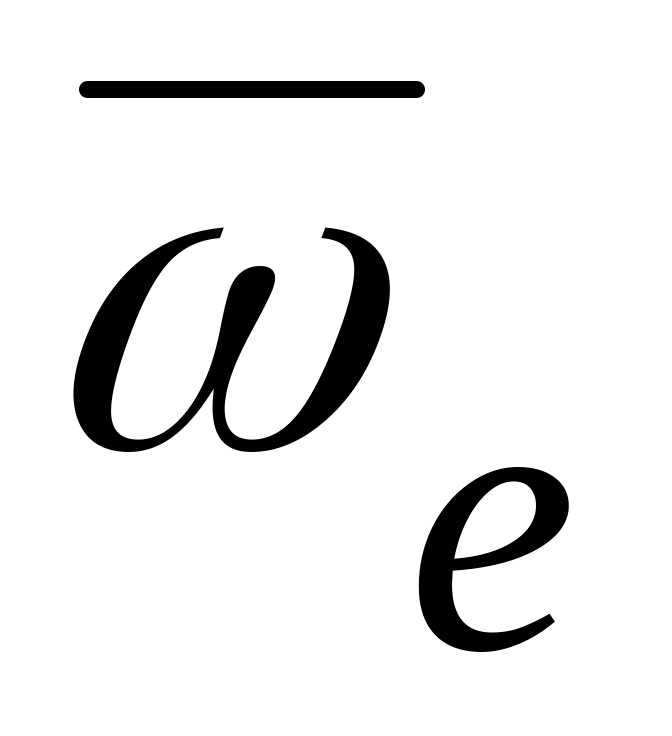. В этом случае , тогда переносная скорость:

.

Абсолютное ускорение. Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса:

.

Здесь: – ускорение относительного движения,

– переносное ускорение,

– ускорение Кориолиса.

Вычисление относительного ускорения. Относительное ускорение вычисляется в зависимости от способа задания относительного движения.

А. При координатном способе задания относительного движения точки М:

; ; .

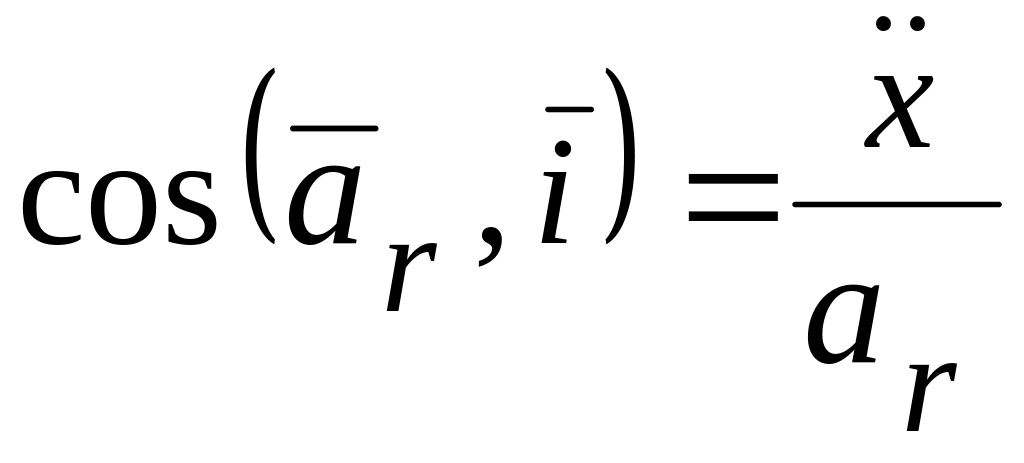Б. При естественном способе задания движения:

, , ,

здесь – радиус кривизны относительной траектории точки М.

Вектор относительного ускорения расположен в соприкасающейся плоскости относительного движения.

Вычисление переносного ускорения. Переносное ускорение вычисляется в зависимости от способа задания относительного движения и движения подвижной системы координат.

А. Подвижная система координат движется поступательно. В этом случае и , следовательно, переносное ускорение точки М:

.

Б. Подвижная система координат вращается относительно неподвижной оси с угловой скоростью и угловым ускорением . В этом случае , тогда переносное ускорение:

Если точка движется по окружности радиусом , то здесь:

Вектор переносного ускорения расположен в соприкасающейся плоскости переносного движения, т.е. в плоскости, перпендикулярной оси вращения.

Вычисление ускорения Кориолиса. Модуль ускорения Кориолиса:

.

Вектор ускорения Кориолиса направлен перпендикулярно вектору угловой скорости , т.е. .

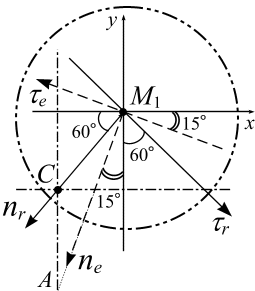
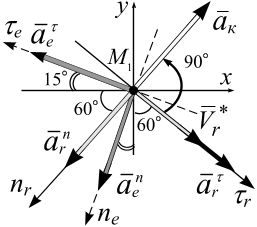
П

Рис. 3.1.

Рис. 3.1

равило Жуковского: чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости на плоскость, перпендикулярную , повернуть на вокруг оси вращения в направлении дуговой стрелки вращения (рис. 3.1).

Задача 3.1. Круглый диск вращается в свой плоскости с постоянной угловой скоростью с^-1 (направление вращения показано на рис. 3.2 дуговой стрелкой). Ось вращения проходит через центр О. По прямолинейному пазу АС движется ползун В согласно заданному уравнению (см) (рис. 3.2, а). Расстояние от центра диска до паза см; см.

Вычислить абсолютную скорость и абсолютное ускорение ползуна В в момент, когда он при движении достигнет середины паза.

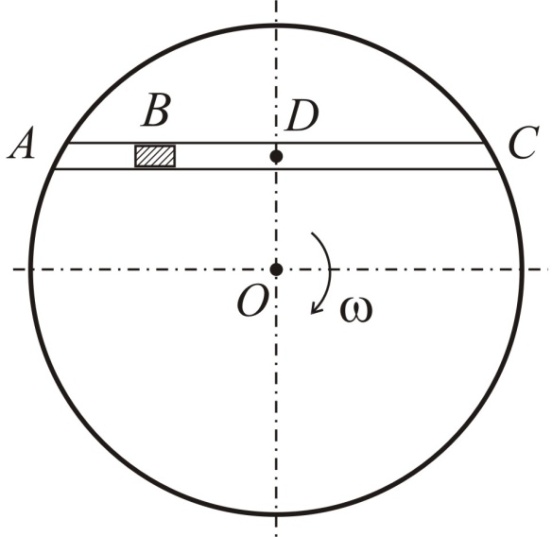
а		б
Рис. 3.2

Решение.

1. Абсолютная скорость ползуна. Абсолютная скорость ползуна при его сложном движении геометрически складывается из относительной и переносной скорости:

.

Относительное движение ползуна. Относительным является прямолинейное движение ползуна В по пазу диска, уравнение относительного движения задано:

.

Относительная скорость ползуна:

(см/с).

В рассматриваемый момент времени ползун находится в середине паза, следовательно, см. Вычислим время, которое соответствует этому положению ползуна, затем модуль относительной скорости в этот момент:

(см) с; (см/с).

На рис. 3.2, б откладываем вектор .

Переносное движение ползуна. Движение ползуна, жестко скрепленного с диском в точке и вращающегося вместе с ним, – переносное движение полз

Рис. 3.3

уна. В переносном движении ползун вращается по окружности радиусом см относительно центра О (рис. 3.2, б). Вводим оси и . Ось совпадает с направлением , ось проходит через центр О. Тогда переносная скорость ползуна В:

(см/с).

Вектор скорости направлен по . Таким образом, векторы и параллельны друг другу и направлены в одну сторону. Соприкасающиеся плоскости относительного и переносного движения совпадают. Поэтому абсолютная скорость точки В вычисляется алгебраическим сложением относительной и переносной скоростей:

(см/с).

2. Абсолютное ускорение ползуна. Абсолютное ускорение ползуна при его сложном движении вычисляется по теореме Кориолиса:

.

Здесь – относительное ускорение ползуна В:

(см/с²) .

Векторы и направлены в одну сторону вдоль оси паза, следовательно, относительное движение ползуна ускоренное (рис. 3.3).

Вычислим переносное ускорение ползуна В  :

Здесь

; (см/с²);

(см/с²).

Вектор направлен по (радиусу переносного вращения) (рис. 3.3).

3. Ускорение Кориолиса. Вектор ускорения Кориолиса равен:

,

модуль ускорения Кориолиса: _.

Соприкасающиеся плоскости относительного и переносного движения совпадают, вектор перпендикулярен плоскости вращения диска, вектор относительной скорости лежит в плоскости вращения диска, поэтому угол между векторами и равен , тогда:

(см/с²).

Направление ускорения Кориолиса определяем по правилу Жуковского: вектор поворачиваем на по направлению дуговой стрелки (рис. 3.3).

Модуль абсолютного ускорения ползуна определяется:

(см/с²).

Направление абсолютного ускорения: .

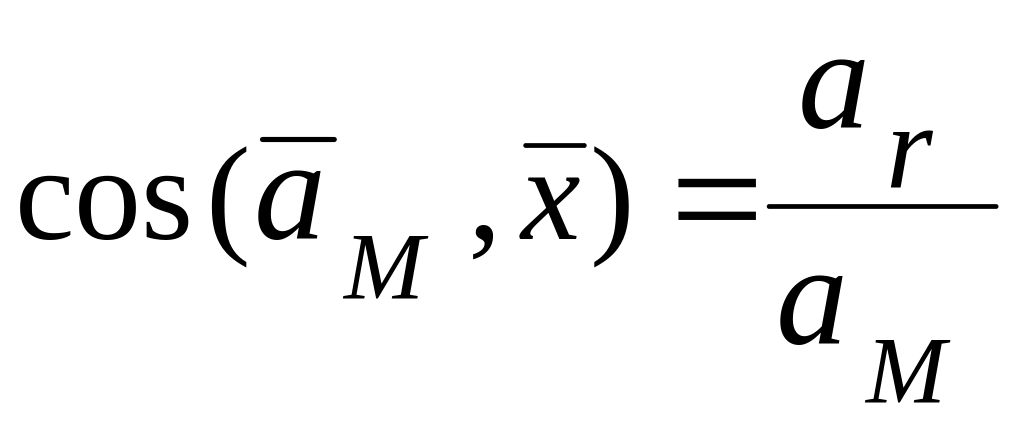Ответ: (см/с); (см/с²).

Задача 3.2. Круглый диск см вращается в свой плоскости относительно неподвижного центра А по уравнению (рад). По ободу диска из точки О в указанном направлении движется точка М согласно заданному уравнению (см) (рис. 3.4, а).

В момент времени с для точки М требуется вычислить абсолютную скорость, абсолютное ускорение.

Решение.

1. Абсолютная скорость точки М.

Абсолютная скорость точки при её сложном движении складывается геометрически из относительной и переносной скоростей:

.

1.1 Относительное движение. Относительным является движение точки М по ободу диска радиусом м. Уравнение относительного движения задано уравнением: .

Относительная скорость:

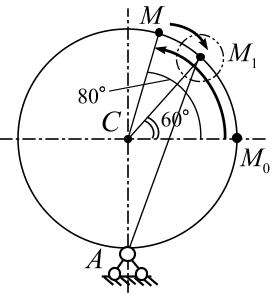
а		б
Рис. 3.4

Проведем анализ движения точки по траектории. При относительная скорость точки положительная, следовательно точка движется от точки (0; 0) по окружности против часовой стрелки до точки , при этом точка проходит путь (рис. 3.4, а):

(см).

Вычислим угол радиус-вектора, который следит за движением точки:

(рад), или .

При скорость , т.е. точка останавливается и далее > движется по часовой стрелке.

Определяем положение точки на диске при с:

(см).

Вычислим угол радиус-вектора при с (рис. 3.4, а):

(рад), или .

Знак модуля при с показывает, что точка движется по окружности по часовой стрелке (рис. 3.5, а). Строим оси и : ось проходит через центр диска (точка С), ось  и направлена по направлению вектора .

1.2. Переносное движение. Переносное движение точки М – движение точки, жестко скрепленной с диском в заданный момент времени (положение точки М при с) и вращающейся вместе с ним. Траекторией движения точки будет окружность радиусом (рис. 3.4, б).

Справка: – равносторонний, поэтому: . Из по теорема косинусов имеем:

Кинематические параметры переносного движения точки М:

(с^-1);

Рис. 3.5

(м/с).

Знак определяет направление вращения диска (рис. 3.5).

Строим оси и : ось проходит через центр вращения диска (точка А), ось  , ось направлена по дуговой стрелке . Вектор скорости направлен по (рис. 3.6, а).

Соприкасающиеся плоскости относительного и переносного движения совпадают (рис. 3.6, а) (ось вращения диска перпендикулярна плоскости рисунка), следовательно, и находятся в одной плоскости  .

Абсолютная скорость точки М определяется (рис. 3.6, б):

, где:

(см/с);

(см/с);

(см/с).

Направление вектора определим по направляющему косинусу:

.

Вектор можно определить графически, как диагональ параллелограмма, построенного на векторах и .

2. Абсолютное ускорение точки М. Абсолютное ускорение точки при ее сложном движении складывается из относительного, переносного ускорения и ускорения Кориолиса:

здесь:  относительное ускорение;

 переносное ускорение;

 ускорение Кориолиса.

2.1. Относительное ускорение точки М:

, где:

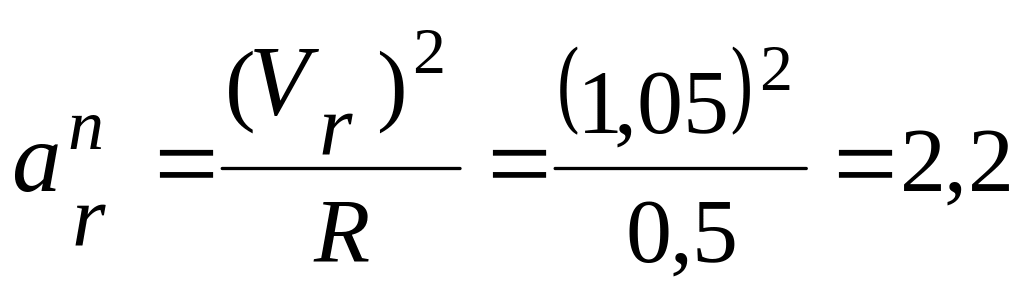(м/с²).

Векторы и направлены в одну сторону по , т.к. и _; следовательно, относительное движение точки ускоренное (рис. 3.6, б, в). Вектор направлен по оси .

2.2. Переносное ускорение точки М.

Угловое ускорение пластины:

а		(с-2), т.к. , , вращение диска – равнозамедленное, дуговые стрелки и направлены в разные стороны (рис. 3.5). Вектор переносного ускорения: , где: Вектор направлен по , вектор  по (рис. 3.6, в). 2.3. Ускорение Кориолиса: , или , т.к. соприкасающиеся плоскости переносного и относительного движений совпадают, вектор перпендикулярен плоскости вращения, имеем: Направление ускорения Кориолиса определяем по правилу Жуковского:
б
в
Рис. 3.6

вектор поворачиваем на по направлению дуговой стрелки (рис. 3.6, в).

2.4. Абсолютное ускорение точки М:

,

здесь:

(см/с²);

(см/с²);

(м/с²).

Направление абсолютного ускорения:

.

Ответ: (м/с); (м/с²).

Задача 3.3. Фигурная пластина вращается по заданному уравнению (рад) относительно неподвижной горизонтальной оси. По диагонали пластины из точки О движется точка М согласно заданному уравнению (см). Размеры пластины см, см (рис. 3.7).

Рис. 3.7

В момент времени с для точки М требуется:

1. Вычислить абсолютную скорость, показать геометрически направление векторов относительной, переносной и абсолютной скорости.

2. Вычислить абсолютное ускорение, показать геометрически направление векторов относительного, переносного ускорения и ускорения Кориолиса.

Решение.

1. Вычислим абсолютную скорость точки М.

Абсолютная скорость точки при ее сложном движении складывается из векторов относительной и переносной скорости:

.

1.1. Относительным является движение точки М по диагонали прямоугольной пластины, оно задано уравнением . Определим положение точки М на диагонали пластины:

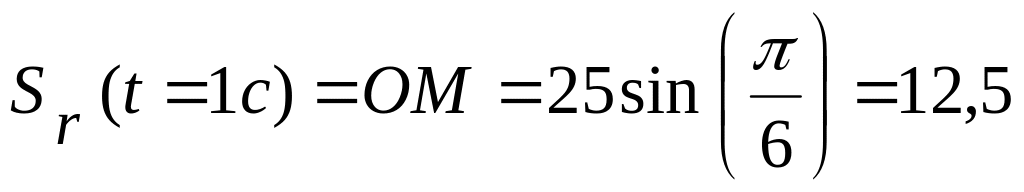см.

Относительная скорость точки: ;

(см/с).

Относительное движение точки М прямолинейное вверх (рис. 3.8, а), вектор направлен вдоль диагонали пластины по ходу относительного движения, т.к. .

а		б
Рис. 3.8
Справка. Из геометрии пластины: (см); (см); (см). ; (см).

Переносное движение точки М криволинейное, т.к. пластина вращается относительно оси по окружности радиусом (рис. 3.8,б).

Параметры переносного движения:

(с^-1); (с^-2).

Знак определяет направление вращения пластины по часовой стрелке, и вектор скорости строится в указанном направлении переносного вращения (рис. 3.8, б). Модуль переносной скорости:

(см/с);

Плоскости относительного и переносного движения в данной задаче взаимно перпендикулярны, следовательно . Тогда модуль абсолютной скорости точки М рассчитывается так:

(см/с).

2. Рассчитываем абсолютное ускорение точки М.

Абсолютное ускорение точки при ее сложном движении геометрически складывается из относительного, переносного ускорения и ускорения Кориолиса:

.

2.1. Относительное ускорение:

(см/с²).

Векторы и направлены вдоль диагонали пластины в противоположные стороны, т.к. , ; следовательно, относительное движение точки замедленное (рис. 3.7, а).

2.2. Переносное ускорение.

Угловое ускорение пластины (переносное угловое ускорение точки):

(с^-2),

т.к. , переносное вращение относительно оси ускоренное по часовой стрелке (рис. 3.8, б).

Модули векторов переносного ускорения точки М (рис. 3.8, б):

(см/с²); (см/с²).

2.3. Ускорение Кориолиса:

, или ,

где (рис. 3.8, б);

(см/с²).

Вектор ускорения Кориолиса получаем поворотом вектора на в направлении , т.е. по часовой стрелке, в соприкасающейся плоскости переносного движения (рис. 3.8, б).

Строим векторы переносного ускорения и ускорения Кориолиса в соприкасающейся плоскости переносного движения  плоскости .

Плоскости относительного и переносного движения взаимно перпендикулярны, тогда абсолютное ускорение точки М рассчитывается по формуле:

.

С учетом расположения векторов, входящих в теорему, в двух соприкасающихся плоскостях , (рис. 3.8, а,б), расписываем проекции векторов на указанные оси:

(см/с²);

(см/с²);

(см/с²);

(см/с²).

Ответ: (см/с); (см/с²).

!!! Алгоритм решения

Заданы уравнения относительного и переносного движения ; требуется вычислить скорость абсолютного движения:

• раскладываем абсолютное движение точки на два составных движения  переносное и относительное;

• выбираем две системы координат: абсолютную, условно принимаемую неподвижной, и относительную, которую связываем с движущимся телом;

• составляем уравнения относительного движения точки и уравнения переносного движения точки;

• мысленно остановив переносное движение, вычисляем скорость и ускорение точки в относительном движении;

• мысленно остановив относительное движение, вычисляем угловую скорость переносного движения 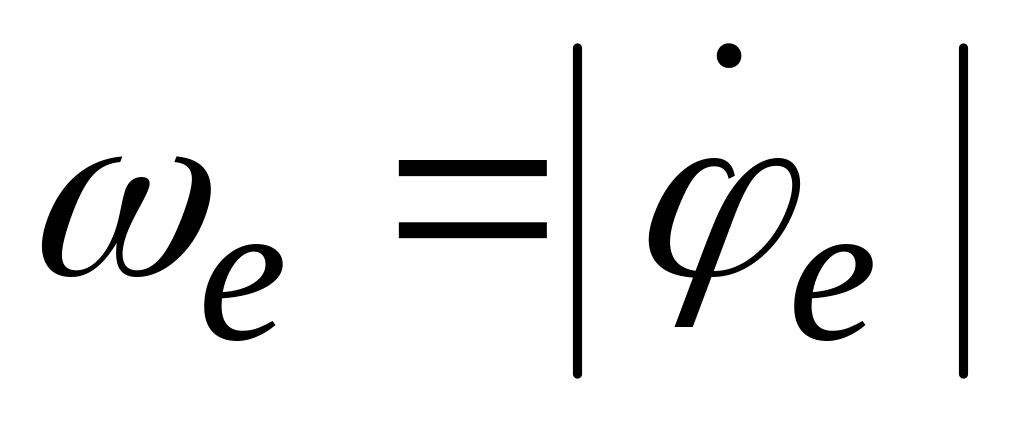и угловое ускорение точки в переносном движении ;

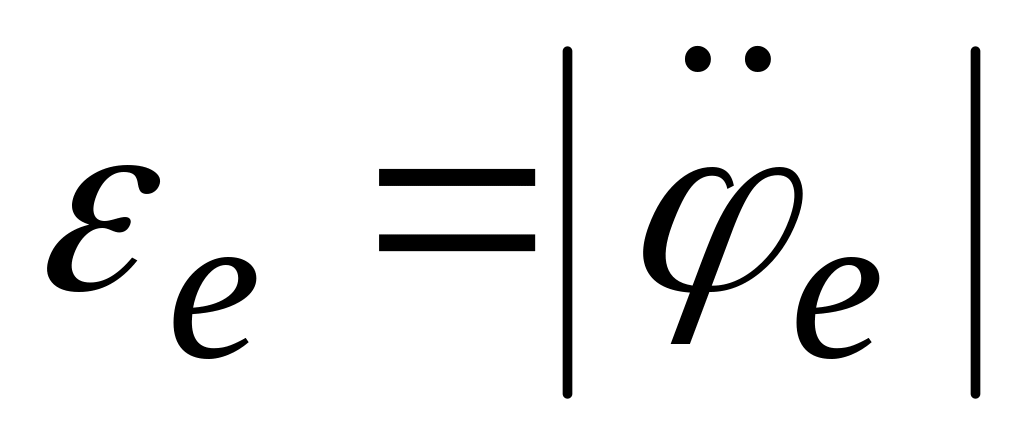• по известным угловой скорости переносного движения и скорости в относительном движении, используя правило Жуковского, вычисляем ускорение Кориолиса точки ;

• пользуясь методом проекций, вычисляем проекции абсолютной скорости и абсолютного ускорения точки на оси координат;

• по вычисленным проекциям абсолютной скорости и абсолютного ускорения находим искомую абсолютную скорость и абсолютное ускорение по модулю и направлению.

		Задачи для самостоятельного решения
					1. Полое кольцо радиусом см вращается в своей плоскости относительно центра О в указанном направлении с постоянным угловым ускорением (с-1). По кольцу из центра О в указанном направлении движется точка М по уравнению (см). Вычислить абсолютное ускорение точки М в момент, когда она достигнет положения С.
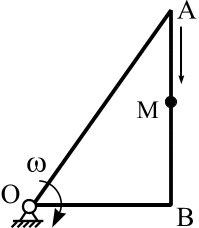
			2. Прямоугольный треугольник ОАВ вращается с постоянной угловой скоростью с-1 в своей плоскости вокруг оси, проходящей через вершину О. Точка М движется с постоянным ускорением см/с2 вдоль стороны треугольника от А к В. Вычислить абсолютные скорость и ускорение точки М в момент времени с, считая, что в этот момент треугольник ОАВ занимает положение, указанное на чертеже и см, (начальная скорость точки М равна нулю).
3. По радиусу диска, вращающегося вокруг оси с угловой скоростью (рад/с), в направлении от центра диска к его ободу движется точка согласно уравнению (см). Радиус составляет с осью угол 60. Вычислить величину абсолютного ускорения точки в момент с.
	4. Прямоугольник вращается вокруг стороны с угловой скоростью (с-1). Вдоль стороны движется точка по закону (м). Даны размеры: (м), . Вычислить величину абсолютного ускорения точки в момент времени 1 с.
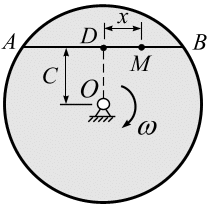
				5. Диск вращается с постоянной угловой скоростью вокруг оси, проходящей через его центр перпендикулярно плоскости диска. По хорде из ее середины движется точка , согласно уравнению движения (см). Хорда отстоит от центра диска на расстояние . Вычислить абсолютную скорость и абсолютное ускорение точки .
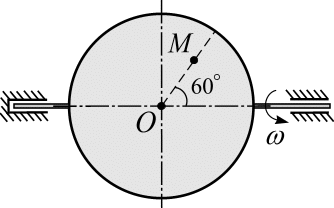
				6. Шарик движется с постоянной скоростью (м/с) от точки к точке по хорде диска . Круг вращается замедленно вокруг оси, которая проходит через его центр перпендикулярно плоскости диска. Вычислить абсолютное ускорение шарика, когда он находится на кратчайшем расстоянии от центра диска, равном 30 см. В этот момент угловая скорость диска (с-1), угловое ускорение (с-2).
7. По кольцу радиусом м из точки О движется точка М согласно уравнению (м). Кольцо вращается вокруг горизонтальной оси . Вращение кольца задано уравнением (рад). Вычислить абсолютную скорость и абсолютное ускорение точки М в момент времени с.