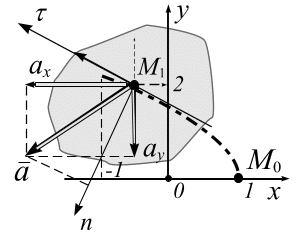
1.3. Естественный способ задания движения точки



Вспомни теорию



П

Рис. 1.16

ри естественном способе задания движения точки известно (рис. 1.16):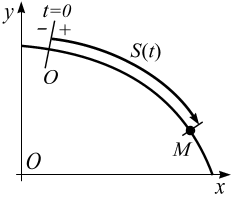

• траектория точки;

• начало и направление движения, т.е. направление увеличения дуговой координаты;

• уравнение движения где S – дуговая координата.

Скорость и ускорение точки. При естественном способе задания движения точки в плоскости применяют оси естественного трехгранника , , которые жестко связываются с точкой М и движутся вместе с ней. Плоскость , называется соприкасающейся плоскостью.

Скорость точки. Вектор скорости направлен по оси и вычисляется:

Ускорение точки. Вектор ускорения раскладывается на два вектора и (рис. 1.17):

.

Здесь: вектор – определяет касательную составляющую ускорения . Модуль касательного ускорения показывает изменение модуля скорости. Вектор при направлен в сторону вектора (ускоренное движение) (рис. 1.17, а), а при – против вектора (замедленное движение) (рис. 1.17, б);

а

б

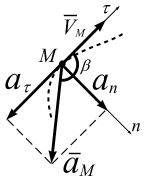
Рис. 1.17

• вектор ( – радиус кривизны траектории) – определяет нормальную составляющую ускорения. Модуль нормального ускорения определяет изменение направления вектора скорости . При прямолинейном движении = , , вектор при движении не меняет направление. При криволинейном движении точки нормальная составляющая ускорения всегда направлена внутрь вогнутости траектории вдоль оси (рис. 1.17).

Учитывая ортогональность и , имеем:

, .

Связь координатного и естественного способов заданий движения точки. Уравнение движения в естественной форме связано с уравнениями движения в координатной форме соотношением:

.

З десь , . Тогда:

;

; .

Радиус кривизны может быть вычислен через модуль скорости и модуль нормального ускорения: .

Задача 1.7. Движение точки М задано уравнением:

(м). (а)

Вычислить путь , пройденный точкой М за 10 с.

Решение. Путь, пройденный точкой, вычислим по интегральной зависимости:

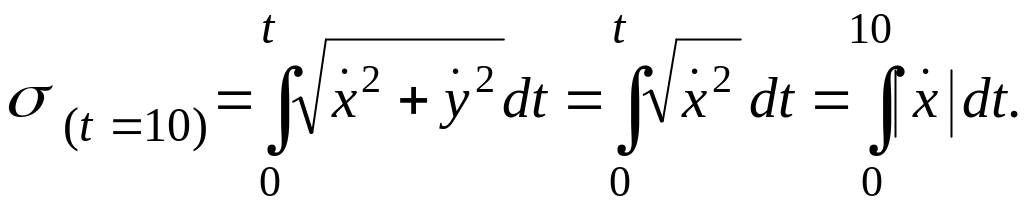
Согласно уравнению движения (а), имеем:

.

При с точка М меняет свое направление, поэтому путь , пройденный точкой за 10 с, будет вычисляться так:

(м).

Ответ: (м).

Задача 1.8. Движение точки в плоскости задано координатным способом уравнениями , :

	(а)
	(б)

где и выражены в см,  в с.

Требуется задать движение точки в явном виде; вычислить скорость, нормальную и касательную составляющие ускорения, радиус кривизны траектории в соответствующей точке для момента времени с.

Решение. Для построения траектории в декартовой системе координат определим область значений и . Функции и  ограничены, тогда область значений и определяетя неравенствами:

; .

Получим зависимость . Для этого из (а)–(б) исключим параметр . Введём обозначение , тогда уравнения (а) и (б) перепишутся в виде:

Распишем первое уравнение полученной системы, используя формулу двойного угла ( ), приведем подобные члены и выразим через :

.

И

Рис. 1.18

так, координаты связаны между собой зависимостью

.

Анализируем траекторию движения точки. Траекторией точки является парабола с координатой вершины , ветви параболы вытянуты вдоль оси слева от вершины (рис. 1.18).

При функция убывает, а  возрастает (рис.1.18); следовательно, точка из положения начинает движение по верхней ветви параболы до точки , далее точка движется обратно по верхней ветви траектории и через точку с координатами движется по нижней ветви параболы до точки – и т.д.

В целом точка М совершает колебательные движения по построенной параболе в ограниченной пунктиром области. Направление движения в первые 2 с указано стрелкой на рис. 1.18.

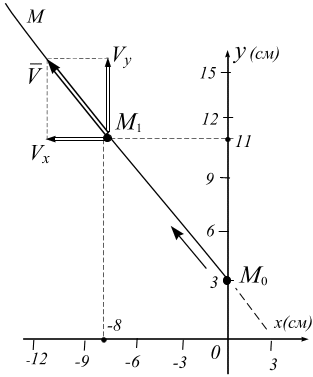
Вычислим положение точки на траектории при с:

(см);

(см).

а

б

Рис. 1.19

2. Вычислим скорость точки при с.

(см/с);

(см/с);

(см/с).

Cправка. Формулы приведения: ; .

Значения и отложим в масштабе на графике (рис. 1.19, а). Вектор скорости точки является диагональю параллелограмма, достроенного на этих векторах, и определяет направление движения точки, а также определяет направление и положение касательной оси .

Вычислим ускорение точки при с:

(см/с²);

(см/с²);

(см/с²).

Вектор ускорения точки –  получаем построением параллелограмма на проекциях ускорений и в выбранном масштабе (рис. 1.19, б).

Как видно из рис. 1.19, в вектор полного ускорения точки направлен внутрь вогнутости траектории движения точки.

Касательная и нормальная составляющие ускорения точки. При координатном способе задания движения указанные составляющие ускорения рассчитываются по формулам:

(см/с²);

(см/с²).

Касательное и нормальное ускорения точки можно вычислить геометрически. Для этого в точке необходимо построить оси естественного трехгранника и . Положение и направление оси определили ранее  по построенному вектору скорости точки . Перпендикулярно этой оси, в сторону в

Рис. 1.20

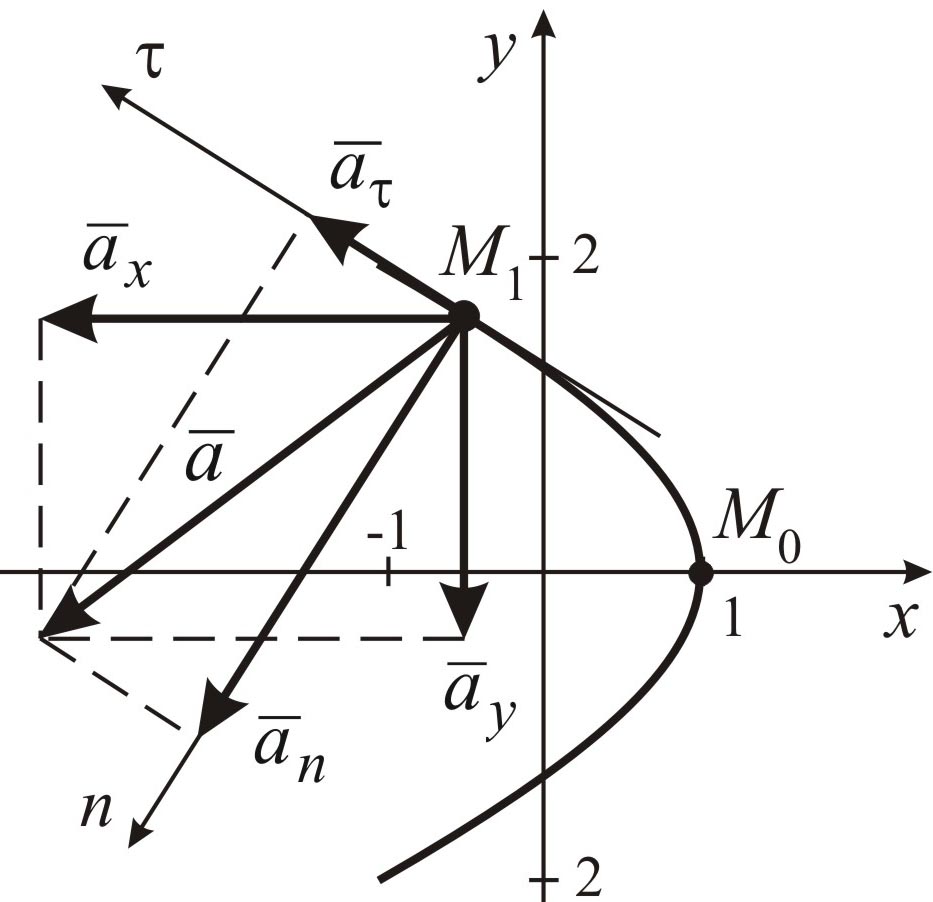
огнутости траектории, проведём главную нормаль (полуось). Отложим в масштабе проекции и и построим вектор (рис. 1.20).

Проекция вектора ускорения на ось будет соответствовать касательной составляющей ускорения . Измеряя длину указанного вектора и умножая на масштаб, получим значение ; в данном случае (см/с²). Вектор совпадает по направлению с вектором скорости точки , следовательно, движение точки по параболе в данный момент времени – ускоренное.

Соответственно, проекция на ось будет определять нормальное ускорение . Измеряя длину полученной проекции и умножая на масштаб, получим значение ; в данном случае (см/с²).

Получено достаточно хорошее соответствие значений и , рассчитанных разными способами.

Радиус кривизны траектории.

Вычисим радиус кривизны траектории. Имеем:

_{откуда:} (см).

Вычислим уравнение движения точки, заданное естественном способом – .

Имеем:

.

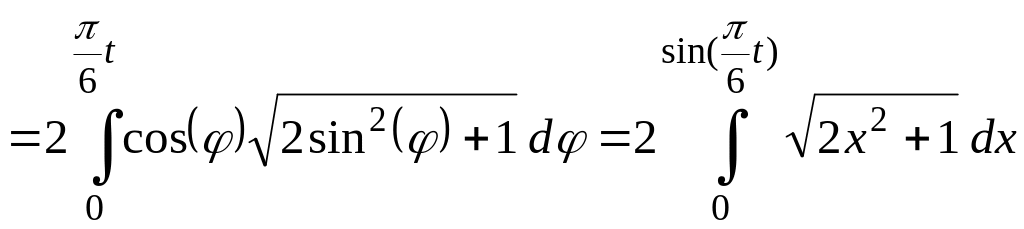Получили уравнение движения точки, заданное естественным способом в интегральном виде.

Ответ: уравнение траектории точки в явном виде ; скорость точки (см/с); ускорения точки (см/с²), (см/с²), (см/с²); радиус кривизны траектории см; .

Задача 1.9. Движение точки в плоскости задано координатным способом уравнениями:

(см), (а)

(см). (б)

Требуется задать движение точки в явном виде, вычислить скорость, нормальную и касательную составляющие ускорения, радиус кривизны траектории в соответствующей точке для момента времени с.

Решение. Для построения траектории в декартовой системе координат определим область значений и . Имеем из (а) и (б):

, . (с)

Уравнения движения точки (а)–(б) заданы параметрически, т.е. координаты x и y зависят от параметра . Чтобы записать уравнение траектории в декартовой системе координат, из заданных уравнений необходимо исключить параметр .

Из (а) получаем , подставляем в (б):

.

Таким образом, получили уравнение траектории:

.

Рис. 1.21

Траекторией движения точки является отрезок прямой, распложенной в области , . Движение точки прямолинейное. Строим траекторию. Для этого достаточно знать координаты двух точек: при , (см); при , (см). При точка из начального положения начинает движение по отрезку (рис. 1.21). Направление движения отмечено стрелкой на траектории. При (с): (см), (см).

Обозначим положение точки при (с) через , рис. 1.21.

Скорость и ускорения точки при с:

(см/с), (см/с).

Значение скорости точки не зависит от времени , т.е. точка движется с постоянной скоростью:

(см/с).

Полученные значения и отложим на графике (рис. 1.21) в масштабе. Вектор скорости точки является диагональю параллелограмма, достроенного на значениях и .

Ускорение точки при с:

, ; .

Прямолинейное движение точки является равномерным.

При прямолинейном движении нормальное ускорение .

Радиус кривизны траектории:

.

Вычислим уравнения движения при естественном способе :

.

Ответ: уравнение траектории в декартовой системе координат: ; скорость точки (см/с); ускорения точки , , ; радиус кривизны траектории ; .

!!! Алгоритм решения

Первый тип задач (прямая задача) – заданы уравнения движения точки в плоскости , или , требуется вычислить скорость и ускорение точки тела; если движение точки задано координатным способом  то вычислить уравнение траектории в явном виде .

Схема решения:

• выбирают систему координат ( или ) и начало координат (та или иная система выбираются исходя из условий задачи так, чтобы дальнейшее решение было по возможности более простым);

• на основании условий задачи для избранной системы координат составляют уравнения движения точки (если они явно не заданы), т.е. находят зависимости координат точки от времени – , ;

• исключая параметр из уравнений движения, вычисляют траекторию точки как функцию – ;

• дифференцируя по времени уравнения движения , , или , вычисляют скорость точки;

• вычисляя вторую производную по времени от , , находят ускорение точки;

• если движение точки задано естественным способом, т.е. задана траектория движения, радиус кривизны и , вычисляют нормальную и касательную составляющие ускорения;

• вычисляют полное ускорение точек по модулю и направлению.

Второй тип задач (обратная задача)  заданы проекции ускорения , ; требуется вычислить проекции скорости точки, как функцию времени, т.е. и вычислить уравнения движения точки в декартовой системе координат, т.е. , .

Схема решения:

• выбирают систему координат;

• формулируют начальные условия задачи: ;

• разделяют переменные в дифференциальных уравнениях и , или , и, интегрируя по времени дифференциальные уравнения с разделенными переменными, вычисляют проекции скорости точки , , а также уравнения движения точки , .

	Задачи для самостоятельного решения
			1. Положение линейки АВ определяется углом (рад). Вычислить проекцию скорости точки М на ось Ох в момент времени с, если расстояние м.
					2. Положение кривошипа определяется углом (рад). Вычислить скорость и ускорение ползуна В в момент времени с, если м.
3. Точка движется по прямой с ускорением (м/с2). Вычислить начальную скорость точки, если через 6 с скорость точки составила 3 м/с.
4. Проекция скорости точки . Вычислить координату х точки в момент времени с, если в момент времени координата м.
5.Точка движется по прямой с ускорением (м/с2). Вычислить начальную скорость точки, если через 2 с скорость точки составила 6 м/с.
6. Движение точки задано уравнениями и . Вычислить касательное ускорение в момент времени с.
7. По заданному уравнению движения точки на произвольно выбранной траектории построить через равные промежутки времени шесть положений точки, определить расстояние по траектории от начала отсчета до конечного положения точки и пройденный ею путь за указанный промежуток времени ( и  в сантиметрах, t  в секундах):
, . , . , .
8. По заданным уравнениям движения точки найти уравнения ее траектории в координатной форме и указать на рисунке направление движения: , . , . , . , .
9. Снаряд движется в вертикальной плоскости согласно уравнениям , (t – в секундах, х и у – в метрах). Вычислить: скорость и ускорение в начальный момент; высоту и дальность обстрела; радиус кривизны траектории в наивысшей точке.
				10. Вычислить ускорение точки В в момент времени, когда угол , если длина см, а закон изменения угла (рад).
		11. Положение кривошипа ОА определяется углом (рад). Вычислить проекции ускорения , точки А в момент времени с, если длина кривошипа м.
				12. Положение линейки АВ определяется углом (рад). Вычислить проекции ускорения точки М на оси и в момент времени с, если расстояние м.
13. Точка движется по прямой Ох с ускорением . Вычислить координату х точки в момент времени с, если при скорость км/ч, и координата .
14. Касательное ускорение точки . Определить момент времени t, когда скорость точки достигнет 10 м/с, если при скорость м/с.
15. Проекции скорости точки во время движения определяются выражениями , м/с. Вычислить касательное ускорение в момент времени с.
16. Даны уравнения движения снаряда: , , где  начальная скорость снаряда, – угол между и горизонтальной осью х; g – ускорение силы тяжести. Определить траекторию движения снаряда, высоту Н, дальность L и время Т полета самолета.
						17. Из орудия береговой артиллерии с высоты м над уровнем моря произведен выстрел под углом к горизонту, начальная скорость снаряда м/с. Вычислить, на каком расстоянии от орудия снаряд попадет в цель, находящуюся на уровне моря. Уравнения движения снаряда в вертикальной плоскости: , .