1Жидкости. В природе различают четыре вида состояния вещества: твердое, жидкое, газообразное и плазменное. Основное отличие жидкостей от твердых тел заключается в их текучести, т.е. способности легко принимать форму сосуда, в который жидкость поместили, при этом объем жидкости не изменяется. Газ тоже обладает текучестью, но при этом занимает любой предоставленный ему объем. В сосудах жидкость образует свободную поверхность, а газ аналогичной поверхностью не обладает. Однако с точки зрения механики и жидкость, и газ подчиняются одним и тем же закономерностям в случае, если сжимаемостью газа можно пренебречь. Поэтому в гидравлике под термином «жидкость» понимаются и собственно жидкости (которые часто называют капельными жидкостями), и газы (газообразные жидкости).

Основные свойства жидкости (при рассмотрении задач механики жидкости) — это плотность, способность изменять свой объем при нагревании (охлаждении) и изменениях давления, вязкость жидкости. Рассмотрим каждое из свойств жидкости подробнее.

Плотность жидкости. Плотностью жидкости ρ называется ее масса, заключенная в единице объема:

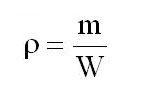
2 Истечение из малых отверстий в тонкой стенке сосуда

Отверстие можно считать малым, если его высота меньше одной десятой части напора, под которым происходит истечение. Скорость вытекания жидкости из открытого сосуда через отверстие определяют по формуле , где H и Dp – напор и избыточное давление в центре отверстия; j – коэффициент скорости, учитывающий потери напора, обусловленные протеканием жидкости через отверстие. При истечении из закрытого сосуда с давлением р на поверхности жидкости в среду с давлением ро скорость истечения находят по формуле . Расход жидкости, вытекающей из отверстия равен: , где e – коэффициент сжатия струи; Sо – площадь сечения отверстия; m – коэффициент расхода отверстия. Число Рейнольдса при истечении из отверстий определяют по скорости истечения, т.е. для истечения из открытого сосуда оно имеет вид . При истечении с большими значениями числа Рейнольдса (ReH>100000) можно принимать следующие значения коэффициентов истечения: e = 0,62 – 0,63; j =  0,97 – 0,98; m = 0,61. При истечении с малыми числами Рейнольдса все коэффициенты истечения зависят от значений ReH. Для определения коэффициента расхода используют приближенные формулы: при ReH < 25 ; при 25 < ReH < 300 ; при 300 < ReH < 10000 ; при ReH > 10000 . При истечении жидкостей с малой вязкостью через отверстия малого диаметра и при небольших напорах на коэффициент расхода оказывает влияние поверхностное натяжение.

Истечение из насадков и коротких труб

Короткую трубку  , присоединенную к отверстию для изменения характеристик истечения, называют насадком. Формула расхода для насадков та же, что и для отверстий в тонкой стенке. Отличие в расходе учитывают с помощью коэффициента расхода насадка mн. Для насадков разных типов в автомодельной относительно числа Рейнольдса области истечения значения коэффициентов расхода приведены в приложении П 1.11. При истечении из коротких трубопроводов следует учитывать не только местные сопротивления, но и потери на трение. При этом расчетная зависимость имеет вид , где   – коэффициент расхода системы (при истечении под уровень –  ).

Истечение при переменном напоре

Истечение при переменном напоре обычно имеет место при опорожнении или наполнении резервуаров. Дифференциальное уравнение процесса опорожнения открытого резервуара произвольной формы при отсутствии притока в него жидкости имеет вид , где Sz – площадь свободной поверхности жидкости в резервуаре (в общем случае зависит от вертикальной координаты z); dz – понижение уровня жидкости за время dt; Qz – расход жидкости через выпускное отверстие. Истечение жидкости под действием переменного напора является неустановившимся, однако, если площадь поперечного сечения резервуара достаточно велика по сравнению с площадью выходного отверстия, то переменная скорость опускания уровня жидкости будет весьма малой. В этом случае локальными ускорениями частиц жидкости можно пренебречь, рассматривать процесс истечения за бесконечно малый промежуток времени как установившийся. Мгновенный расход при этих условиях определяется по формуле , где m – коэффициент расхода выпускного устройства, отнесенный к площади Sо выходного отверстия. При квадратичном режиме истечения коэффициент расхода можно принимать постоянным в течение всего процесса. Тогда для резервуара с постоянной по высоте площадью поперечного сечения время частичного опорожнения сосуда от начального уровня Ho до произвольного уровня H находят по формуле . Коэффициент расхода m выпускного устройства определяется его конструкцией. Время полного опорожнения резервуара при переменном напоре в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном начальному уровню Ho. При истечении жидкостей с большой вязкостью (ReH < 10) время опорожнения рассчитывают по формуле , где S – площадь горизонтального сечения резервуара, n – кинематическая вязкость жидкости.

где m — масса жидкости; W — объем жидкости.

Единица измерения плотности — кг/м³.

Так как вода является наиболее распространенной в природе жидкостью, в качестве примера количественного значения параметра, определяющего то или иное свойство жидкости, будем приводить значение рассматриваемого параметра для воды.

Плотность воды при 4 °С ρ_в = 1000 кг/м³. Плотность жидкости уменьшается при увеличении температуры. Однако для воды эта закономерность справедлива только с 4 °С, в чем проявляется одно из аномальных свойств воды.

Удельный вес. Удельный вес γ — это вес жидкости, приходящийся на единицу объема:

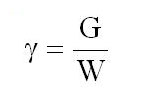
где G — вес жидкости в объеме W.

Единица измерения удельного веса — Н/м³.

Удельный вес воды при температуре 4 °С γ_в= 9810 Н/м³.

Плотность и удельный вес связаны между собой соотношением

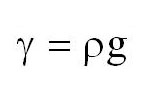
где g — ускорение свободного падения (g=9,81 м/с²).

Вообще плотность и удельный вес отичаются лиш тем, что у плотности сила веса измеряется в килограммах, а у удельного веса в ньютонах. Килограммы легко переводятся в ньютоны и обратно. Вообще эти параметры нам помогут вычислять массу в любых объемах.

Температурное расширение. Это свойство жидкости характеризуется изменением объема при изменении температуры, которое определяется температурным коэффициентом объемного расширения жидкости β_t:

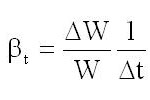
где W - начальный объем жидкости; ΔW - Изменение объема после уменьшения или увеличения температуры; Δt - изменение температуры.

Знак Δ означает разницу между начальной величиной и конечной величиной. То есть ΔW=Wконечный-Wначальный

Единица измерения β_t; — град^-1,

для воды,при t=20 °С β_t = 0,00015 [1/°С].

Это свойство нужно обязательно знать! В будущем нам придется вычислять количество жидкости которое будет увеличиваться в замкнутой системе отопления. И при этом мы сможем посчитать на сколько литров нам необходим раширительный бак для системы отопления.

Получается, что этот параметр β_t показывает изменение величины объема на единицу температуры. То есть, если температура изменилась на 10 градусов, то объем увеличится в 10раз от величины β_t.

Сжимаемость. Это свойство жидкости менять свой объем при изменении давления, которое характеризуется коэффициентом объемного сжатия β_p :

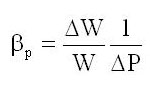
где W - начальный объем жидкости; ΔW - изменение объема после изменения давления; ΔP - изменение давления.

Единица измерения β_p - Па^-1 Коэффициент объемного сжатия капельных жидкостей мало меняется в зависимости от давления и температуры.

Для воды β_p = 5×10^-10 Па^-1

Вы только не путайте давление с плотностью. Так как буквы похожи, я и сам сначало об этом подумал. О давлении будет рассказано в следующих статьях. Вообще я сейчас не рекомендую вникать в понятие сжимаемость, так как вы возможно незнакомы с понятием давления и поэтому возможно несможите понять связь.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости Е и определяется по формуле:

для воды E=2×10⁹ Па.

Вязкость жидкости — свойство жидкостей оказывать сопротивление сдвигу. Это свойство проявляется только при движении жидкостей. Вязкость характеризует степень текучести жидкости. Наряду с легко подвижными жидкостями (вода, спирт, воздух и др.) существуют очень вязкие жидкости (глицерин, машинные масла и др.).

Я предлогаю понять вязкость следующем образом: Представте жидкое вещество ввиде находящихся в ней большого количество мелких шариков, атомов, малекул, кому как угодно. И представте, что их начинает ктото толкать. И во время толкания шарики начинают терется друг об друга сопротивляясь перемещению. Дык вот, а теперь представим ситуацию когда эти шарики стали липкими и тогда эти шарики будут еще сильнее сопротивлятся сдвигу. И вот чем сильнее они буду сопротивлятся сдвигу об друг друга, тем сильнее будет вязкость.

Название «кинематическая вязкость» не несет особого физического смысла, так как название было предложено потому, что размерность v похожа на размерность скорости.

Вязкость жидкости зависит как от температуры, так и от давления. Кинематическая вязкость капельных жидкостей уменьшается с увеличением температуры, а вот вязкость газов, наоборот, возрастает с увеличением температуры. Кинематическая вязкость жидкостей при давлениях, встречающихся в большинстве случаев на практике, мало зависит от давления, а вязкость газов с возрастанием давления уменьшается.

Вязкость жидкости измеряют с помощью вискозиметров различных конструкций.

3 Приборы для измерения давления

 

Для измерения давления или разрежения в технологических агрегатах, сосудах или трубопроводах отечественная промышленность выпускает две группы приборов:манометры, вакуумметры или мановакуумметры, а также напоромеры, тягомеры, тягонапоромеры. Первая группа применяется, когда измеряемой средой является жидкость или газ, вторая — только для газа, причем для более низких давлений, чем приборы первой группы. Верхние пределы шкал давления выбираются из ряда (1,0; 1,6; 2,5; 4,0; 6,0)-10™. Для измерителей разрежения (вакуумметров, мановаку-умметров) верхние пределы на единицу меньше (т. е. 0,6; 1,5; 3,0; 5,0)-10™, так как упомянутая единица (со знаком «минус») переходит в левую часть шкалы. Для второй группы приборов пределы шкал выбираются из тех же рядов. Выбирая шкалы приборов, необходимо давать запас по сравнению с максимальным рабочим давлением. Так, например, при измерении давления газов (включая воздух) запас принимают 20—25 %, а для холодной воды — 5—10 %. При измерении давлений агрессивных или загрязненных жидкостей и газов перед измерительным прибором ставится разделительное устройство. Между местом отбора давлений и прибором необходимо устанавливать трехходовые краны, позволяющие осуществлять поверку рабочего манометра без его демонтажа. Измерители давления подлежат обязательной государственной поверке в следующие сроки: манометры — 1 раз в год; остальные приборы этой группы — 1 раз в 2 года.

4Гидростатическая машина

Гидростатические машины являются обратимыми. Они могут работать как в режиме насоса, так и в режиме гидродвигателя. Например, если машина тормозится, то ее двигатели переходят на режим работы насоса, а насос - на режим работы двигателей. При этом магистрали высокого и низкого давления меняются местами: магистраль высокого давления А становится магистралью низкого давления, а магистраль низкого давления Б - магистралью высокого давления. Система подпитки в этом случае должна быть подключена к магистрали А. [1]

Всякая гидростатическая машина состоит из следующих основных частей: ротора, статора, уплотнителей и распределителей. [2]

Например, гидростатическая машина имеет два вида парных потоков: вращательные механические и поступательные гидравлические. Таким образом, механические потоки между собой однородны, а также однородны и гидравлические потоки. [5]

Рабочий цикл гидростатической машины состоит из двух процессов: наполнения рабочей камеры жидкостью и ее выталкивания из рабочей камеры в магистраль. [6]

Принцип действия гидростатических машин

Закон Паскаля имеет большое практическое применение и используется при создании различных гидравлических домкратов, гидравлических прессов, гидравлических приводов и других гидравлических систем, принцип действия которых основан на передаче давления внутри жидкости. Принцип действия таких устройств рассмотрим на примере определения грузоподъемности гидравлического домкрата (рис. 4.6).

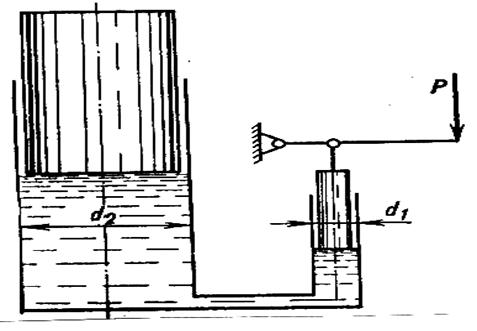
Рис 4.6. Гидравлический домкрат

Закон Архимеда

Закон Архимеда это основа основ гидравлики и всего что исходит из неё (гидродинамики, гидростатики, и всего что так или иначе связанно с водой) Закон Архимеда можно понять просто: на тело с массой погружённое в воду, действует выталкивающая сила равная массе погружённого тела. На примере это можно предствавить так:  1) Почему карабль вешающий большое количество тонн не тонет, потому что именно с тойже силой равная его массе выталкивет его на поверхность и получаюеться что силы А (архимеда) = mg (массе карабля)

­

2) Представь что ты как обычно залезаешь в ванну наполненой водой, ты наблюдаешь что уровень воды поднялся выше, из-за того что ты вытеснила своим телом воду, и эта вытесненная вода пытается встать снова на своё месно и таким образом выталкивает твоё тело, что и являеться действием Архимедовой силы которая заключена в Закон Архимеда (в ванне конечно ты не будешь плавать, так как в пронстранства там меньше, а вот в басеине пожалуста, там ты представляешь тем самым караблём) Архимедова сила может действовать не только в жидкости (вода), но также в газе и плазме

Формула в векторной форме

­

где  p — плотность жидкости (газа, плазмы), g — ускорение свободного падения,  V — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности).

ДВИЖЕНИЕ ЖИДКОСТИ

 

— основной вопрос, изучаемый гидромеханикой и гидравликой в разделе гидродинамика. Основные виды движения жидкости: равномерное и неравномерное; установившееся и неустановившееся; напорное и открытое (безнапорное); ламинарное и турбулентное. Установившееся неравномерное движение представляет практич. интерес только для открытых русел, т. к. трубопроводы обычно имеют постоянное по длине сечение, а относительно короткие переходные участки (конфузоры и диффузоры), характеризующиеся нек-рыми особенностями в отношении работы трения, учитываются как местные сопротивления в основном расчетном ур-нии Бернулли. Неравномерное движение в открытом русле может быть плавноизменяющимся или относительно резкоизменяющимся. В первом случае конвективная сила инерции играет небольшую роль и зачастую ею можно пренебрегать по сравнению с силой трения, во втором случае эти силы по меньшей мере соизмеримы. Значительное увеличение скорости на участке малой длины достигается в случае водосливов, перепадов, быстротоков (см. Гидравлика сооружений); такое же уменьшение скорости возможно в случае прыжка гидравлического. Неустановившееся равномерное движение практически возможно лишь в трубах постоянного сечения. Напр., в трубопроводе, питаемом поршневым насосом; в трубопроводе, подающем воду к турбине при колебаниях нагрузки ГЭС. Перед инерционным напором ставится знак плюс, если скорость в трубе с течением времени увеличивается, и минус, если скорость уменьшается. Потерянный напор hT при неустановившемся движении отличается от его значений в соответствующих условиях (при одинаковых шероховатости, вязкости, скорости, диаметре) установившегося движения, причем и при положительном и при отрицательном ускорении hT возрастает по сравнению с установившимся движением. При турбулентном движении это возрастание невелико, при ламинарном же может оказаться существенным. При очень большом локальном ускорении в трубах возникает особое явление, наз. гидравлическим ударом. Неустановившееся неравномерное движение представляет практич. интерес лишь для открытых русел, т. к. в трубах участки переменного сечения очень короткие и сила инерции массы жидкости, заполняющей эти участки, несущественна ио сравнению с силой инерции масс жидкости, заполняющих участки постоянного диаметра. Изменение скорости, а следовательно, и расхода с течением времени влечет за собой изменение глубины наполнения русла, причем оно происходит не синхронно ио всей длине потока, а начинается на одном из его концов и затем распространяется в виде волны, к-рая является волной изменения расхода и отличается от колебательных волн (ветровых, корабельных и др., см. Волны). Волны изменения расхода возникают в реках и каналах при наполнении и опорожнении камер судоходных шлюзов, при суточном колебании мощности гидроэлектростанций. Волна изменения расхода может быть: волной подпора, которая образуется при уменьшении расхода в конце рассматриваемого участка; волной излива — возникает при увеличении расхода в конце участка; волной попуска — образуется при увеличении расхода в начале рассматриваемого участка; волной отлива — создается при уменьшении расхода в начале участка.