398.Ортогональные системы функций. Изложенное в предыдущем номере является образцом рассуждений, которыми часто приходится пользоваться в математическом анализе при изучении многих разложений.

Назовём две функции и , определённые в промежутке [a, b], ортогональными в этом промежутке, если их произведение имеет интеграл, равный нулю:

Рассмотрим систему функций { }, определённых в промежутке [a, b] и непрерывных в нём или, по крайней мере, кусочно-непрерывных. Если функции данной системы попарно ортогональны:

(15)

(n, m=0, 1, 2, …; n m)

то её называют ортогональной системой функций. При этом мы всегда будем, предполагать, что

(16)

При соблюдении условий (n=0, 1, 2, …) система называется нормально. Если же эти условия не выполнены, то при желании можно перейти к системе , которая уже заведомо будет нормальной.

Важнейшим примером ортогональной системы функций как раз и является тригонометрическая система

1, cos x, sin x, cos 2x, sin 2x, …, cos nx, sin nx,… (17)

в промежутке , которую мы рассматривали выше; её ортогональность следует из соотношений (6), (8), (9) и (13). Однако нормальной она не будет ввиду (10) и (14). Умножая тригонометрические функции (17) на надлежащие множители, легко получить нормальную систему:

, …, , , … (17*)

Пусть в промежутке [a, b] дана какая-нибудь ортогональная система { }. Зададимся целью разложить определённую в [a, b] функцию f(x) в «ряд по функциям » вида

(18)

Для определения коэффициентов этого разложения, допуская его возможность, поступим так, как мы это сделали в частном случае выше. Именно, умножив обе части разложения на , проинтегрируем его почленно:

В силу ортогональности [см. (15) и (16)], все интегралы справа, кроме одного, будут нулями, и легко получается:

(m=0, 1, 2, …) (19)

[формулы (7), (11), (12) являются частными случаями этой формулы].

Ряд (18) с коэффициентами, составленными по формулам (19), называется (обобщенным) рядом Фурье данной функции, а сами коэффициенты – её (обобщёнными) коэффициентами Фурье относительно системы { }. Особенно просто выглядят формулы (19) в случае нормальной системы; тогда

. (19а)

Конечно, здесь могут быть повторены те же замечания, какими мы закончили предыдущий номер. Обобщённый ряд Фурье, построенный для данной функции f(x), связан с нею лишь формально. И в общем случае связь между функцией f(x) и её (обобщённым) рядом Фурье обозначают так:

~ (18а)

Сходимость этого ряда к функции f(x), как и в случае тригонометрического ряда, подлежит ещё исследованию.

§2.Разложение функций в ряд Фурье.

399. Постановка вопроса. Интеграл Дирихле. Пусть f(X) будет непрерывная или кусочно-непрерывная функция с периодом . Вычислим постоянные (её коэффициенты Фурье):

, (1)

(m=0, 1, 2,…) (m=1, 2 ,3, …)

и по ним составим ряд Фурье нашей функции

f(x)~ (2)

Читатель замечает здесь маленькое отступление от обозначений : коэффициент a₀ мы определяем теперь по общей формуле для a_m при m=0, в разрезе с формулой (7) упомянутого номера, но зато свободный член ряда пишем в виде .

Замечание. Если функция F(u) кусочно-непрерывная в любом конечном промежутке и к тому имеет период , так что

то величина интеграла

по промежутку длины не зависит от .

Действительно, ограничиваясь, случаем непрерывной функции F, имеем

Если в последнем интеграле сделать подстановку , то он приведётся к интегралу

и лишь знаком будет отличаться от первого интеграла. Таким образом, рассматриваемый интеграл оказывается равным интегралу

уже не содержащему . Легко распространить этот результат и на случай любой кусочно-непрерывной функции.

Этим замечанием мы в последующем будем пользоваться. В частности, и в формулах , определяющих коэффициенты Фурье, интегралы могут быть взяты по любому промежутку длины ; например, можно было бы писать

, (1а)

(m=0, 1, 2,…) (m=1, 2 , 3, …)

и т. п.

Для того, что бы исследовать поведение ряда (2) в какой-нибудь определённой точке , составим удобное выражение для его частичной суммы

Подставим вместо и их интегральные выражения (1) и подведём постоянные числа , под знак интеграла:

Легко проверить тождество

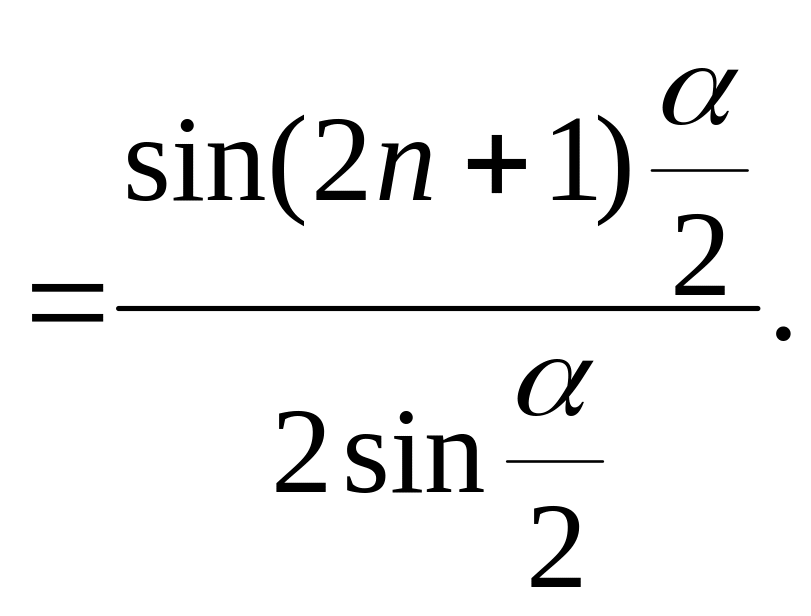
Воспользовавшись им для преобразования подынтегрального выражения, окончательно получим

(3)

Этот интеграл обыкновенно называют интегралом Дирихле (хотя у Фурье он встречается гораздо раньше !).

Так как мы имеем здесь дело с функциями от u периода , то промежуток интегрирования по сделанному выше замечанию можно заменить, например, промежутком [ ]:

Подстановкой преобразуем этот интеграл к виду

Затем, разбивая интеграл на два: , и приводя второй интеграл путём изменения знака переменной тоже к промежутку [ ], придём к такому окончательному выражению для частичной суммы ряда Фурье:

(4)

Таким образом, дело сводится к исследованию поведения именно этого интеграла содержащего параметры . Своеобразие представляющейся здесь задачи заключается в том, что в этом случае не может быть использован предельный переход под знаком интеграла ^*), который до сих пор [см. главу XVIII] служил нам единственным средством для разыскания интеграла, содержащего параметр. И с таким положением вещей нам в этой главе придётся сталкиваться систематически.