11. Запишите и поясните однородное дифференциальное уравнение свободных затухающих колебаний и его решение.

Общий вид однородного дифференциального уравнения свободных затухающих колебаний можно получить, обращаясь к формуле (14.16) для колебательного контура:

(15.6)

– однородное дифференциальное уравнение свободных затухающих колебаний, где под Q может подразумеваться любая физическая величина. В зависимости от физической природы колебательной системы коэффициент затухания и собственная частота (частота свободных незатухающих колебаний при отсутствии тормозящих сил в этой системе) описываются различными выражениями:

- для электрического колебательного контура сопротивлением R, электроемкостью C, индуктивностью L

, (15.7)

, (15.8)

;

11. Какие колебания называют вынужденными? Когда они возникают? Что называется резонансом? Где применяется это явление и где его пытаются устранить? Что происходит при резонансе в электрическом колебательном контуре? Переменная внешняя сила, приложенная к системе и вызывающая ее вынужденные колебания, называется возмущающей силой. Дифференциальное уравнение вынужденных колебаний величины S отличается от дифференциального уравнения свободных затухающих колебаний (15.6) только правой частью, не равной нулю. Правая часть содержит описание возмущающей силы F(t) и некоторый коэффициент a, определяемые физической природой колебательной системы:

.

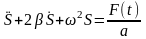Рассмотрим дифференциальное уравнение вынужденных колебаний простейшей линейной системы – пружинного маятника под действием переменной силы F(t):

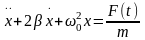. (15.14)

Сначала маятник участвует в двух колебаниях (так называемый переходный режим, рис. 15.2): x(t)=x₁(t)+x₂(t), где 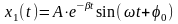– свободные (быстро) затухающие во времени колебания, обусловленные наличием сопротивления в среде 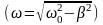, x(t)=x₂(t) – установившиеся колебания с частотой 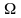действия переменной возмущающей силы F(t) – установившийся режим колебаний после переходного режима.

Рис. 15.2

Пусть вынужденные колебания происходят под действием возмущающей силы . Тогда установившиеся вынужденные колебания маятника будут совершаться по закону:

,

,

.

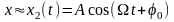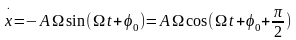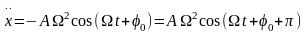С учетом данных выражений (15.14) примет вид:

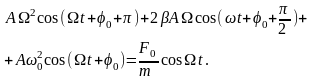
Так как сама величина х, ее первая и вторая производные, возмущающая сила F_x – есть величины переменные (колеблющиеся), то их все можно представить в виде вращающихся векторов с модулями соответственно , , , 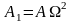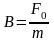(рис. 15.3):

.

При t=0 ( ) имеем:

,

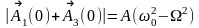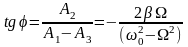. (15.15)

Рис. 15.3

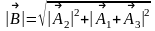
Из диаграммы 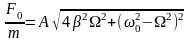, откуда амплитуда установившихся колебаний будет определяться выражением

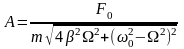. (15.16)

Для определения максимального значения А, исследуем знаменатель на экстремумы, находя производную по переменной (частоте) :

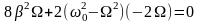, , отсюда 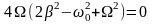; при 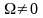равна нулю скобка и

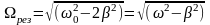, (15.17)

так как 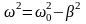. Здесь – циклическая частота свободных незатухающих (собственных), а – свободных затухающих колебаний колебательной системы. Формула (15.16) позволяет сделать интересный вывод: при приближении (совпадении) частоты возмущающей силы с резонансной частотой системы происходит резкое возрастание амплитуды вынужденных колебаний. Данное явление называется резонансом (рис. 15.4). Резонансная частота колебательной системы, определяется по формуле (15.16). 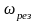Очевидно, чем меньше затухание, тем ближе резонансная частота к частоте собственных колебаний системы .

Рис. 15.4

В строительстве резонанса стараются избегать из-за опасности разрушения конструкций, а в радиотехнике стараются вызвать резонанс в колебательном контуре для усиления (выделения) улавливаемых антенной приемника колебаний. Рассмотрим подробнее последнее, полезное явление.