Вопросы к зачету гр.Аэс-10-д1, 5 семестр Общая физика

1. Что называется колебанием? Волной? Что называют слышимым звуком, инфразвуком, ультразвуком? Какие специфические свойства есть у каждого диапазона? Дайте определение периода колебаний, частоты и циклической частоты. В каких единицах их измеряют в системе СИ? Что называют фазой колебания? В чем она измеряется?

Колебаниями называются процессы, в той или иной степени повторяющиеся во времени. Так как подобные процессы протекают в системах разной физической природы, то различают механические, электромагнитные колебания, электромеханические и т.д. Периодичностью во времени и пространстве характеризуется волна. Область практического применения колебательных процессов – часы, радио, ТВ, акустика, связь (радио и теле). Зачастую колебательные процессы оказывают вредное воздействие на человеческий организм: например, шумы:

а) слышимые звуковые процессы (16<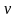 <20000 Гц), не несущие полезной информации, длительно воздействуя на организм, вызывают тугоухость, расстройство нервной системы (болезни);

б) инфразвук ( <16 Гц) при высокой интенсивности вызывает страх, панику; так как колебания воспринимаются всем телом (не слышим), то могут быть механические повреждения внутренних органов, а при длительном воздействии гибель; ультразвук ( >20000 Гц): вызывает головные боли, снижение тонуса организма;

в) вибрации (все перечисленные процессы, как правило, взаимосвязаны): при совпадении частот вибрации с частотами органов могут быть проблемы: если с частотой желудка – тошнота; может быть укачивание, головокружения; при длительном воздействии проявляется: при общей вибрации виброболезнь (головокружения, головные боли, снижение координации движений, может быть усиление отложения солей и развития остеохондроза); при локальной вибрации – потеря чувствительности, нарушение кровообращения (например, в руках);

г) ЭМВ воздействуют на все внутренние органы, могут быть даже ложные ощущения, например запах, при индуцировании электромагнитными полями (волнами) тока в нейронах, нарушаются обменные процессы.

Колебания называются периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся во времени, повторяются через равные промежутки времени.

Наименьший из них промежуток времени называется периодом Т. За это время система совершает одно полное колебание. Частотой периодического колебания называется величина =1/Т, равная числу полных колебаний в единицу времени.

Циклической (круговой) частотой называется величина 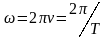, равная числу полных колебаний за 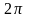секунд.

– фаза колебаний; 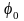– начальная фаза колебаний (в момент времени t=0); .

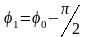2. Какие колебания называют гармоническими и свободными? Запишите дифференциальное уравнение свободных гармонических колебаний и его решение.

Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону.

 Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).

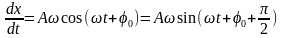. (14.3)

Т.е. первая производная по времени dx/dt опережает x по фазе на .

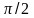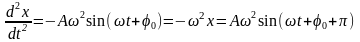. (14.4)

Т.е. вторая производная d²x/dt² опережает x по фазе на .

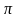Из (14.4) и (14.2^/) очевидно, что

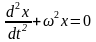(14.5)

– дифференциальное уравнение свободных незатухающих гармонических колебаний. Это линейное однородное дифференциальное уравнение второго порядка. Общее решение (14.5) можно записать в виде:

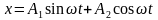. (14.6)

Константы 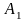и 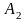определяют из начальных условий (при t=0):

; .

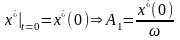Выражение (14.6) можно переписать в виде

, (14.7)

где , .

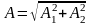Рис. 14.1

Гармонические колебания часто изображают графически вращающимися векторами (метод векторных диаграмм): проекция вектора 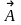на ось x совершает гармонические колебания (рис. 14.1).

Иногда вместо (14.2) удобно использовать комплексное выражение:

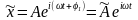, (14.8)

которое получается с использованием известной в математике формулы Эйлера:

.

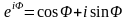3. Поясните на рисунке метод векторных диаграмм.

4. Как связаны между собой координата, скорость и ускорение колеблющегося тела?

5. Что называют математическим маятником? Пружинным? Крутильным? Физическим? Запишите и поясните формулы для периодов колебаний каждого из них.

Физический маятник – твердое тело, которое может совершать колебания под действием собственной силы тяж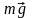ести вокруг неподвижной горизонтальной оси, не проходящей через центр масс тела и называемой осью качания. Центр тяжести маятника совпадает с его центром масс. Как правило, силой трения в подвесе маятника пренебрегают и момент относительно оси качания маятника создает только его сила тяжести .

Рассмотрим вариант физического маятника: материальную точку, закрепленную на жестком невесомом стержне длины d (рис. 14.5).

При отклонении маятника на угол момент, создаваемый силой тяжести равен 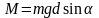. Согласно основному уравнению динамики вращательного движения (для тела с моментом инерции I, вращающегося вокруг неподвижной оси в отсутствие трения, (см. Часть I настоящего пособия, формула (4.24))) 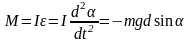(знак «–», так как момент силы тяжести возвращает систему в положение равновесия). При малых 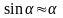(в радианах) .

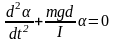Рис. 14.5

Сравнивая с уравнением свободных незатухающих гармонических колебаний (14.5): 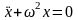, имеем для физического маятника

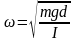, (14.14)

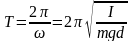. (14.15)

Данные формулы справедливы для физического маятника в общем случае.

в) Рассмотрим случай в) рис. 14.2 – математический маятник.

Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести, т.е. математический маятник представляет собой предельный случай физического маятника, когда вся масса сосредоточена в центре масс тела. При этом d=l – длина маятника и момент инерции 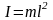, тогда формулы (14.14), (14.15) примут вид:

, .

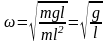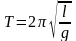Из данных формул видно, что частота и период колебаний не зависят от амплитуды (изохронные колебания) при малых колебаниях (малых ). В общем случае Т и 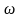зависят от амплитуды , но при увеличении до 15⁰ период Т изменяется до 0.5%. Длина математического маятника, имеющего такой же период колебаний, что и данный физический маятник, называется приведенной длиной 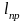этого физического маятника.

Согласно теореме Гюйгенса–Штейнера (см. Часть I настоящего пособия, формула (4.4)) момент инерции 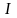тела относительно произвольной оси О₁ равен сумме моментов инерции тела относительно параллельной ей оси, проходящей через центр масс 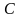тела, и произведения массы тела m на квадрат расстояния d между этими осями: 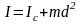. Тогда 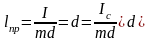, здесь – момент инерции физического маятника относительно оси, проходящей через центр масс 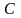маятника и параллельной его оси качания. Точка О₁, находящаяся на расстоянии от точки подвеса О маятника, называется центром качания физического маятника. Точки O и О₁ обладают свойством взаимности, т.е. при перемене их ролей длина и период маятника останутся прежними.

б) Рассмотрим случай б) рис. 14.2 – крутильный маятник.

Крутильный маятник – твердое тело, подвешенное на нити (проволоке) и способное совершать колебания под действием силы упругости закрученной нити (проволоки) вокруг вертикальной оси, обычно проходящей через центр масс тела.

Если твердое тело, обладающее моментом инерции I, подвешено на проволоке с коэффициентом упругости D, закрученной на малый угол , то согласно основному уравнению динамики вращательного движения (знак «–», так как момент силы упругости возвращает систему в положение равновесия). Отсюда 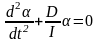, где

, .

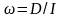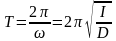6. Какую силу называют квазиупругой? Какую систему называют линейным гармоническим осциллятором? Как определить потенциальную, кинетическую и полную механическую энергию колеблющегося тела? Запишите и поясните формулы. КВАЗИУПРУГАЯ СИЛА

(от лат. quasi - как бы. наподобие) - перем. сила F, действующая на материальную точку М, пропорциональная и противоположная по направлению смещению г точки из положения равновесия О (см. рис.): F = - kr, где k - коэфф. К. с. Таковы, напр., упругие силы, возникающие при малых деформациях упругих тел (отсюда и название "К. с."), касательная составляющая силы тяжести, действующей на матем. маятник при малых его отклонениях. К. с. стремится возвратить материальную точку в положение равновесия и в отсутствие др. сил вызывает гармонические колебания материальной точки.

Система, совершающая колебания под действием квазиупругой силы (при условии (14.10^/) и (14.7)), называется линейным гармоническим осциллятором (ЛГО).

Исходя из вышесказанного с учетом (14.7), (14.3), (14.4) кинетическая энергия материальной точки

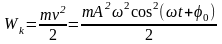, (14.11)

потенциальная энергия (рис. 14.3, случай а) рис. 14.2 – пружинный маятник)

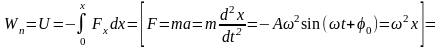
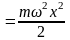, (14.12)

(при 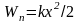), полная (механическая) энергия

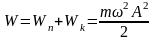. (14.13)

Рис. 14.3

Рис. 14.4

На рис. 14.3 видно, что классическая колеблющаяся точка не может выйти за границы отрезка 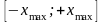, т.е. находится в потенциальной яме параболической формы.

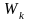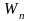Из (14.11)–(14.13) видно, что колебания и совершаются со сдвигом по фазе на и, следовательно, полная механическая энергия материальной точки при свободных незатухающих гармонических колебаниях не изменяется со временем