Московский государственный технический университет им. Н.Э. Баумана

Домашнее задание

Распад произвольного разрыва

Выполнил: Кобзев А.С.

Группа: СМ3-93

Преподаватель: Голубев А.Г.

Москва

2012

Исходные данные

1.Параметры газа в области 1 и 2:

k₁, k_2;

R₁, R₂;

2.Скорости движения сред в области 1 и 2:

u₁, u_2;

3.Давление в области 1 и 2:

p₁, p_2;

4.Температура в области 1 и 2:

Т₁, Т_2.

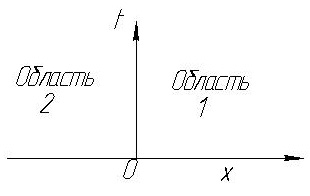
Найти:

1. Структуру, возникающую при распаде;

2. Определить параметры в общей области;

3. Определить параметры на разрывах (на ударных волнах и волнах разряжения);

4. Определить изменение параметров внутри волны разряжения если есть в структуре;

5. Представить параметры в двух координатных системах х(t) и Р, М,ρ, Т(х/t).

Теоретическая часть

Задача о распаде произвольного разрыва — задача о построении аналитического решения нестационарных уравнений механики сплошных сред, в применении к распаду произвольного разрыва.

Вычисление параметров потока при распаде произвольного разрыва представляет собой автомодельную задачу для одномерного течения газа. Ее решение может быть использовано как для анализа различных нестационарных течений газа, так и в качестве элемента численного метода расчета. Однако независимо от того, в какой области исследования применяется эта задача, общая структура ее решения имеет законченный вид и может быть рассмотрена отдельно.

Постановка задачи: полагается, что до начального момента времени t = 0 две области пространства с различными значениями термодинамических параметров (плотность, скорость и давление газа) были разделены тонкой перегородкой, а в начальный момент времени перегородку убирают. Требуется построить решение (то есть зависимость всех термодинамических параметров от времени и координаты) при произвольных начальных значениях переменных.

При внезапном удалении перегородки между двумя массами газа образуется поверхность контактного разрыва (КР). В следующий момент времени разрыв распадется на устойчивые схемы течения, которые могут существовать в газе: ударные волны (УВ) или волны разряжения (ВР), причем в каждую сторону начнет двигаться только одна из волн.

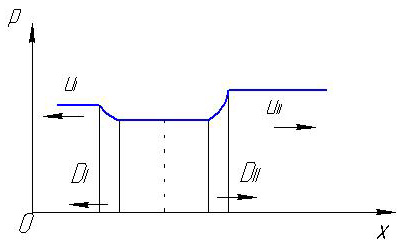
а)Характер изменения давления при движении двух потоков один навстречу другому со скоростями u_I и u_II. В этом случае возникают две разбегающиеся УВ, скорости которых соответственно равны D_I и D_II.

б) При первоначальном соприкосновении двух неподвижных или движущихся в одну сторону с одинаковыми скоростями масс газа, сжатых до различных давлений, в одну сторону будет распространяться ударная волна, а в другую - волна разряжения.

в) В обе стороны распространяются волны разрежения. Такой вариант возникает, если в начальный момент времени соприкасающиеся массы газа имеют скорости, направленные в разные стороны от поверхности контактного разрыва.

Позади каждой из движущихся волн, т.е. вблизи начала координат, статическое давление газа выравнивается и его скорость одинаковая. Однако плотность и внутренняя энергия при этом могут изменятся. Такое скачкообразное изменение параметров называется контактным разрывом.

Поскольку скорости движения волн D_I и D_II постоянны, на плоскости Охt автомодельную картину возникающего течения можно изобразить одной из возможных схем, представленных на рисунке.

Поверхность КР размещена в пространстве между двумя волнами и движется в направлении одной из них с меньшей скоростью, поэтому на плоскости Охt она разбивает область между волнами на две подобласти (слева и справа от разрыва). Эти подобласти отделены от невозмущенных областей либо УВ, либо ВР.

Автомодельная система обыкновенных дифференциальных уравнений для одномерного нестационарного движения газа:

Краевые условия на бесконечности:

при ζ=+∞ u=u₁, ρ= ρ₁, p=p₁;

при ζ= -∞ u=u₂, ρ= ρ₂, p=p₂.

Решение задачи строится:

• из областей с постоянными параметрами, разделенными линиями разрыва(УВ и КР);

• и из областей с непрерывно меняющимися параметрами (из центрированных волн разряжения).

Алгоритм анализа структуры распада базируется на уравнении:

где Ψ – это функция скорости:

1. Введем вспомогательную функцию χ:

2. Определяем вид волн.

Обозначим за p_max – наибольшее давление из p₁ и p₂,

а за p_min – наименьшее давление из p₁ и p₂.

Тогда:

• Если имеем решения нет (газы разлетаются таким образом, что между ними образуется вакуум);

• Если имеем в обеих областях имеет место волна разряжения;

• Если имеем в область 2 идет ударная волна в область 1 – в сторону большего давления – волна разряжения;

• Если имеем в обе области уходят ударные волны.

3. Решая уравнение (1) методом касательных находим p_o, по которому можем найти все параметры в общей области:

4. Определяем скорость перемещения ударной волны (из соотношений Гюгонио):

5. Определяем скорость перемещения фронтов волны разряжения:

Скорость перемещения заднего фронта

Скорость перемещения переднего фронта

Задание: