27. Зовнішня задача Діріхле.

(ДРЧП) , ,

(ГУ) , ,

розв’язується так само, як і внутрішня задача, за винятком того, що тепер потрібно відкинути ті розв'язки, які не є обмежені при прямуванні до нескінченності, тобто , , .

Тому в якості розв'язку залишається взяти функцію

,

де коефіцієнти , обчислюються за тими ж формулами, що й раніше: ,

, .

Іншими словами, ми просто розкладаємо функцію в ряд Фур’є

,

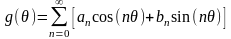а потім кожен член цього ряду домножаємо на коефіцієнт .

На закінчення відзначимо, що ми обмежилися розглядом лише двовимірних однорідних задач. Не менший інтерес викликають й еліптичні задачі з неоднорідними ДРЧП та ГУ, а також задачі в просторах вищої розмірності.

26. Рівняння Лапласа в крузі

Постановка задачі. Знайти таку функцію , що задовольняє системі

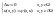
Виконаємо перехід до полярної системи координат

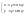
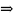
з того, що ,

Виконуючи елементарні перетворення, тобто знаходячи частинні похідні та , потім та , виконавши підстановку в рівняння Лапласа знайдених похідних отримаємо

Отримати рівняння Лапласа в полярній системі координат.

Задачу будемо розв’язути методом Фур’є

Шукаємо функцію 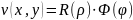, виконуючи підстановку отримаємо

Загальний розв’язок:

24.Функція Гріна

Метод функції Гріна зручно застосовувати для еліптичних рівнянь. Цей метод дає змогу записати розв’язок задачі у вигляді інтегралів.

Розглянемо задачу

Де - двовимірна або 3-вимірна область з межею ; 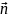- зовнішня нормаль до . При маємо першу крайову задачу або задачу Діріхле, при - другу крайову задачу або задачу Неймана, а при - третю крайову задачу. Функцією Гріна задачі(1) наз. функція яка задовольняє такі умови:

1. - гармонічна як функція в 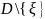і при перетворюється у нескінченність;

2. задовольняє крайову умову ;

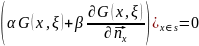3. в області функція допускає зображення: а) для б) для де - відстань між точками і , а - гармонічна функція в . Ф-я (1) симетрична, тобто При відповідній гладкості поверхні та функцій і розв'язок 1-ї, 2-ї і 3-ї крайових задач для 3-вимірного випадку записується відповідно у вигляді

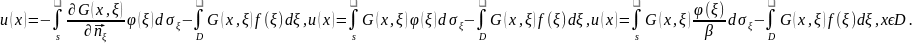
19. Побудова розв’язку першої краєвої задачі для рівняння теплопровідності методом Фур’є.

1. Побудова розв’язку першої краєвої задачі рівняння теплопровідності методом Фур’є.

Постановка задачі.

Знайти функцію , що задовольняє рівняння та умовам першої краєвої задачі

Розділимо змінні.

- добуток двох функцій

,

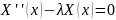
Розв’язком задачі при

;

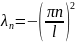
Загальний розв’язок

;

;

,

;

;

; ;
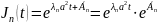
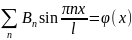