
- •1.Класифікація і зведення до кан вигляду рівн з похід.: рівняння гіперболічного типу
- •3.Класифікація і зведен до кан вигляду рівн з похід.: рівняння параболічного типу типу
- •7. Краєві та початкові умови для рівняння коливання струни.
- •10. Розвязування задачі для напівскінченної струни за допомогою формули д’Аламбера
- •15. Крайові та початкові умови для рівнянь теплопровідності
- •11 Побудова розв’язку першої краєвої задачі для хвильового рівняння
- •8. 9. Формула д’Аламбера. Розвязування задачі Коші для хвильового рівняння методом д’Аламбера
- •5,6. Рівняння поперечних коливань струни.
- •2.Класифікація і зведен до кан вигляду рівн з похід.: рівняння еліптичного типу
- •17. Єдиність розв'язку краєвої задачі для рівняння коливання струни
- •27. Зовнішня задача Діріхле.
- •26. Рівняння Лапласа в крузі
- •24.Функція Гріна
- •19. Побудова розв’язку першої краєвої задачі для рівняння теплопровідності методом Фур’є.
5,6. Рівняння поперечних коливань струни.
Струна –це пружна нитка, котру можна згинати, але її не можна розтягувати.
Нехай
маємо струну довжина якої
 .
Спрямуємо вісь ОХ вздовж струни, що
знаходиться в положенні рівноваги.
Нехай
.
Спрямуємо вісь ОХ вздовж струни, що
знаходиться в положенні рівноваги.
Нехай
 =0
–лівий
кінець струни,
=0
–лівий
кінець струни,
 –правий
кінець струни. І будемо розглядати лише
поперечні коливання струни, т.т. рух
точок буде проходити перпендикулярно
до вісі ОХ
–правий
кінець струни. І будемо розглядати лише
поперечні коливання струни, т.т. рух
точок буде проходити перпендикулярно
до вісі ОХ
в площині
 ,
котра буде описувати зміщення точок
струни від положення рівноваги в момент
часу
,
котра буде описувати зміщення точок
струни від положення рівноваги в момент
часу
 .
.
Будемо
припускати, що
 є
є
 ,
а відхилення точок струни від положення
рівноваги досить малі порівняння з її
довжиною.
,
а відхилення точок струни від положення
рівноваги досить малі порівняння з її
довжиною.
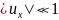
Приріст
функції
 має вигляд
має вигляд
 .
.
Довжина
ділянки струни






Отже в
такому разі
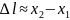 .
Із вище сказаного слідує, що точки
струни коливаються перпендикулярно
до вісі ОХ, але при цьому відстані між
ними не змінюються.
.
Із вище сказаного слідує, що точки
струни коливаються перпендикулярно
до вісі ОХ, але при цьому відстані між
ними не змінюються.
Закон Гука: була довжина L, застосували силу T, довжина стала L'
T=T(L')
Закон
Гука має вигляд T=ES
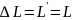
S –поперечний переріз площини
E –модуль Юнга.
Так як за припущенням до до струни відстань між точками не змінюється, то натяг струни не буде залежати від часу T=T(х).
Натягом
називається сила, з якою правий кінець
струни діє на лівий. Нехай
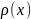 лінійна густина струни. Маса кусочка
струни між точками
лінійна густина струни. Маса кусочка
струни між точками
 визначається
визначається
 .
.
 –рівняння коливання
струни.
–рівняння коливання
струни.
Якщо
струна однорідна то




2.Класифікація і зведен до кан вигляду рівн з похід.: рівняння еліптичного типу
Диференціальне рівняння другого порядку в частинних похідних має вигляд:
A,B,C,D,F – певні функції, які залежать від . Якщо A,B,C,D,F – сталі, то рівняння назив. лінійним рівнянням за сталими коефіцієнтами.
Якщо то рівняння є однорідним, в іншому випадку неоднорідним. Щоб звести дане рівняння до канонічної форми застосовують заміну незалежних змінних
Рівнянь з частинними похідними класифікуються відносно значення виразу
Якщо - то рівняння гіперболічного типу. рівняння параболічного типу. рівняння еліптичного типу.
Розглянемо зведення до канонічного рівняння диф. рівняння еліптичного типу.
Складаємо рівняння характеристик:
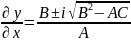
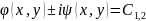

Для того щоб існували обернені перетворення необхідно і достатньо, щоб якобіан .
відповідно до замін, рівняння матиме вигляд
Шукаємо похідні з новими замінами:
Якщо підставити знайдені похідні у початкове рівняння та звести подібні, то рівняння матиме вигляд:
Для еліптичного виду рівняння канонічний вигляд такий:

17. Єдиність розв'язку краєвої задачі для рівняння коливання струни
Нехай
функції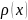 і
і
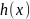 в рівнянні коливання струни:
в рівнянні коливання струни:


Тоді не може існувати двох розв’язків, що задовольняють рівняння коливання струни.
Розглянемо
першу задачу коливання струни.Доводити
будемо методом від супротивного. Нехай
в деякій області
 існує два розв’язки:
існує два розв’язки:
 .
.
Для
функції

 ;
;

 ;
;

Виконуючи віднімання першого рівняння від другого, отримаємо:
 .
.
Аналогічно віднімаючи відповідні умови будемо мати:
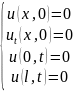
Розв’язуючи
отриману
задачу,
покажемо,
що
її
розв’язком
є
тільки
функція
 .
Для доведення
цього твердження розглядається одаткова
функція
.
Для доведення
цього твердження розглядається одаткова
функція
 ,
що представлена у вигляді інтегралу
,
що представлена у вигляді інтегралу
 ,
,

Знайдемо
похідну по
від обох частин рівності:
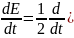

Покажемо, що отриманий інтеграл рівний нулю. Для цього виконаємо елементарні перетворення:
Розкриємо дужки:
 .
У рівнянні це означає, що
.
У рівнянні це означає, що

 ,
,
 .
Отже
.
Отже
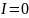 .
А
,
тоді, коли підінтегральна функція
дорівнює нулю.
.
А
,
тоді, коли підінтегральна функція
дорівнює нулю.
Так,
як підінтегральна функція
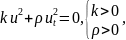 то
то ,
,
 і
і
 .
.
22-23. Поняття про задачу Штурма-Ліувілля. Задача Штурма-Ліувілля.
Задача
Штурма Ліувілля
полягає
у відшукуванні нетривіальних (тобто
відмінних відтотожного нуля) розвязку
на проміжку
Ліувілля
полягає
у відшукуванні нетривіальних (тобто
відмінних відтотожного нуля) розвязку
на проміжку однорідного рівняння
однорідного рівняння ,
що задовольняють однорідним граничним
умовам:
,
що задовольняють однорідним граничним
умовам:

і
значень параметра ,
при яких такі розв’язки,
що задовольняють вказаним граничним
умовам, існують.
,
при яких такі розв’язки,
що задовольняють вказаним граничним
умовам, існують.
Оператор це
лінійний диференціальний оператор
другого порядку, що діє на функцію
це
лінійний диференціальний оператор
другого порядку, що діє на функцію ,
виду
,
виду
 (оператор
Штурма
Ліувіля),
(оператор
Штурма
Ліувіля),
 аргумент.
аргумент.
Функції передбачаються неперервними
на
передбачаються неперервними
на ,
крім того функції
,
крім того функції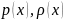 додатні
на
.
додатні
на
.
Шукані нетривіальні розв’язки називаються власними функціями цієї задачі, а значення , при яких такий розвязок існує, її власними значеннями (кожному власному значенню відповідає власнафункція).
Задача Штурма Ліувілля:

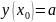

 ;
;

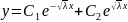
 ;
;

 тривіальні
розв’язки системи, то
тривіальні
розв’язки системи, то

Визначник головної матриці системи повинен дорівнювати 0, для того щоб знайти ще один розв’язок відмінний від тривіального.




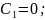

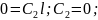


 .
.
Якщо
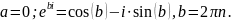
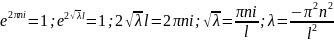

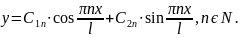

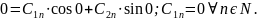



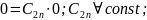
 загальний
розвязок
загальний
розвязок
Використовуючи властивості лінійного оператора
 розв’язок
задачі Штурма
Ліувілля
розв’язок
задачі Штурма
Ліувілля
25. Інтегральна формула Пуассона.
Візьмемо розв'язок задачі Діріхле, отриманий методом відокремлення змінних,
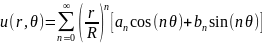
(ми беремо випадок довільного радіуса круга) і підставимо в нього формули для обчислення коефіцієнтів і . Після ряду обрахунків з використанням алгебри, інтегрального числення й тригонометрії отримуємо

Останній вираз у правій частині називається інтегральною формулою Пуассона. Отже, ми отримали ще одну форму зображення розв'язку внутрішньої задачі Діріхле
 (1)
(1)
Проаналізуємо розв'язок (1).
Можна вважати, що за формулою Пуассона (1) потенціал в точці
 є зваженим середнім граничного
потенціала. Вагова функція називається
ядром Пуассона
і має вигляд
є зваженим середнім граничного
потенціала. Вагова функція називається
ядром Пуассона
і має вигляд
Ядро Пуассона =
 .
.
Це дозволяє нам дещо сказати про фізику системи, а саме: потенціал в точці є зваженим середнім потенціалів сусідніх точок. Ядро Пуассона показує лише, який внесок кожної точки в загальний потенціал.
Розв'язок

зважена сума граничних потенціалів;
зважена сума граничних потенціалів;
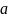
квадрат цієї довжини є знаменником
ядра Пуассона.
квадрат цієї довжини є знаменником
ядра Пуассона.
Для граничних
значень
 ,
близьких до
,
ядро Пуассона стає великим, оскільки
знаменник ядра дорівнює квадрату
відстані між точками
,
близьких до
,
ядро Пуассона стає великим, оскільки
знаменник ядра дорівнює квадрату
відстані між точками
 і
,
а, отже, є малим. Завдяки цьому більший
внесок в інтеграл дають значення
і
,
а, отже, є малим. Завдяки цьому більший
внесок в інтеграл дають значення
 ,
для яких
близькі до
.
На жаль, коли точка
як завгодно близько підходить до межі
,
для яких
близькі до
.
На жаль, коли точка
як завгодно близько підходить до межі
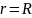 ,
то ядро Пуассона теж необмежено зростає.
Тому числові значення розв'язку біля
межі зручніше обчислювати за допомогою
рядів.
,
то ядро Пуассона теж необмежено зростає.
Тому числові значення розв'язку біля
межі зручніше обчислювати за допомогою
рядів.
Якщо обчислити потенціал в центрі круга за формулою Пуассона, то отримаємо
 .
.
Іншими словами, потенціал в центрі круга дорівнює середньому значенню потенціала на полі.


