15. Крайові та початкові умови для рівнянь теплопровідності

Крайові умови:

1. –крайові умови Діріхле (умови першого роду).

2. – умови Неймана (умови другого роду)

Для рівняння теплопровідності умови за номером 1) та 2) визначаються аналогічно. Крайові умови третього роду можна записати також за аналогією, але в коефіцієнти вкладається зовсім інший фізичний зміст.

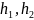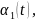При розв’язуванні задач струни та теплопровідності всі функції коефіцієнти та функції та є наперед заданими

Задача

“ Визначити функції для рівняння коливання струни

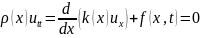і умови першого роду: ,

.”

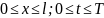11 Побудова розв’язку першої краєвої задачі для хвильового рівняння

Основне одномірне рівняння теплопровідності записується у вигляді .

Це рівняння зв’язує між собою величину – швидкість зміни температури за часом (вимірюється в град/с)та величину – вгнутість температурного профілю u(t,x).

Це рівняння ми отримаємо пізніше з основного рівняння збереження кількості тепла. Зараз ми вважаємо його заданим. Це рівняння говорить про те, що температура u(t,x) збільшується ( ) або зменшується (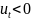 ) у відповідності з тим, додатна чи від’ємна друга похідна .

Подивимося, як можна інтерпретувати величину на мові теплопровідності. Припустимо, що ми апроксимуємо величну кінцевими різницями:

Це співвідношення можна переписати у вигляді

Тепер можна дати таку інтерпретацію величині :

1. Якщо температура u(t,x) менша за середнє значення температури в двох сусідніх точках, то

2. Якщо u(t,x) дорівнює середньому значенню температури в двох сусідніх точках, то

3. Якщо u(t,x) більша за середнє значення температури в двох сусідніх точках, то

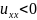
Коефіцієнт пропорційності 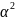визначається властивостями матеріалу.

8. 9. Формула д’Аламбера. Розвязування задачі Коші для хвильового рівняння методом д’Аламбера

Розглянемо задачу Коші для одновимірного хвильового рівняння

(ДРЧП) , -∞<x<∞, 0<t<∞

(ПУ) -∞<x<∞ (1)

Розв’язування задачі (1) розіб’ємо на кілька кроків.

Крок 1. Заміна координат t, x новими канонічними координатами 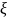, : , які зводять рівняння (1) в рівняння .

Крок 2. Розв’язування перетвореного рівняння: , довільна функція змінної , .

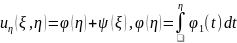Отже, загальний розв’язок рівняння записується у вигляді (2)

Крок 3. Повернення до початкових координат t, x. Для знаходження загального розв’язку рівняння (1) підставимо в розв’язок (2). В результаті отримаємо (3)

Це загальний розв’язок рівняння (1). З фізичної точки зору він цікавий тим, що є сумою двох біжучих хвиль довільної форми, які рухаються в протилежних напрямках зі швидкістю c.

Наприклад, –хвиля, яка рухається зліва направо. 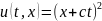– хвиля рухається справа наліво.

Крок 4. Врахування початкових умов.

Нагадаємо загальний метод розв’язування задачі Коші в теорії ЗДР. Спочатку знаходять загальний розв’язок рівняння, а потім він підставляється в початкові умови для того, щоб знайти конкретні значення довільних сталих.

Для розв’язування задачі Коші (1) підставимо загальний розв’язок (3) хвильового рівняння (який містить дві довільні функції) в початкові умови, щоб знайти конкретні вирази для функцій і . Маємо:

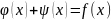
(4)

Проінтегрувавши другу рівність в межах від до x, отримаємо (5)

Тоді із (4) і (5) отримуємо ,

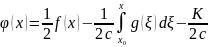а тому ,

,

отже, (6)

Ми отримали загальний розв’язок задачі (1). Розв’язок вигляду (6) за традицією називають формулою д’Аламбера.

x