
- •1.Класифікація і зведення до кан вигляду рівн з похід.: рівняння гіперболічного типу
- •3.Класифікація і зведен до кан вигляду рівн з похід.: рівняння параболічного типу типу
- •7. Краєві та початкові умови для рівняння коливання струни.
- •10. Розвязування задачі для напівскінченної струни за допомогою формули д’Аламбера
- •15. Крайові та початкові умови для рівнянь теплопровідності
- •11 Побудова розв’язку першої краєвої задачі для хвильового рівняння
- •8. 9. Формула д’Аламбера. Розвязування задачі Коші для хвильового рівняння методом д’Аламбера
- •5,6. Рівняння поперечних коливань струни.
- •2.Класифікація і зведен до кан вигляду рівн з похід.: рівняння еліптичного типу
- •17. Єдиність розв'язку краєвої задачі для рівняння коливання струни
- •27. Зовнішня задача Діріхле.
- •26. Рівняння Лапласа в крузі
- •24.Функція Гріна
- •19. Побудова розв’язку першої краєвої задачі для рівняння теплопровідності методом Фур’є.
1.Класифікація і зведення до кан вигляду рівн з похід.: рівняння гіперболічного типу
Диференціальне рівняння другого порядку в частинних похідних має вигляд:
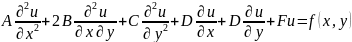
A,B,C,D,F –
певні функції, які залежать від
 .
Якщо A,B,C,D,F
– сталі, то рівняння назив. лінійним
рівнянням за сталими коефіцієнтами.
.
Якщо A,B,C,D,F
– сталі, то рівняння назив. лінійним
рівнянням за сталими коефіцієнтами.
Якщо
 то рівняння є однорідним, в іншому
випадку неоднорідним. Щоб звести дане
рівняння до канонічної форми застосовують
заміну незалежних змінних
то рівняння є однорідним, в іншому
випадку неоднорідним. Щоб звести дане
рівняння до канонічної форми застосовують
заміну незалежних змінних

Рівнянь
з частинними похідними класифікуються
відносно значення виразу

Якщо
 - то рівняння гіперболічного типу.
- то рівняння гіперболічного типу.
 рівняння параболічного типу.
рівняння параболічного типу.
 рівняння еліптичного типу.
рівняння еліптичного типу.
Розглянемо зведення до канонічного рівняння диф. рівняння гіперболічного типу.
Складаємо рівняння характеристик:



Для того
щоб існували обернені перетворення
 необхідно і достатньо,
щоб якобіан
необхідно і достатньо,
щоб якобіан
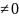 .
.
 відповідно до
замін,
рівняння матиме вигляд
відповідно до
замін,
рівняння матиме вигляд

Шукаємо
похідні з новими замінами:





Якщо підставити знайдені похідні у початкове рівняння та звести подібні, то рівняння матиме вигляд:




Для еліптичного виду рівняння канонічний вигляд такий:
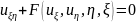
3.Класифікація і зведен до кан вигляду рівн з похід.: рівняння параболічного типу типу
Диференціальне рівняння другого порядку в частинних похідних має вигляд:
A,B,C,D,F – певні функції, які залежать від . Якщо A,B,C,D,F – сталі, то рівняння назив. Лінійним рівнянням за сталими коефіцієнтами.
Якщо то рівняння є однорідним, в іншому випадку неоднорідним. Щоб звести дане рівняння до канонічної форми застосовують заміну незалежних змінних
Рівнянь з частинними похідними класифікуються відносно значення виразу
Якщо - то рівняння гіперболічного типу. рівняння параболічного типу. рівняння еліптичного типу.
Розглянемо зведення до канонічного рівняння диф. рівняння параболічного типу.
Складаємо рівняння характеристик:



Для того щоб існували обернені перетворення необхідно і достатньо, щоб якобіан .
відповідно до замін, рівняння матиме вигляд
Шукаємо похідні з новими замінами:
Якщо підставити знайдені похідні у початкове рівняння та звести подібні, то рівняння матиме вигляд:
Для еліптичного виду рівняння канонічний вигляд такий:

7. Краєві та початкові умови для рівняння коливання струни.
Виведемо з другого закону Ньютона краєві та початкові умови. Як відомо початок координати і швидкість центру мас визначається за формулою




 –деякі
наперед задані функції. Це і є початковими
умовами коливання струни.
–деякі
наперед задані функції. Це і є початковими
умовами коливання струни.
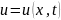
 –краєві
умови Діріхле
–краєві
умови Діріхле –умови
другого роду Неймана
–умови
другого роду Неймана –умови
третього роду (на основі закону Гука)
–умови
третього роду (на основі закону Гука)
10. Розвязування задачі для напівскінченної струни за допомогою формули д’Аламбера
Поставимо перед собою задачу: знайти хвильові рухи напівнескінченної струни, лівий кінець якої жорстко закріплено при даних початкових умовах. Тут є додаткова гранична умова (ГУ), а тому задача має такий вигляд:
(ДРЧП)
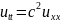 ,
-∞<x<∞,
0<t<∞
,
-∞<x<∞,
0<t<∞
(ГУ)
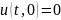 0<t<∞ 0<t<∞
0<t<∞ 0<t<∞
(ПУ) -∞<x<∞,
(1)
-∞<x<∞,
(1)
Підставивши
загальний розв’язок
 в початкові умови, маємо
в початкові умови, маємо
 (2)
(2)
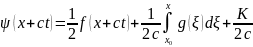
Тепер
виникає проблема, якої не було під час
розв’язування задачі Коші. Розв’язок
 повинен бути визначеним скрізь лише
всередині першого квадранта
повинен бути визначеним скрізь лише
всередині першого квадранта
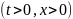 площини змінних
площини змінних
 .
Отже, ми повинні вміти обчислити значення
функції
.
Отже, ми повинні вміти обчислити значення
функції
 для всіх -∞<x-ct<∞
а значення функції
для всіх -∞<x-ct<∞
а значення функції
 для всіх -∞<x+ct<∞.
для всіх -∞<x+ct<∞.
На жаль,
перша з формул (2)
дозволяє
обчислювати
лише для
 ,
оскільки в початкових умовах функції
f(x)
та
g(x)
визначені лише для додатних значень
аргумента.
,
оскільки в початкових умовах функції
f(x)
та
g(x)
визначені лише для додатних значень
аргумента.
Якщо
,
то

Що
робити, коли x<ct?
Для цього скористаємося граничною
умовою
.
З її допомогою доозначимо функцію
для x<ct.
Підставивши
 в граничну умову отримаємо
в граничну умову отримаємо
 ,
звідки
,
звідки
 .
.
Підстановка
знайденого значення
 в загальний розв’язок дає
в загальний розв’язок дає
 0<x<ct,
0<x<ct,
Комбінуючи
розв’язки для x<ct
та x>ct,
нарешті отримуємо
 розв'язок задачі (1).
розв'язок задачі (1).
12-13-14. Рівняння теплопровідності.
(ДРЧП)
 ,
0< x
<L,
0< t
<∞;
,
0< x
<L,
0< t
<∞;
(ГУ)
 0< t
<∞;
(1)
0< t
<∞;
(1)
(ПУ)
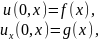 0≤
x
≤L.
0≤
x
≤L.
Щоб розв’язати задачу (1), знайдемо спочатку стоячі хвилі, тобто розв'язки вигляду
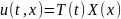 (2)
(2)
Підставивши (2) в (1) і відокремивши змінні, отримуємо два звичайних диференціальних рівняння
 (3)
(3)
Нашим
умовам задовольнятимуть лише розв'язки,
які відповідають


Послідовність елементарних коливань струни має вигляд

де an , bn – довільні дійсні сталі.

Отже, задача розв’язана. Її розв'язок має вигляд

Де
 ,
,
 знаходиться за формулами (6).
знаходиться за формулами (6).
