
- •12 Кинетическая энергия мат точки, система мат точек вращающегося тела. Закон изменения кинетической энергии. Работа силы. Мощность.
- •13.Работа силы при вращении.
- •14.Потенциальная энергия в поле силы.
- •15 .Потенциальная энергия тела в поле тяжести на малых высотах.
- •21Объекты и задачи термодинамики. Модель макросистемы – идеальный газ. Параметры состояния p V. Температура. Уравнение состояния идеального газа. Внутренняя энергия идеального газа.
- •22Работа, совершаемая газом в различных процессах.
- •23 Теплота. Первый закон термодинамики. Теплоемкость. Теплоемкость идеального газа в различных процессах.
- •24 Преобразование теплоты в работу. Вечный двигатель второго рода. Второй закон термодинамики. Тепловые машины.
12 Кинетическая энергия мат точки, система мат точек вращающегося тела. Закон изменения кинетической энергии. Работа силы. Мощность.
U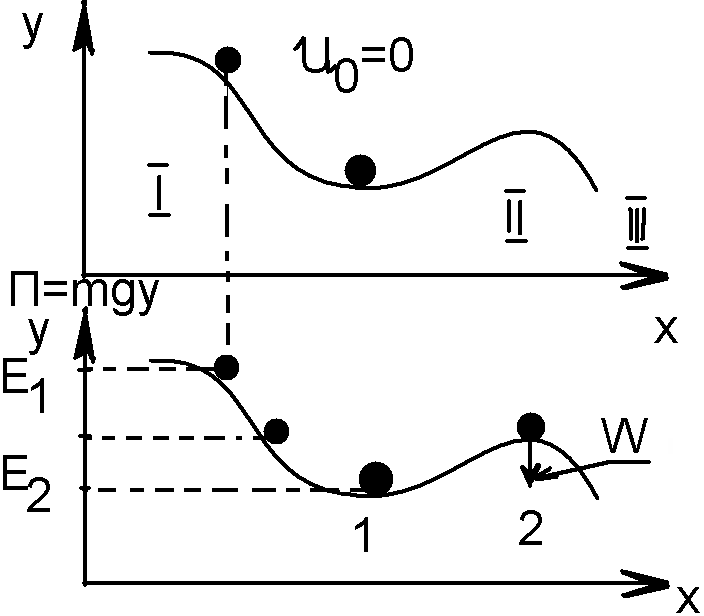
![]()
![]()
![]()
![]() 2→=?.
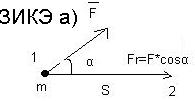
Решение: Разобьём наши действие на
элементарные участки dr→
α=(F→,dr→)
Fr=F*cos
α Fr-проекция
силы на элементарное перемещение
dr→.Dp→/dt=F→
→ m*dU→/dt=F→
| *U→mU→*dU→/dt=F→*U→
(A)
d/dt(mU2/2)=m/2*2U→*
dU→/dt=
mU→*dU→/dt
(A)→
mU→*dU→/
2→=?.
Решение: Разобьём наши действие на
элементарные участки dr→
α=(F→,dr→)
Fr=F*cos
α Fr-проекция
силы на элементарное перемещение
dr→.Dp→/dt=F→
→ m*dU→/dt=F→
| *U→mU→*dU→/dt=F→*U→
(A)
d/dt(mU2/2)=m/2*2U→*
dU→/dt=
mU→*dU→/dt
(A)→
mU→*dU→/dt
= F→*dr→/dt
d(
mU2/2
)=F→*dr→
(B)
U→*
U→=U*U=U2
T=
mU2/2
(1).Кинетическая
энергия. dA=F→*dr→=F*dr*cos
α (2) dT=dA (3) | 2∑1
Элементарное
изменение энергии материальной точки
равно элементарной работе всех сил.2∑1
dT=2∑1
dA
∆T=T2-T1=A1,2
∆T=A1,2
(4) Закон
изменения кинетической энергии. Изменение
Wn(частицы)
и на систему частиц равно работе всех
действующих над ней. A1,2=2∑1
dA=2∑1
Fr*dr
(5) a)
F→=const
α=const
(5)→A1,2=
2∑1
Fr*dr
= 2∑1
F*dr*cosα
=F*
cosα
2∑1
dr=F*S*
cosα
N=dA/dt – производная работы по времени.
N=dA/dt=(F→*dr→)/dt=F→*U→=F*U*cosα
(6) Wк
различных тел. T=
mU2/2
(1) 2)T=N∑i=1Ti=N∑i=1
iV2/2
(2) 3) U=ωR
dT=U2dm/2=ω2l2dm/2
Tвр=∑dT=∑(ω)2l2dm/2=Izω2/2
Tвр=Izω2/2
(3) T= mU2/2
сложное движение твёрдого тела.
сложное=пост+вращ
T= mU2/2
+Iω2/2
(4)
13.Работа силы при вращении.
d
 t→dI→dS=r*dI
α=90-β dA=F*dS*cosα=M*dI
dA=M*dI (1)- элементарная работа силы A1,2=φ2
∑φ1
dφ= φ2
∑φ1
M* dφ (2)
t→dI→dS=r*dI
α=90-β dA=F*dS*cosα=M*dI
dA=M*dI (1)- элементарная работа силы A1,2=φ2
∑φ1
dφ= φ2
∑φ1
M* dφ (2)
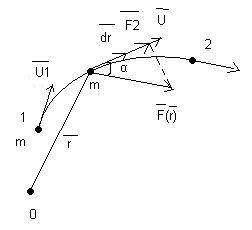
14.Потенциальная энергия в поле силы.
Е![]()
![]()

 сли
в каждой точке пр-ва задано знач-е
какой-либо величины, то говорят что
задано поле этой величины. T=T(x,y,z)
задано скаляр-е поле. Вект Ex=вект E(x,y,z),
вект E(Ex,Ey,Ez)
(рис 1). Существ такие силы консерват.
Работа консерват сил по перемещ тела
из 1-го полож во второе не зависит от
формы траектории и по любой траект-ии
одинаково. Aконс1a2=Аконс1б2.
Аконсф=Аконс1а2+Аконс2б1=Аконс1а2–Аконс1б2=0
все функиона-ые силы
(электрич,магн,гравитационн,ядерные)-все
консерват.неконс-ая силу-сила трения.
Для тела в поле только консерват силы
можно ввести понятие Wпотенциальной.
П=П(r)=П(x,y,z)
в этом поле наша мат точка имеет только
Wпот(П)
которая зависит только от положения.
Алгоритм введения П: 1) выбираем нулевой
уровень П-произвольно 2) выбираем произв
траектория переноса тела потенц силы
в данную точку пр-ва. П тела в данной
точке с координ (x,y,z)
будет равна –Аконс
силы по переносу тела с 0 уровня в данную
точку пр-ва. П(r)=-Aконсp-r=p∫r
вект Fdr=
-p∫rFrdr
(3)-определ П в точке консерват силы-основа
расчета П в поле консерв F. Абсолютное
знание П зависит от выбора нулевого
уровня. Рис(3) Аб12=А1р+Ар2=(-Ар1)+Ар2=П1-П2,
Аа12=Аб12=-(П2-П1)=-∆П
(4) при расчете А12
нет необходимости от выбора 0 уровня и
не зависит от 0 уровня. Т.к Аа12
не зависет от выбора 0 уровня, то и ∆П
не зависет от выбора 0 уровня. ∆П=-Аконс,
П2-П1=-Аконс12
(4)-второй
энергетический закон. Изменение П тела
равно миним А конс сил в поле П введена,
по перемещ тела из одного полож во
второе. П у тела столько, сколько и полей
консерв сил на нее действ.
сли
в каждой точке пр-ва задано знач-е
какой-либо величины, то говорят что
задано поле этой величины. T=T(x,y,z)
задано скаляр-е поле. Вект Ex=вект E(x,y,z),
вект E(Ex,Ey,Ez)
(рис 1). Существ такие силы консерват.
Работа консерват сил по перемещ тела
из 1-го полож во второе не зависит от
формы траектории и по любой траект-ии
одинаково. Aконс1a2=Аконс1б2.
Аконсф=Аконс1а2+Аконс2б1=Аконс1а2–Аконс1б2=0
все функиона-ые силы
(электрич,магн,гравитационн,ядерные)-все
консерват.неконс-ая силу-сила трения.
Для тела в поле только консерват силы
можно ввести понятие Wпотенциальной.
П=П(r)=П(x,y,z)
в этом поле наша мат точка имеет только
Wпот(П)
которая зависит только от положения.
Алгоритм введения П: 1) выбираем нулевой
уровень П-произвольно 2) выбираем произв
траектория переноса тела потенц силы
в данную точку пр-ва. П тела в данной
точке с координ (x,y,z)
будет равна –Аконс
силы по переносу тела с 0 уровня в данную
точку пр-ва. П(r)=-Aконсp-r=p∫r
вект Fdr=
-p∫rFrdr
(3)-определ П в точке консерват силы-основа
расчета П в поле консерв F. Абсолютное
знание П зависит от выбора нулевого
уровня. Рис(3) Аб12=А1р+Ар2=(-Ар1)+Ар2=П1-П2,
Аа12=Аб12=-(П2-П1)=-∆П
(4) при расчете А12
нет необходимости от выбора 0 уровня и
не зависит от 0 уровня. Т.к Аа12
не зависет от выбора 0 уровня, то и ∆П
не зависет от выбора 0 уровня. ∆П=-Аконс,
П2-П1=-Аконс12
(4)-второй
энергетический закон. Изменение П тела
равно миним А конс сил в поле П введена,
по перемещ тела из одного полож во
второе. П у тела столько, сколько и полей
консерв сил на нее действ.
15 .Потенциальная энергия тела в поле тяжести на малых высотах.
Т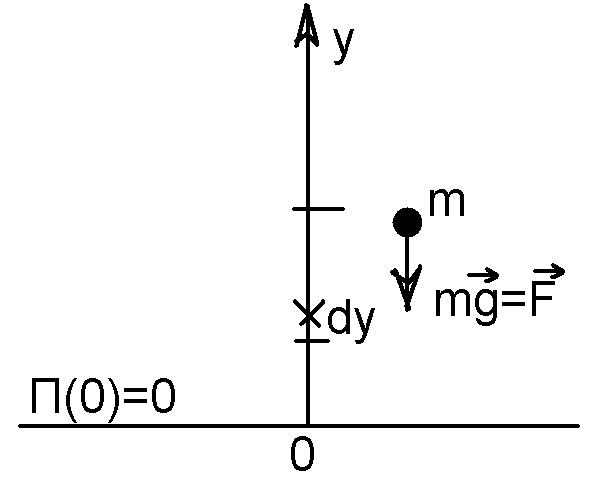 .к
mg-консерват сила, тело имеет П. П(y)-?.
1) П(y=0)=0
2) (3)( П(r)=-Aконсp-r=p∫r
вект Fdr=
-p∫yFrdr)→П(y)
→-p∫rFydy=mg-p∫ydy=mgy.
Y-высота
тела над нулевым уровнем.
П(y)=mgy→(5(F=-((δП/δx)i+(
δП/
δy)j)+(
δП/
δz)k)
▼-векторный оператор Набла.
▼=(δ/δx)i+(δ/δy)j)+(δ/δz)k))→Fy=-▼П=-▼П=-dП/dy=-(d/dy)(mgy)=-mg
.к
mg-консерват сила, тело имеет П. П(y)-?.
1) П(y=0)=0
2) (3)( П(r)=-Aконсp-r=p∫r
вект Fdr=
-p∫yFrdr)→П(y)
→-p∫rFydy=mg-p∫ydy=mgy.
Y-высота
тела над нулевым уровнем.
П(y)=mgy→(5(F=-((δП/δx)i+(
δП/
δy)j)+(
δП/
δz)k)
▼-векторный оператор Набла.
▼=(δ/δx)i+(δ/δy)j)+(δ/δz)k))→Fy=-▼П=-▼П=-dП/dy=-(d/dy)(mgy)=-mg
П![]()
![]()
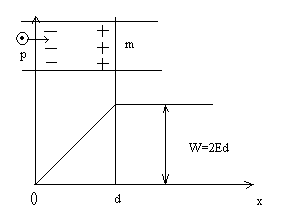 П объекта в зависим-ти от координат наз
энергетической диаграммой. Создает
потенциальн барьер для перехода из
10-ои точки на горку. W-высота
барьера. Если E>W, то лыжник падает в
зону 2, если то E<W нет. Система стремится
в сост, где ега П минимальн . в точках
экстремума П полож равновесия. В точках
min-устойчивое, в точках max-неустойчивое.
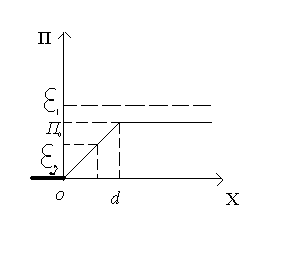
Пример 2. П заряда в однородном электрич
поле (плоский конденсатор)F=qE
(E=const),
П=П(x)-?.
P-носители-носитель
заряда – свободные электроны. Диффузия
свободных электронов. Дырка в таком
поле имен П. электрич сила консерват.
Решение:1) П(0)=0 2) (3) →П(x)=-0∫xFxdx=qEo∫xdx=qEx,
0≤x
≤ d,
П(d)=q(Ed)=П0=qVп,
q=1,6*10-19
Кл, Vп-понтантная
разность потенц, кот возникает на
р-переходе. Если E1>П0-проскочит
барьер, E1<П0-нет
П объекта в зависим-ти от координат наз
энергетической диаграммой. Создает
потенциальн барьер для перехода из
10-ои точки на горку. W-высота
барьера. Если E>W, то лыжник падает в
зону 2, если то E<W нет. Система стремится
в сост, где ега П минимальн . в точках
экстремума П полож равновесия. В точках
min-устойчивое, в точках max-неустойчивое.
Пример 2. П заряда в однородном электрич
поле (плоский конденсатор)F=qE
(E=const),
П=П(x)-?.
P-носители-носитель
заряда – свободные электроны. Диффузия
свободных электронов. Дырка в таком
поле имен П. электрич сила консерват.
Решение:1) П(0)=0 2) (3) →П(x)=-0∫xFxdx=qEo∫xdx=qEx,
0≤x
≤ d,
П(d)=q(Ed)=П0=qVп,
q=1,6*10-19
Кл, Vп-понтантная
разность потенц, кот возникает на
р-переходе. Если E1>П0-проскочит
барьер, E1<П0-нет
16.Потенциальная энергия заряда в однородном электрическом поле.
(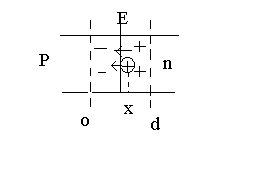 плоский
конденсатор) F=q·E
(E=const)
П=П(x)
? В P
носители – дырки В n
свободные электроны Дырка имеет потенц.
Энергию т.к. сила косерват. Найти П(х);
Решение П(0)=0
плоский
конденсатор) F=q·E
(E=const)
П=П(x)
? В P
носители – дырки В n
свободные электроны Дырка имеет потенц.
Энергию т.к. сила косерват. Найти П(х);
Решение П(0)=0
![]() П(х)=-
П(х)=-![]() =qE(
=qE(![]() )=qE
)=qE![]()
![]() (для внутр. поля) П(d)=q(Ed)=П
(для внутр. поля) П(d)=q(Ed)=П![]() =qV
=qV![]() q=1,6·10
q=1,6·10![]() Кл
V
- внутренняя контактная разность
потенциалов возникающая внутр.
Кл
V
- внутренняя контактная разность
потенциалов возникающая внутр.
17.отенциальная энергия заряда в поле точечного заряда.
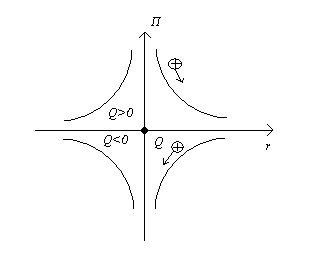
![]() Q-покоится
(источник поля)
Q-покоится
(источник поля)
![]()
![]()
З![]() аряд
q
имеет потенц. энергию в эл. Поле заряда
Q
т.к. сила Кулона – консерв. П
аряд
q
имеет потенц. энергию в эл. Поле заряда
Q
т.к. сила Кулона – консерв. П![]() (r)
=? Решение:1) П(
(r)
=? Решение:1) П(![]() )
=0 Нулевой уровень на
2)
П
(r)=
)
=0 Нулевой уровень на
2)
П
(r)=
![]() =
=![]() =
=![]() =
=![]()
![]() =
=![]() (
(![]() )
)![]() =
=![]() П
(r)=
П
(r)=
Работа выхода
электрона из металла. А выхода
![]() из Ме
из Ме
![]() -выскочит
-выскочит
![]() -нет
-нет
![]()
![]()
18 закон изменения механической энергии частицы.
1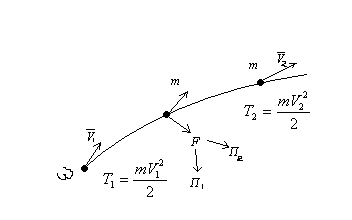 9.закон
сохранения механической энергии.
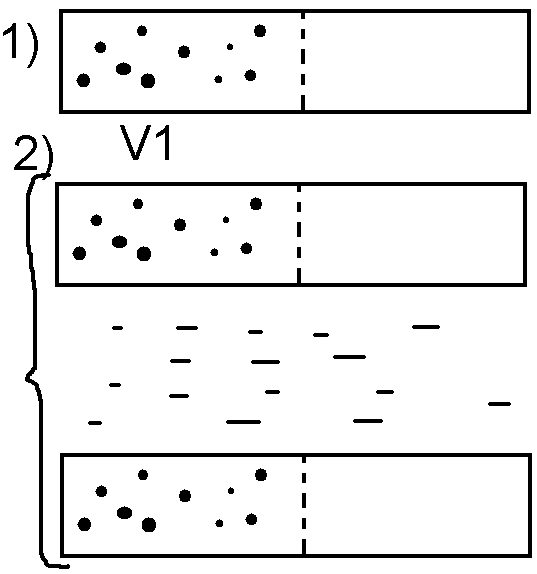
Прохождение частицы через потенциальный
барьер (дырка в P-N переходе)
9.закон
сохранения механической энергии.
Прохождение частицы через потенциальный
барьер (дырка в P-N переходе)
З-н изменения кинетической энергии.
![]()
![]()

![]() Е=Т+П
Е=Т+П
![]() Изменение механической энергии тела(сист.
тел) =работе консерв. сил (сила трения,
сопротивления) над телом. а)
Изменение механической энергии тела(сист.
тел) =работе консерв. сил (сила трения,
сопротивления) над телом. а)
![]() т.е. все силы сист. назыв. консерв. в
которых действ. только консерв. силы.
т.е. все силы сист. назыв. консерв. в
которых действ. только консерв. силы.
![]() -
закон сохранения потенциальной
механической энергии или системы. Закон
сохранения механической энергии. Мех.
энергия тела (системы) на которую действ.
только консерв. силы сохр. Для
сохранения механической энергии. Пример:
Дано: р-n
переход В поле на дырку действ. только
электрич сила. Полная механическая
энергия.
-
закон сохранения потенциальной
механической энергии или системы. Закон
сохранения механической энергии. Мех.
энергия тела (системы) на которую действ.
только консерв. силы сохр. Для
сохранения механической энергии. Пример:
Дано: р-n
переход В поле на дырку действ. только
электрич сила. Полная механическая
энергия.
![]()
![]()
![]() →
→
![]()
![]() ,
,
![]()
![]()
