8. Основное уравнение динамики вращательного движения твердого тела вокруг н еподвижной оси.

( вектор dl/dt)=вектор M(Ур-ия движение мат точки относит центра). Отдельная точка вращ по окр пост R. dm→(I_z=mR² момент инерции мат точки относит z)→dI_z=R²dm б) I_zE=M_z, I_z=const. dI_zE_z=IM_{z внутр} +IM_{z внешн}| ∫..→ E(∫dI_z)=∑M_{z внутр} + ∑ M_{z внешн} (А) I_z=∫dI_z=_m∫R²dm (1)-момент инерции твердого тела относит оси z. Определ момента инерции тв тела: z: I_zE=M_z (2)-основное Ур-ие динамики вращат движуния вокруг неподвижной оси (проход через центр тяжести) (2) исп при решении задач. Справедливо на ось вращ (В) →dL_z/dt=M_z (3), (2) →I_z(dw/dt)=M_z (I_z=const) (d(I_zw))/dt=M_z (2^|) из (2^|) и (3) следует L_z=I_zw Для симмм тв тела , вращающ вокруг неподвижной оси симметрии, можно показать что L направлен в сторону w. Вектор L=I вектор w (4)-связь момента импульса и угловой ск-ти симметр тв т.

8. закон сохранения момента импульса. Эксперименты на скамье Жуковского.

Г ироскоп. 1)на карданном вале. Если на ось не лдейств внешн силы, то она сохран свое направление.(1) вектор dl/dt=вектор M-момент внешних сил. вект L=вект L₁+вектL₂, вект L^|=вект L^|₁+вектL^|₂ a) вект M=0→dL/dt=0 → вект L=const-закон сохран момента импульса системы. Если ∑ моментов внешних сил,дейст на вращ тел =0, то момент импульса системы сохран. вект L=вект L^| 1) до вект L=вект L_ч-c+вект L_r→вект L=I_ч-cw₁+I_rw₁, после вект L^|=вект L^|_ч-c+вект L^|_r→вект L^|=I^|_ч-cw2+I^|_rw₂. L^*=(I_ч-c+2mr²)вект w₁=(З.С.М.И)=вект L=(I_ч-c+0)w₂, w₂=((I_ч-c+2mr²)/I_ч-c)w₁ →|w₂|>|w₁| 2) до: ч-с+обруч. вект L=вект L_ч-c+вект L_обруч L=0+0.после: вект L^|=вект L^|_ч-c+вект L^|_обруч , L^|=I_ч-cw₂+I_обрw₁

По З.С.М.И вект L=L^|, I_ч-cw₂+I_обрw₁=0, w_ч=-(I_обр/I_ч-с)w₁ вращение человека противопол вращ обруча. I_обр/I_чел<<1, |w₂|<<|w₁| 3) ДО ч-с+обруч. вект L=вект L_ч-c+вект L_обр, вект L=0+I_обрw₁. ПОСЛЕ. вект L^|=вект L^|_ч-c+вект L^|_обр , вект L^|=I_ч-сw₂-I_обрw₁, по З.С.М.И вект L=0+I_обрw₁= вект L^|=I_ч-сw₂-I_обрw₁, I_обрw₁=I_ч-cw₂-I_обрw₁, w₂=(2I_обрw₁)/I_ч-с.

8. Моменты инерции простейших: тел мат точки, системы мат точек, однородного стержня. Теорема Штейнера (без доказательства)

1.мат точка. I_z=mR² (5)-момент инерции мат точки вокруг неподвижной оси.

2 .система мат точек. I_z=^N∑_n=1Iz_i=^N∑_n=1 m_iR_i² (6) момент инерции стержня относит оси вращения. I_z=_m∫R²dm.теорема Штейнера. (I=I₀+mR²)

3.Теорема Штейнера. Момент инерции.

• п 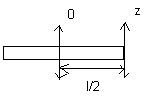озволяет зная относительно оси симметрии любой другой оси параллельной оси симметрии.

I₀'=I₀+ma²

I_z=I₀+m(l/)=ml²/12+ml²/4=ml²/3

8. гироскоп. Процессия.

Г 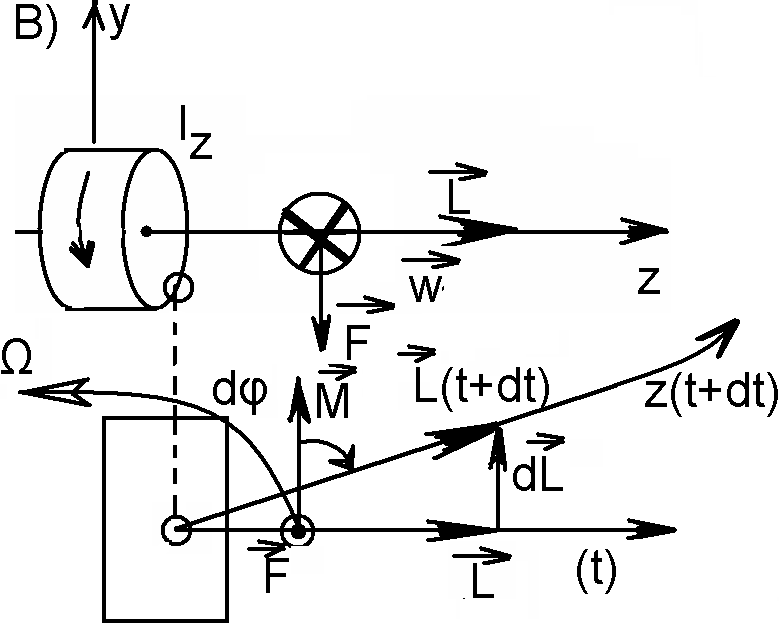ироскопы- быстровращающееся симметричное тв тело. Вект L=I_z вект w , вект dL/dt=вект M (1). Ось может перемещ, а центр неподвижен. А) M=0→(1)вект dL/dt=0→L=const. L-жестко связан с осью гироскопа, поэтому ось гироскопа сохран направление. гирокомпас, стабилиз направл.б) M||оси z, вект L.вект M_y=[вект r_y*F_y], M_y↑↑L, M_T↑↓L My-ускоряет вращение MT-тормозит вращение Эти моменты будут лишь менять w по величине, но не по направл. (1)→(d(I_zw))/dt=M→z: I_z(dw/dt)=M_y-M_T, dw/dt=E_z, I_zE=M_y-M_T, E_z=(M_y-M_T)/I_z-углов упт.вращ гироскопа, если M_y>M_T,то E_Z>0(ускорение) M_y<M_T→E_z<0. в) поведение вращ героскопа определ напр момента силы. Вект M+[вект r,F]. Пустьь момент времени t, M(t) следоват момент времени t+dt→вект L(t+dt). (t→L(t), t+dt→L(t+dt)) →dt→вект dL→L(t+dt)-L(t) → L9t+dt0=L(t)+dL. Ось гироскопа жестко связана с L, если мы узнаем направление L(t+dt), то зная положение оси в момент времени t, найдем её в момент времени (t+dt). dL/dt=M (1) →dL=Mdt→вект dL↑↑вект M. Ось за время dt, поверн на угол dφ вокруг вертик оси y. Ось гироскопа под действ такой силы будет вращ вокруг вертик оси. Дв-ие гироскопа наз прецессия. Ω_приц=dφ/dt=(1/L)(dL/dt)=из геометрии(dL=Ldφ-длина дуги окр с рад R кот поверн под углом dφ)=M/L. Ω_приц=M/L=(rF)/(I_zw)-угловая ск-ть прецессии.