1. Перемещение, скорость, ускорение. Тангенциальная и нормальная компоненты ускорения.

Рассмотрим в опр-й сис-ме коор-т XYZ движение мат-й точки. Положение точки опр-ся радиусом-вектором, направленным из начала координат в точку в момент времени t+Δt (Δt – небольшое конечное изменение времени). Δr^=r^ (t+Δt)-r^ (t). Скорость: υ^=Δr^/Δt (1). υ^- средняя скорость за время Δt. υ^||Δr^.

Если Δt устремляется к 0, то limΔt=dt при Δt0.

dt – бесконечномалое изменение времени.

limΔr^=dr^ при Δt0.

υ^= lim Δr^/Δt = dr^/dt (опр-е мгновенной скорости). (2)

r^=r^ (t). dr^=r^ (t+dt) - r^ (t). tt+Δt.

Скорость(мгновенная) – это производная радиуса вектора по времени. Производная ф-ии по времени опр-т скорость ее изменения.

t  υ^ (t) – в момент времени t. t+dt  υ^ (t+dt).

dt  dυ^ = υ^ (t+dt) – υ^ (t).

a^= dυ^/dt (3).

y’(x)=limΔy/Δx = Δy/Δx = dy/dx, при Δx0.

1)

a^=a_^+a_n^

a_^||υ^

a^=dυ^/dt a_n^υ^ a^=dυ/dt a_n=0, a=a_

a_=dυ/dt (4)

Модуль a_ - производная модуля скорости по времени.

Тангенциальное ускорение характеризует скорость изменения скорости по величине, но не по направлению.

Н ормальное ускорение характеризует изменение скорости по направлению, а не по величине.

2)

υ=const

a_=dυ/dt=0

a^=a_n^

a=a_n=υ²/R (5)

3)

В (5) R-радиус кривизны траектории – радиус окружности, касательной траектории.

a^=a_^+a_n^ a=√a_²+a_n²|=√(dυ/dt)²+(υ²/R)²| (6)

Перемещение

r ^ d/dt υ^ d/dt a^

1. Мат-я точка движется по координате x с υ=const. В начальный момент t₀=0, x₀. В момент времени t; x(t).

X=S+x₀=υt+x₀ S=υ*t

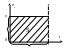
В осях υ_xt путь, пройденный точкой, численно равен площади фигуры под графиком.

2. Пусть υ≠const, а зависит от времени υ=υ(t).

x=S+x₀

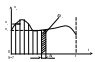
а) 0 ÷ t  разбиваем на N участков Δt; i=1÷t

б ) ΔS_i=υ_i*Δt_i; в) S≈ =ΔS_i= υ_i*Δt_i

г) S=lim υ_i*Δt_i= υ(t)dt (сумма БМ величин)

п ри N, Δt_i0

S= υdt υdt = dx

Весь интервал времени от 0 до t разбили на бесконечное число бесконечномалых интервалов dt. Каждый интервальчик dt умножается на скорость за это время и получаем элементарное перемещение (путь) за время dt.

υ=dx/dt  dx=υ*dt.

И нтеграл ф-ии дается площадью фигуры под графиком ф-ии.

x= υdt+x₀^; r^= υ^dt+r₀^; υ^dt = dr^;

υ^dt – полное перемещение.

υ^=dr^/dt  dr^=υ^dt

Δ r^=r^-r₀^  r^=Δr^+r₀^ (7)

υ^= a^dt + υ₀^; a^dt = Δυ^; a^dt = dυ^. (8)

a^=dυ^/dt  dr^=a^dt; Δυ^=υ^-υ₀^  υ^= Δυ^+υ₀^

2. Угол поворота, угловая скорость, угловое ускорение. Связь линейных и угловых характеристик.

Д ано: твердое тело вращ-ся вокруг неподвижной оси z.

1. Положение каждой точки твердого тела опр-ся углом поворота, как функция времени φ=φ(t). Угол поворота одинаков для всех точек.

2. Пусть в момент времени t, положение точки определяется φ(t). t+dt  φ(t+dt)-φ(t). Тогда за время dt тело повернется на dφ  БМ изменение угла.

dφ=φ(t+dt)-φ(t) ω=dφ/dt (1)

У гловая скорость – отношение бесконечно малого угла поворота к бесконечно малому промежутку времени. Угловая скорость – это производная от угла поворота по времени. Угловую скорость удобно считать вектором. Направление угловой скорости – по оси вращения и связана с вращением правилом правого винта.

Вращая правый винт по вращению тела, он вкручивается по угловой скорости.

3. Быстроту изменения угловой скорости характеризует угловое ускорение.

Д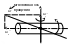 ано: имеется вращающееся тело в момент вр-ни t; ω(t).

Такое движение можно представить как вращение в каждый момент времени, как вращение вокруг мгновенной оси вращения.

В момент времени t+dt: ω^ изменилась и стала ω^(t+dt). Тогда за время dt угловая скорость изменилась на ω^(t+dt)-ω^(t).

ε ^=dω^/dt [с^-2] (9)

Ускорение – это производная от угловой скорости.

а) если ось неподвижна, то угловое ускорение ε^↑↑dω^ - тело ускоряет вращение.

б) вращение замедляется ε^↑↓dω^.

φ d/dt ω^ d/dt ε ^

φ = ωdt + φ₀; ωdt – Δφ; ωdt – dφ (10)

ω =dφ/dt  dφ=ωdt; φ=Δφ+φ₀; Δφ=φ - φ₀

ω^= ε^dt + ω₀^; ε^dt - Δω^; ε^dt - dω^. (11)

Δω^=ω^-ω₀^

С вязь линейных и угловых характеристик вращения.

Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижных осей. Угловая скорость ω всех точек тодинакова. Линейные будут различны.

R=r*sinα Пусть за время dt тело повернулось на угол dφ и прошло путь dS. dt  dφ  dS dS=R*dφ |: dt

dS/dt=R*(dφ/dt)  υ=R*ω υ=ω*R

υ=ω*R=ω*r*sinα – связь между модулями υ, R, r, ω. (12)

υ^ω^, R^; υ^ω^, r ^;

υ^=ω^×R^=ω^×r^ (13)

(12) и (13) – формулы связи одной и той же точки твердого тела.

Ускоренное вращение.

a_=dυ/dt; υ=ωR |: d/dt

dυ/dt=(dω/dt)*R

a_=ε*R (14)

a_n=υ²/R=ω²*R (15)

a^=a_^+a_n^

a=√ a_+a_n| = R√ε² + ω⁴| (16)