Примеры. Число: -1.
Код модуля числа: 0 0000001.
Обратный код числа: 1 1111110.
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Число: -127.
Код модуля числа: 0 1111111.
Обратный код числа: 1 0000000.
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3.Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Примеры. Дополнительный код числа –1:
-
1
1
1
1
1
1
1
1
Дополнительный код числа -127:
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемешаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Как компьютер выполняет арифметические действия над целыми числами.
Сложение и вычитание. В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение уменьшаемого с обратным или дополнительным кодом вычитаемого.
При сложении обратных кодов чисел А и В имеют место четыре основных и два особых случая. Рассмотрим их.
Случай 1. А и В положительны. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Приведем пример.
Десятичная запись: Двоичные коды:
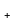3
0
0000011
7
0 0000111
10 0 0001010
Получен правильный результат.
Случай 2. А положительное, В отрицательное и по абсолютной величине больше, чем А. Приведем пример.
Десятичная запись: Двоичные коды:
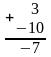
Обратный
код числа -10
Обратный код числа -7
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируется: 1 0000111 = -7 .
Случай 3. А положительное, В отрицательное и по абсолютной величине меньше, чем А. Приведем пример.
Десятичная запись: Двоичные коды:
Обратный
код числа - 3
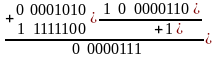
Компьютер исправляет полученный первоначально не правильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.
Случай 4. А и В отрицательные. Приведем пример.
Обратный
код числа - 3
Обратный
код числа - 10
Обратный
код числа - 7
Полученный
первоначально неправильный результат
(обратный код числа -11
вместо обратного кода числа -10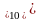
)
компьютер исправляет переносом единицы
из знакового разряда в младший разряд
суммы. При переводе результате в прямой
код биты цифровой части инвертируется:
1 0001010 = -10
.
При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещение о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения.
Случай
5. А и В положительные, сумма А и В больше
либо равна 2
,
где n
– количество разрядов формата чисел
(для однобайтного формата n=8,
2 =2 =128). Приведем пример.
Десятичная запись: Двоичные коды:
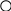
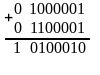Переполнение
Семи разрядов цифровой части числового формата недостаточно для разрешения восьмизначной суммы (162 =10100010 ), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака и знаков слагаемых, что является свидетельством переполнения разрядной сетки.
Случай 6. А и В отрицательные, сумма абсолютных величин А и В больше либо 2 . Приведем пример.
Десятичная запись: Двоичные коды:
Переполнение
Обратный
код числа - 63
Обратный
код числа - 95
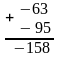
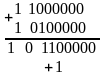
Здесь знак суммы не совпадает со знаком слагаемых, что свидетельствует о переполнении разрядной сетки.
Все рассмотренные случаи имеют место и при сложении дополнительных кодов чисел.
Контрольные вопросы
Что понимают под системой счисления?
Какие существуют системы счисления?
Что такое позиционная система счисления?
Что такое основание системы счисления?
Сформулируйте правило перевода из одной позиционной системы счисления в другую.
Сформулируйте правило перевода из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления.
Запишите правила выполнения арифметических действий в двоичной системе счисления.
Как представляются целые числа без знака в однобайтном (в двухбайтовом) формате?
Как представляются целые числа со знаком?
Что такое прямой код?
Что такое обратный код?
Что такое дополнительный код?
Как связаны прямой, обратный и дополнительный коды?
Какие случаи возможны при выполнении компьютером арифметических действий над целыми числами?
МНОЖЕСТВА
ЗАДАНИЕ МНОЖЕСТВ
Интуитивное определение множества. Множество – это собрание определенных и различных между собой объектов, мыслимое как единое целое. Эти объекты называются элементами множества.
В этом определении собрание предметов рассматривается как один объект, как единое целое. Примеры множеств:
1) множество студентов в данной аудитории;
2) множество целых положительных чисел меньших 10;
3) множество решений уравнения x2-1=0;
4)
множество чисел Фибоначчи:
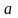1,
2,
3,….,
где
k+2=
k+
k+1,
k≥1,
1=
2=1;
5) множество самолетов и авиапассажиров.
Если
объект (элемент) х принадлежит множеству
М, то записываем х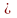
М
, если же х не является элементом из М,
то х
М.
Отношение
называется отношением принадлежности.
То, что множество М состоит из элементов 1, 2, … n, записывает с помощью фигурных скобок: М={ 1, 2, … n}.
Введем понятие предиката и порождающей процедуры.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
B
A
или
множества В:
A B={x: x А или х В}.
На рис. 1.1 множество А В заштриховано. рис 1.1
Пересечение множеств А и B называется множество
A B, элемент которого являются элементами обоих множеств
А
и В: A
B
={x: x
А
или х
В}.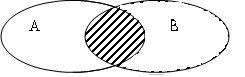 
Рис. 1.2
На рис. 1.2 множество А В заштриховано.
Разность множеств А и В: - А\В
A
B
Рис. 1.3
На рис. 1.3 множество А\В заштриховано.
С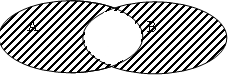
имметричная
разность множеств А и В: - А
В
А В=(А В)\(А В) ={x: (x А и х В) или (x В и х А)}. Рис. 1.4
На рис 1.4 множество А В заштриховано
U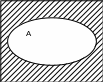
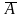=СА{х:
х
А}
Предполагается, что существует (универсальное)
множество U, такое, что А U. На рис 1.5
множество
заштриховано.
рис 1.5
СВОЙСТВА ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ