Лабораторная работа № 6

Цель: Решение транспортной задачи.

Транспортная задача является классической задачей исследования операций. Множество задач распределения ресурсов сводится именно к этой задаче.

Постановка задачи

Логистическая компания обслуживает четыре магазина, доставляя в них товары определенной группы с шести складов. Потребность каждого магазина в товарах различна. Запасы на каждом складе ограничены. Требуется определить, каким образом следует организовать маршрут доставки товаров, чтобы грузооборот был минимальным. Другими словами, решить, с какого склада, в какой магазин и сколько перевозить товаров для минимизации грузооборота перевозок.

Исходные данные следующие.

Таблица 1. Наличие товаров на складах

Номер склада	Наличие товаров, ед.
Склад № 1	2000
Склад № 2	1300
Склад № 3	1700
Склад № 4	1550
Склад № 5	1000
Склад № 6	1450

Таблица 2. Потребность магазинов в товарах

Номер магазина	Потребность в товарах, ед.
Магазин № 1	2000
Магазин № 2	1500
Магазин № 3	2100
Магазин № 4	3400

Таблица 3. Расстояния между складами и магазинами

	Магазин № 1	Магазин № 2	Магазин № 3	Магазин № 4
Склад № 1	6	4	5	11
Склад № 2	12	6	4	9
Склад № 3	15	8	10	4
Склад № 4	9	5	11	6
Склад № 5	3	7	12	11
Склад № 6	4	9	15	12

1. Подготовим исходные данные. В строку C3:F3 занесем потребности магазинов в товарах. В столбец В4:В9 занесем данные о наличии товаров на складах. В блок ячеек C4:F9 занесем расстояния между складами и магазинами.

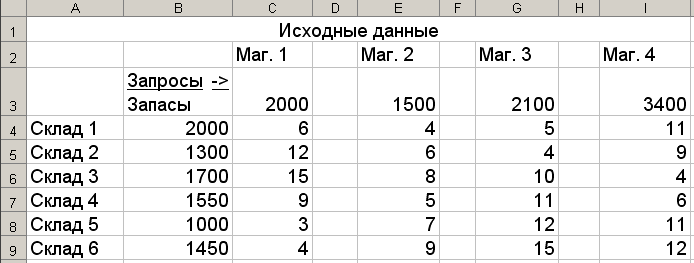
Данная задача является замкнутой транспортной задачей, поскольку общее количество товаров на складах равно суммарной потребности в них всех магазинов.

Решение задачи методом потенциалов

1. Строим исходный опорный план методом минимального элемента. Для удобства расчетов создаем таблицу следующей структуры:

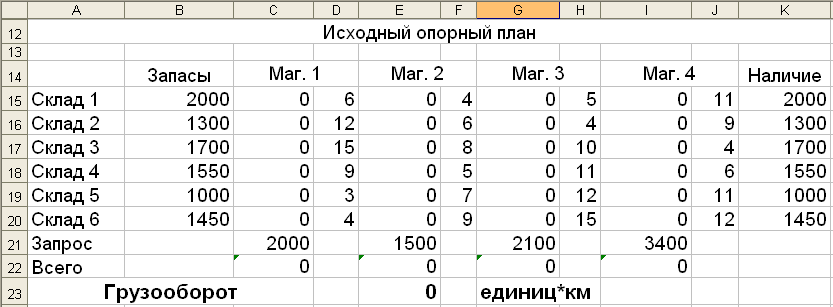
Столбцы, содержащие информацию о запросах магазинов, разделяем на две части:

• В первом столбце будем записывать количество единиц товара, привезенного в этот магазин с одного из складов. Перед началом создания исходного плана эти столбцы обнуляем. В строку Запрос заносим потребность данного магазина в товарах из исходных данных.

• Во второй столбец заносим расстояния между магазинами и складами из исходных данных. В строку Запрос заносим признак, который будет сигнализировать выводом знака плюс об удовлетворении потребности данного магазина в товарах в процессе формирования исходного плана. Если в магазин еще надо завозить товар, то соответствующая ячейка будет пустой. В начале формирования плана все эти ячейки, естественно, будут пустыми. Формула для создания такого алгоритма работы, например, для магазина 1 имеет вид:

С21 = ЕСЛИ(C15+C16+C17+C18+C19+C20=C21;"+";" ")

В строке Всего будем подсчитывать грузооборот между каждым магазином и складами, с которых завозится товар. Грузооборот представляет собой произведение количества перевезенного товара на расстояние перевозки. Это означает, что для магазина 1 грузооборот может быть вычислен по формуле:

С22 = СУММПРОИЗВ(C15:C20;D15:D20)

Для других магазинов грузооборот вычисляется аналогично.

В ячейке Е33 будем считать суммарный грузооборот по формуле:

Е23 = СУММ(C22:I22)

В столбце К будем вычислять текущее количество товара на соответствующем складе, равное запасу товара минус то его количество, которое перевезено во все магазины. Например, для склада 1 оно вычисляется по формуле:

К15 = =B15-C15-E15-G15-I15

2. Построение начинаем с ячейки, содержащей минимальное значение расстояния между складом и магазином – D19. Заносим в ячейку С19 значение х51=min(1000, 2000)=1000. В ячейке К19 появилось нулевое значение. Это означает, что строка 19 (Склад 5) закрыта.

Далее переходим к ячейке D20, т.к. в ней находится минимальное значение в столбце D. Заносим в нее значение х61=min(2000 - 1000, 1450)=1000. В ячейке D21 появился плюс, значит, столбцы D:С (Магазин 1) закрыты. Запросы первого магазина обеспечены в полном объеме, при этом на складе 6 осталось еще 450 единиц товара.

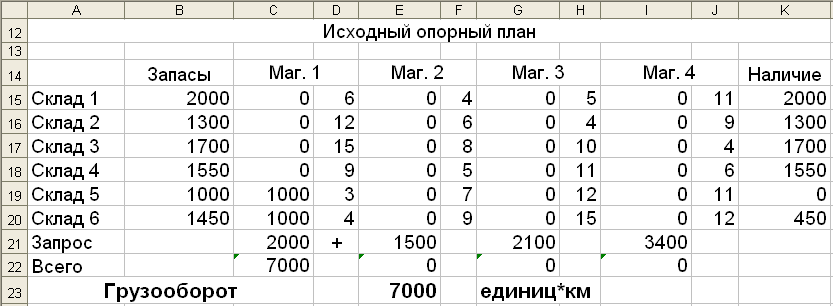
Продолжаем заполнение ячеек аналогичным образом.

Переходим к ячейке F20 и заносим в Е20 значение х62=min(1500, 1450 - 1000)=450. Строка 20 закрыта.

Переходим к ячейке F15 и заносим в нее значение х12=min(1500 - 450, 2000)=1050. Знак плюс в ячейке F21 говорит о том, что столбцы F:E закрыты.

Переходим к ячейке G15 и заносим в нее значение х13=min(2100, 2000 - 1050)=950. В ячейке К15 – ноль, значит, строка 15 закрыта.

Переходим к ячейке G16 и заносим в нее значение х23=min(2100 - 950, 1300)=1150. Столбцы G:H закрыты.

Переходим к ячейке I16 и заносим в нее значение х24=min(3400, 1300 - 1150)=150. Поскольку остался единственный незакрытый столбец, закрываем его строками 17 и 18.

Опорный план построен. Столбец К содержит одни нули, т.е. весь товар со всех складов вывезен. В столбцах D, F, H, J изображены плюсы, значит, запросы всех магазинов удовлетворены.

Грузооборот при реализации найденного плана составляет 42050 единиц*км.

3. Для построения первой итерации скопируем исходный опорный план, начиная со строки 27. В строке Запрос в столбцах, содержащих расстояния между магазинами и складами, запишем потенциалы магазинов: v₁, v₂, v₃, v4.

В столбце К запишем потенциалы складов от u₁ до u₆.

В блоке А42:А50 записываем систему уравнений для нахождения потенциалов, т.е. уравнения u_i + v_i = c_ij для всех свободных переменных. Получилось 9 уравнений и 10 неизвестных. Одно неизвестное полагаем равным нулю, например, v₁ = 0. Тогда из первого уравнения u₅ = 3, из второго – u₆ = 4, и так далее. Записываем найденные значения в столбцы В и С.

Вычисляем косвенные расстояния для всех свободных переменных и заносим их в столбцы F и G. Косвенная стоимость вычисляется по формуле: c_ij^’ = u_i + v_i. Например, для значения с₁₁ (ячейка G41): с₁₁^’ = u₁ + v₁. (G41=C44+C41).

Вычисляем разности d_ij = c_ij – c_ij^’ косвенные стоимости для всех свободных переменных и заносим их в столбцы H и I. Здесь c_ij – это реальные расстояния между складами и магазинами, а c_ij^’ – косвенные расстояния. Например, разность d₁₁ (ячейка I41) равна d₁₁ = c₁₁ – c₁₁^’ (I41= D30-G41).

Среди разностей есть отрицательные значения, следовательно, план можно улучшить, увеличив количество перевозимого товара на одном из этих направлений. Поскольку все отрицательные разности одинаковые, выберем любую из них, например, d52 и составим цикл пересчета. Для этого скопируем часть таблицы первой итерации в блок ячеек К41:Т47. Допустим, х₅₂ = А. Компенсируем увеличение х₅₂ уменьшением х₆₂: х₆₂ = х₆₂ - А. Далее компенсируем х₆₁, а затем – х₅₁. Цикл замкнулся. Следовательно, А=450, т.е. значение х₅₂ можно увеличить до 450. Изменяем значения, участвующие в цикле пересчета, в таблице первой итерации. Видим, что грузооборот стал меньше, т.е. решение стало ближе к оптимальному. Продолжая итерации, можно придти к оптимальному решению.