27.Показатели и формы распределения

Однородные сов-ти хар-ся как правило одновременными распределениями. Многовершинность свидетельствует о неоднородности совокупности. Появление 2-х и более вершин говорит о необходимости перегруппировки совокупности с целью выявления более однородных групп. Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисления показателей асимметрии и эксцесса.

Симметричными называются распределения в которых частота любых 2-х вариант равностоящих в обе стороны от центра распределения равны между собой (рис.) для симметричных соотношений вычисляется соотношение:   чем больше расхожа x ̅ и M₀ тем больше ассиметрия.

 G – самый больший показатель ассиметрии. Положения всемирно указывают на наличие правосторонней ассиметрии(правая ветвь длинее левой)

При значении |A_s | - 0,25 ассиметрия считается незначительной. |A_s | - 0,5 – значительной.  Более точный показатель распределения ассиметрии основан на показатели, кот. наз. моменты распределения. Момент распределения, k-го порядка – это среднее отклонение k-й степени от некоторый велечены A (постоянная величина).

Если A производное число, то моменты называются условными, если A=0, то моменты называются начальными.

то М называется центральными

   - начальный момент.

Наиболее точный показатель асимметрии основан на определённых центральных моментах 3-го порядка, т.е. нормированный момент 3-го порядка при нормальном распределении, т.е. соответствующие моменты =0. Оценка осуществляемости с помощью среднеквадратичной ошибки.

то ассиметрия признается существенной. Для ассиметрии распределений расчитывается показатель эксцесса. Эксцесс – это выпад эмпирического измерения вверх или вниз от вершины нормального распределения, определяется:

При нормальном распределении μ₄ = 3, Ex=0.

Существенность коэф-та эксцесса определяется аналогично. Существует и коэф-т ассиметрии рассчитывающий среднеквадратичную ошибку.

Если G_Ex>3, то коэф-т считается существенным.

Ex – выпад вершины вниз, т.е. распределение плосковершинное. Ex – выпад вершины вверх, распределение островершинное. Оценка существенности данных показателей ассиметрии и эксцесса позволяет сделать вывод о том можно ли отнести данное распределение к типу кривых нормального распределения.

28.Нормальное распределение и его свойства

При обработке данных измерений в науке и технике обычно предполагают нормальный закон распределения случайных погрешностей измерений. Оно всегда проявляется тогда, когда суммарная погрешность есть результат неучтенного совместного воздействия множества причин, каждая из которых дает малый вклад в погрешность. Причем совершенно неважно, по какому закону распределен каждый из вкладов в отдельности.

Свойства нормально распределенной случайной величины x:

 

1. ; 

 

2. ρ(x) является непрерывной функцией;

3. Центр распределения случайной величины одновременно является центром симметрии;

4. Малые отклонения встречаются чаще больших, другими словами, реализуются с большей вероятностью.

 

Соответствующее функциональное выражение для распределения задает формула Гаусса:

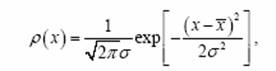, (1)

где σ² и – дисперсия и среднее значение распределения..

Вероятность того, что результат измерения попадет в интервал [x₁,x₂], равна:

 

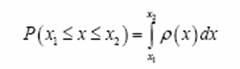 (2)

 

В скобках после P указано событие, для которого вычислена вероятность. При увеличении границ промежутка в обе стороны до бесконечности интеграл от функции распределения

 

 

 

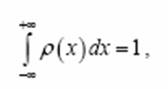
т.е. попадание результата измерения в диапазон является достоверным событием.

Пусть – произвольное отклонение от средней величины . Введем ε – величину отношения полуширины интервала ∆x к среднему квадратичному отклонению σ:

 

 

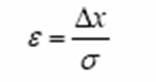
В таблице указана вероятность α:

 

         (4)

 

 Ее можно рассчитать по приближенному выражению:

 

 

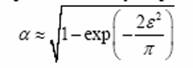        (5)

 

Полезно запомнить несколько чисел:

Таблица №1. Нормальное распределение Доверительные интервалы [x-∆x, x+∆x] для доверительной вероятности α (в долях ε).

 

α	0,68	0,90	0,95	0,990	0,997	0,999
ε	1,0	1,65	2,0	2,6	3,0	3,3

 

Правило «3 стандартов»

Видно, что результат измерения с вероятностью 68% попадет в интервал  , т.е. примерно каждое третье измерение даст результат за пределами этого интервала. За пределами интервала    окажется один результат из двадцати, а для интервала   – только один из трехсот. Значит, интервал ±3σ вокруг среднего значения является почти достоверным, так как подавляющее большинство отдельных результатов многократного измерения случайной величины окажется сосредоточенным именно в нем.

При обработке результатов эксперимента часто используется «правило 3σ», или правило «трех стандартов», которое основано на указанном свойстве нормального распределения. С учетом проведенного выше анализа, можно установить наличие промаха в результате отдельного измерения, а значит, отбросить его, если результат измерения более чем на 3σ отличается от измеренного среднего значения случайной величины.