26.Показатели размера и интенсивности вариации
Абсолютные средние размеры вариации
Следующим этапом изучения вариации признака в совокупности является измерениехарактеристик силы, величины вариации. Простейшим из них может служить размах илиамплитуда вариации -абсолютная разность между максимальным и минимальным значениямипризнака из имеющихся в изучаемой совокупности значений. Таким образом, размах вариациивычисляется по формуле
Поскольку величина размаха характеризует лишь максимальное различие значений признака,она не может измерять закономерную силу его вариации во всей совокупности.Предназначенный для данной цели показатель должен учитывать и обобщать все различиязначений признака в совокупности без исключения. Число таких различий равно числусочетаний по два из всех единиц совокупности; по данным табл. 5.6 оно составит: С^ = 10 153.Однако нет необходимости рассматривать, вычислять и осреднять все отклонения. Прощеиспользовать среднюю из отклонений отдельных значений признака от среднегоарифметического значения признака, а таковых всего 143. Но среднее отклонение значенийпризнака от средней арифметической величины согласно известному свойству последней равнонулю. Поэтому показателем силы вариации выступает не алгебраическая средняя отклонений, асредний модуль отклонений:
По данным табл. 5.6 средний модуль, или среднее линейное отклонение, по абсолютнойвеличине вычисляется как взвешенное по частоте отклонение по модулю середин интерваловот средней арифметической величины, т.е. по формуле
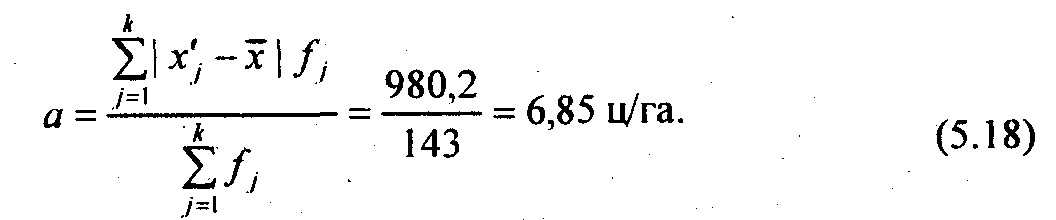
Это означает, что в среднем урожайность в изучаемой совокупности хозяйств отклонялась отсредней урожайности по области на 6,85 ц/га. Простота расчета и интерпретации составляютположительные стороны данного показателя, однако математические свойства модулей«плохие»: их нельзя поставить в соответствие с каким-либо вероятностным законом, в томчисле и с нормальным распределением, параметром которого является не средний модульотклонений, а среднее квадратическое отклонение (в англоязычных программах для ЭВМназываемое «the standard deviation», сокращенно «s.d.» или просто «s», в русскоязычных - СКО).В статистической литературе среднее квадратическое отклонение от средней величиныпринято обозначать малой (строчной) греческой буквой сигма (ст) или s (см. гл. 7):
для ранжированного ряда
для интервального ряда
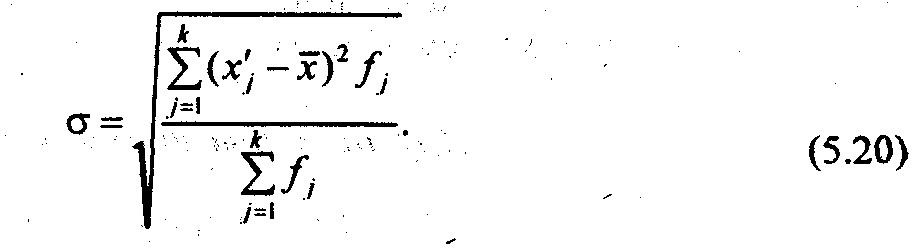
По данным табл. 5.6 среднее квадратическое отклонение урожайности зерновых составило:
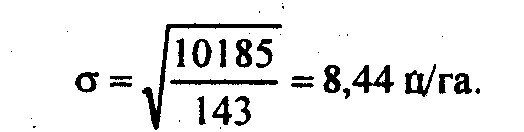
Следует указать, что некоторое округление средней величины и середин интервалов, напримердо целых, мало отражается на величине ?, которая составила бы при этом 8,55 ц/га.
Среднее квадратическое отклонение по величине в реальных совокупностях всегда большесреднего модуля отклонений. Соотношение (у : а зависит от наличия в совокупностях резких,выделяющихся отклонений и может служить индикатором «засоренности» совокупностинеоднородными с основной массой элементами: чем это соотношение больше, тем сильнееподобная «засоренность». Для нормального закона распределения ? : а = 1,2.
Понятие дисперсии
Квадрат среднего квадратического отклонения дает величину дисперсии ?2. Формуладисперсии:
простая (для несгруппйрованных данных):
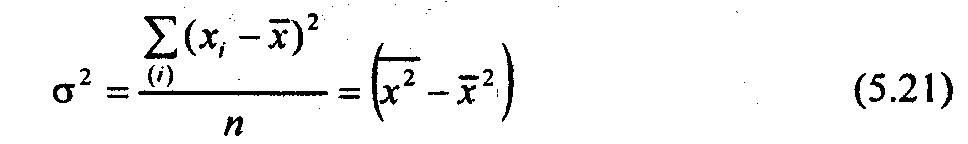
или
взвешенная (для сгруппированных данных):
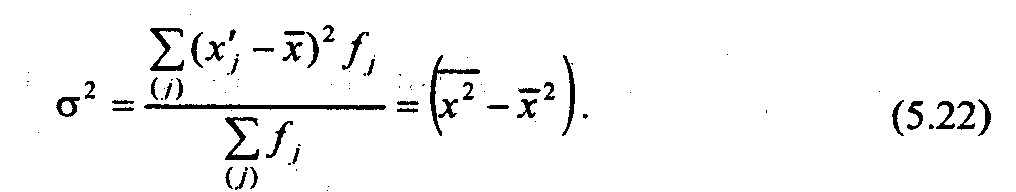
На дисперсии основаны практически все методы математической статистики. Большоепрактическое значение имеет правило сложения дисперсий (см. гл. 6).
Другие меры вариации
Еще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь вее центральной части, служит среднее квартцлъное расстояние, т.е. средняя величинаразности между квартилями, обозначаемое далее как q:
Для распределения сельхозпредприятий по урожайности в табл. 5.2
q = (36,25 - 25,09): 2 = 5,58 ц/га. Сила вариации в центральной части совокупности, какправило, меньше, чем в целом по всей совокупности. Соотношение между средним модулемотклонений и средним квартальным отклонением также служит для изучения структурывариации: большое значение такого соотношения говорит о наличии слабоварьирующего«ядра» и сильно рассеянного вокруг этого ядра окружения, или «гало» в изучаемойсовокупности. Для данных табл. 5.6 соотношение а: q = 1,23, что говорит о небольшомразличии силы вариации в центральной части совокупности и на ее периферии.
Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем болеедля разных признаков необходимы относительные показатели вариации. Они вычисляются какотношения абсолютных показателей силы вариации, рассмотренных ранее, к среднейарифметической величине признака. Получаем следующие показатели:
1) относительный размах вариации р:
2) относительное отклонение по модулю т:
3) коэффициент вариации как относительное квадратическое отклонение v:
4) относительное квартальное расстояние d:
где q - среднее квартильное расстояние.