
- •1.Понятие и общее представление о статистике.
- •2.Предмет, метод и задачи статистики.
- •3.Сущность сводки и группировки статистических данных.
- •4.Виды группировок.
- •5.Статистические ряды распределения.
- •Закономерности распределения
- •Общие понятия о статистических таблицах
- •Виды статистических таблиц
- •Основные правила составления и анализа статистических таблиц
- •7.Статистическое наблюдение: формы, виды, и способы.
- •Этапы статистического наблюдения
- •Формы, виды и способы статистического исследования Формы статистического наблюдения
- •Виды статистического наблюдения
- •Виды статистического наблюдения по времени регистрации:
- •По полноте охвата единиц совокупности различают следующие виды статистического наблюдения:
- •Способы статистического наблюдения Способы получения статистической информации:
- •Ошибки статистического наблюдения
- •8.Современная организация государственной статистики России.
- •9.Статистическая отчётность.
- •10.Контроль материалов наблюдения.
- •11. Понятие, методы расчёта абсолютных и относительных величин.
- •12.Виды относительных величин.
- •13.Принципы построения относительных величин. Системы статистических показателей.
- •Система статистических показателей —
- •14.Графическое отображение статистических данных.
- •15.Понятие, сущность, значение средних величин.
- •16.Средняя арифметическая и её свойства.
- •17.Виды степенных средних.
- •18.Структурные средние величины.
- •19.Понятие и сущность рядов динамики в статистике
- •20. Показатели динамики
- •Примеры расчетов показателей динамики
- •Абсолютный прирост
- •Темп роста
- •Темп прироста
- •Абсолютное значение 1%-го прироста
- •21. Средние показатели рядов динамики Средний уровень ряда в статистике
- •Средний абсолютный прирост в задачах статистики
- •Средний темп роста
- •Средний темп прироста
- •22.Понятие и методология выравнивания рядов динамики. Приведение рядов динамики к одинаковому основанию
- •Методы выравнивания рядов динамики
- •Метод укрупнения интервалов времени (гр. 3).
- •Метод скользящей средней
- •23.Анализ сезонных колебаний
- •24.Аналитическое выравнивание Метод аналитического выравнивания
- •25.Методы прогнозирования в статистике
- •Тема 7. Статистические методы прогнозирования: экспоненциальное сглаживание и анализ временных рядов.
- •26.Показатели размера и интенсивности вариации
- •27.Показатели и формы распределения
- •28.Нормальное распределение и его свойства
- •29.Сущность, значение и категории выборочного наблюдения.
- •30. Виды и способы отбора.
- •31.Ошибки выборочного наблюдении
- •32.Определение объёма выборки.
- •33. Понятие корреляционно-регрессионного анализа в статистике.
- •34. Множественный корреляционно-регрессионный анализ.
- •35. Метод корреляционно-регрессионного анализа.
- •36.Понятие и основные элементы индексов.
- •37.Виды индексов.
- •38.Агрегатные индексы.
- •39.Индексный анализ при изучении экономических явлений.
- •Агрегатные индексы качественных показателей
- •Агрегатные индексы объемных показателей
- •Ряды агрегатных индексов с постоянными и переменными весами
- •Построение сводных территориальных индексов
- •Средние индексы
- •40.Средневзвешенные индексы.
17.Виды степенных средних.
редние величины делятся на два больших класса: степенные и структурные. К последним относятся мода и медиана, но наиболее часто применяются степенные различных видов.
Степенные средние, в зависимости от представления отдельных величин, могут быть простыми и взвешенными. Простая средняя рассчитывается при наличии двух и более статистических величин, расположенных в произвольном порядке. Общая формула простой средней величины имеет вид
![]() =
=![]() . (1.11)
. (1.11)
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы
= (1.12)
(1.12)
При этом обозначено:
Xi – значения отдельных статистических величин или середин группировочных интервалов;
m - показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая и так далее.
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида. Так, приняв m = 1, находим, что простая средняя арифметическая величина определяется по формуле
![]() =
=![]() . (1.13)
. (1.13)
Аналогично
для взвешенной средней арифметической
величины получаем формулу через частоты
или через доли (так как ![]() )
)
=![]() . (1.14)
. (1.14)
Не представляет трудностей и вывод формул для простых и взвешенных средних квадратических и кубических величин. Несколько сложнее вывод средней гармонической при m = –1. Так, используя формулу (1.11), имеем вначале
гм
=  =
= ![]() ,
,
а окончательно получим, что простая средняя гармоническая величина определяется по формуле
ГМ
= ![]() , (1.15)
, (1.15)
Аналогично выводится формула взвешенной средней гармонической величины, которая имеет следующий окончательный вид через частоты или через доли
ГМ
=  , (1.16)
, (1.16)
Наиболее часто употребляются формулы средних арифметических и гармонических величин.
18.Структурные средние величины.
роме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены ,в основном, модой и медианой.
Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
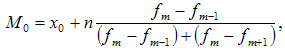
где:
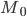 —
значение моды
—
значение моды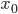 —
нижняя граница
модального интервала
—
нижняя граница
модального интервала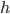 —
величина интервала
—
величина интервала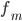 —
частота модального
интервала
—
частота модального
интервала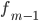 —
частота интервала,
предшествующего модальному
—
частота интервала,
предшествующего модальному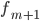 —
частота интервала,
следующего за модальным
—
частота интервала,
следующего за модальным
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для
определения медианы в
дискретном ряду при
наличии частот сначала вычисляют
полусумму частот ![]() ,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
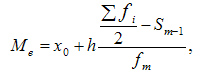
где:
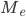 —
искомая медиана
—
искомая медиана— нижняя граница интервала, который содержит медиану
— величина интервала
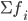 —
сумма частот или
число членов ряда
—
сумма частот или
число членов ряда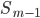 -
сумма накопленных частот интервалов,
предшествующих медианному
-
сумма накопленных частот интервалов,
предшествующих медианному— частота медианного интервала
Пример. Найти моду и медиану.
Возрастные группы |
Число студентов |
Сумма накопленных частот ΣS |
До 20 лет |
346 |
346 |
20 — 25 |
872 |
1218 |
25 — 30 |
1054 |
2272 |
30 — 35 |
781 |
3053 |
35 — 40 |
212 |
3265 |
40 — 45 |
121 |
3386 |
45 лет и более |
76 |
3462 |
Итого |
3462 |
|
Решение: В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
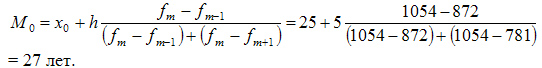
Это значит что модальный возраст студентов равен 27 годам.
Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
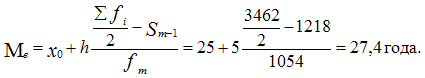
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100 частей.
