
- •Аналіз показників інтенсивності часових рядів
- •2. Визначення тенденцій розвитку та коливань соціально-економічних явищ і процесів
- •2.1 Згладжування часового ряду методом ковзної середньої
- •Статистичі методи вивчення взаємозв’язів явищ
- •Кореляційно-регресійний аналіз взаємозв’язку явищ
- •Індексний метод
- •4.1 Застосування індексного методу в статистичному аналізі соціально-економічних явищ і процесів
Статистичі методи вивчення взаємозв’язів явищ
Кореляційно-регресійний аналіз взаємозв’язку явищ
Задача 4. 11. За даними аудиторського висновку про діяльність комерційних банків, встановлено залежність між розміром кредитної ставки та дохідністю кредитних операцій:
Таблиця 3.1 - Дані аудиторського висновку про діяльність комерційних банків
Банк |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Кредитна ставка,% |
15,2 |
16,0 |
16,0 |
16,5 |
16,8 |
15,5 |
15,0 |
Дохідність кредитних операцій, % |
23,0 |
34,0 |
30 |
28 |
29 |
28 |
26 |
Визначити:
параметри лінійного рівняння регресії;
коефіцієнт еластичності;
коефіцієнт детермінації та індекс кореляції;
лінійний коефіцієнт кореляції Пірсона;
істотність зв’язку за допомогою F-критерію Фішера та t-критерію Стьюдента.
Зробити висновки.
Таблиця 3.2 – Проміжні розрахунки
Банки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Сума |
Серед значення |
Кредитна ставка,% x |
15,20 |
16,00 |
16,00 |
16,50 |
16,80 |
15,50 |
15,00 |
111,00 |
15,86 |
Дохідність кредитних операцій, % y |
23,00 |
34,00 |
30,00 |
28,00 |
29,00 |
28,00 |
26,00 |
198,00 |
28,29 |
x2 |
231,04 |
256,00 |
256,00 |
272,25 |
282,24 |
240,25 |
225,00 |
1762,78 |
251,83 |
y2 |
529,00 |
1156,00 |
900,00 |
784,00 |
841,00 |
784,00 |
676,00 |
5670,00 |
810,00 |
xy |
349,60 |
544,00 |
480,00 |
462,00 |
487,20 |
434,00 |
390,00 |
3146,80 |
449,54 |
Y |
-21451,04 |
-24620,83 |
-24620,83 |
-26743,00 |
-28069,59 |
-22607,63 |
-20701,06 |
-168813,98 |
-24116,28 |
(y-ȳ)2 |
27,94 |
32,65 |
2,94 |
0,08 |
0,51 |
0,08 |
5,22 |
69,43 |
х |
(Y-Ȳ)2 |
7103498,11 |
254566,71 |
254566,71 |
6899658,72 |
15628601,54 |
2276030,16 |
11663756,54 |
44080678,48 |
х |
(x-x̄̄)2 |
0,43 |
0,02 |
0,02 |
0,41 |
0,89 |
0,13 |
0,73 |
2,64 |
х |
(Y-y)2 |
461134585,78 |
607860610,63 |
607663387,99 |
716686626,11 |
789530530,95 |
512371815,44 |
429610978,23 |
4124858535,12 |
х |
(y-Y)2 |
461134585,78 |
607860610,63 |
607663387,99 |
716686626,11 |
789530530,95 |
512371815,44 |
429610978,23 |
4124858535,12 |
х |
Важливою
характеристикою кореляційного зв’язку
є лінія регресії ‑ емпірична в моделі
аналітичного групування і теоретична
в моделі регресійного аналізу. Емпірична
лінія регресії представлена груповими
середніми результативної ознаки
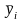 ,
кожна з яких належить до відповідного
інтервалу значень групувального фактора
хj.
Теоретична лінія регресії описується
певною функцією
,
кожна з яких належить до відповідного
інтервалу значень групувального фактора
хj.
Теоретична лінія регресії описується
певною функцією
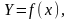 яку називають рівнянням регресії, а Y ‑
теоретичним рівнем результативної
ознаки.
яку називають рівнянням регресії, а Y ‑
теоретичним рівнем результативної
ознаки.
Якщо зі зміною фактора х результат у змінюється більш-менш рівномірно, такий зв’язок описується лінійною функцією Y = a + bx. Коли йдеться про нерівномірне співвідношення варіацій взаємозв’язаних ознак (наприклад, коли прирости значень у зі зміною х прискорені чи сповільнені або напрям зв’язку змінюється), застосовують нелінійні регресії, зокрема:
степеневу
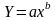 ;
;гіперболічну
 ;
;параболічну
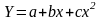 тощо.
тощо.
Рівняння регресії характеризує зміну середнього рівня результативної ознаки у залежно від зміни факторної ознаки х. Воно визначає математичне сподівання групових середніх результативної ознаки під впливом різних значень факторної ознаки.
У разі лінійної форми зв'язку результативна ознака змінюється під впливом факторної ознаки рівномірно:
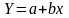 (3.1)
(3.1)
де
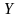 ‑ згладжене
середнє значення результативної ознаки;
‑ згладжене
середнє значення результативної ознаки;
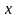 ‑ факторна
ознака;
‑ факторна
ознака;
a і b ‑ параметри рівняння;
а ‑ значення Y при x= 0;
b ‑ коефіцієнт регресії.
В рівнянні прямої параметр а економічного змісту немає.
Параметр b (коефіцієнт регресії) величина іменована, має розмірність результативної ознаки і розглядається як ефект впливу x на y. Параметр a ‑ вільний член рівняння регресії, це значення y при x = 0. Якщо межі варіації x не містять нуля, то цей параметр має лише розрахункове значення.
Коефіцієнт регресії b вказує на те, наскільки змінюється результативна ознака Y внаслідок зміни факторної ознаки x на одиницю.
Якщо b має позитивний знак, то зв'язок прямий, якщо від'ємний ‑ зв'язок обернений.
Параметри рівняння зв'язку визначають шляхом розв’язання системи нормальних рівнянь за методом найменших квадратів, основною умовою якого є мінімізація суми квадратів відхилень емпіричних значень від теоретичних:
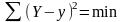 (3.2)
(3.2)
Система нормальних рівнянь для визначення параметрів парної лінійної регресії має вигляд:
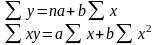 (3.3)
(3.3)
де n ‑ число членів у кожному з двох порівнюваних рядів;
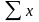 ‑ сума
значень факторної ознаки;
‑ сума
значень факторної ознаки;
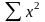 ‑ сума
квадратів значень факторної ознаки;
‑ сума
квадратів значень факторної ознаки;
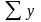 ‑ сума
значень результативної ознаки;
‑ сума
значень результативної ознаки;
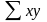 ‑ сума
добутків значень факторної та
результативної ознаки.
‑ сума
добутків значень факторної та
результативної ознаки.
‑ теоретичні значення результативної ознаки
Розв'язавши дану систему рівнянь, одержують формули розрахунків параметрів парного лінійного рівняння регресії:
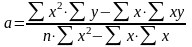 (3.4)
(3.4)
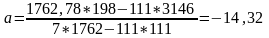
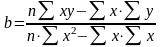 (3.5)
(3.5)
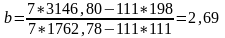
На основі рівняня регресії визначаються теоретичні значення Y, тобто значення результативної ознаки за умови впливу лише фактора х при незмінному рівні інших факторів.
Досить часто ознаки, що досліджуються, мають різні одиниці вимірювання, тому для оцінки впливу факторної ознаки на результативну використовують характеристику відносної зміни у за рахунок х , яка називається коефіцієнтом еластичності.
Він показує, на скільки відсотків в середньому змінюється результативна ознака у при зміні факторної ознаки х на 1,0%. Відповідно, для лінійної залежності коефіцієнт еластичності визначається за формулою:
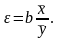 (3.6)
(3.6)
Коефіцієнт еластичності в нашому випадку буде рівним:
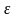
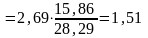
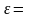 1,51,
що означає: зі зміною факторної ознаки
на 1% результативна змінюється на 151%.
1,51,
що означає: зі зміною факторної ознаки
на 1% результативна змінюється на 151%.
Відхилення фактичних значень у від теоретичних Y називаються залишковими. Вони характеризують вплив на результативну ознаку всіх інших факторів, окрім х. Середній розмір цих відхилень визначає залишкова дисперсія:
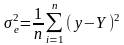 (3.7)
(3.7)
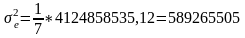
Варіацію у, зумовлену впливом тільки фактора х вимірює факторна дисперсія:
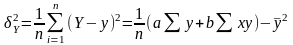 (3.8)
(3.8)
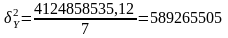
Загальна дисперсія дорівнює:
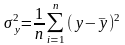 (3.9)
(3.9)
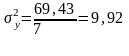
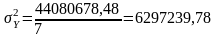
Частка факторної дисперсії у загальній характеризує щільність зв’язку і називається коефіцієнтом детермінації:
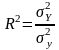 (3.10)
(3.10)
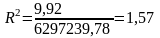
Отже частка факторної дисперсії у загальній становить 1,57%.
Щільність зв’язку оцінюється також індексом кореляції:, який є коренем квадратним з коефіцієнта детермінації, якщо зв'язок лінійний.
Звідси:
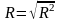 (3.11)
(3.11)
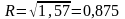
Індекс кореляції оцінює щільність зв'язку. Він, як і емпіричне кореляційне відношення, вимірює лише щільність зв'язку і не вказує на її напрямок. Отже зв'язок є щільним.
Для доповнення дослідження напрямку зв'язку у разі лінійної залежності використовують лінійний коефіцієнт кореляції (Пірсона):
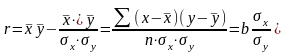 (3.12)
(3.12)
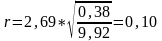
Лінійний коефіцієнт кореляції r коливається в межах від –1 до +1, і тому характеризує не тільки щільність, а й напрямок зв’язку. Додатне значення свідчить про прямий зв'язок між ознаками, а від'ємне – про зворотний.
В даному випадку зв’зок між ознаками прямий.
Таблиця 3.3 ‑ Градація щільності зв'язку
Зв'язок |
Лінійний коефіцієнт кореляції |
|
Прямий зв'язок |
Зворотний зв'язок |
|
Слабкий Середній Щільний |
0,100...0,300 0,300…0,700 0,700...0,990 |
‑0,100...‑0,300 ‑0,300...‑0,700 ‑0,700...‑0,990 |
Отже за даними таблиці зробимо висновок про високу щільність зв’язку між факторною та результативною ознакою.
Перевірка
істотності зв’язку здійснюється таким
же чином, як і в моделі аналітичного
групування, шляхом порівняння
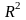 та
.
та
.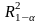 .
.
Ступені вільності залежать від числа m параметрів рівняння регресії k1=m ‑ 1 і кількості одиниць n досліджуваної сукупності k2=n-m.
Істотність
зв'язку перевіряють за допомогою
F-критерію Фішера, який функціонально
пов'язаний з
та
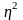 .
.
Фактичне значення F критерію визначають за формулою:
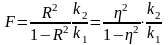 (3.13)
(3.13)
F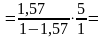 -12,
-12,
F tab(1;5)=230,2.
-12 <230,2
Якщо
ж
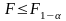 ‑ різниця
між дисперсіями зумовлена впливом
випадкових факторів.
‑ різниця
між дисперсіями зумовлена впливом
випадкових факторів.
Для встановлення достовірності обчисленого лінійного коефіцієнта кореляції використовують критерій Стьюдента (t ‑ критерій):
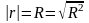 (3.14)
(3.14)
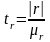 (3.15)
(3.15)
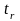
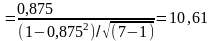 2
2
де
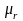 ‑ середня
похибка коефіцієнта кореляції, яку
визначають за формулою:
‑ середня
похибка коефіцієнта кореляції, яку
визначають за формулою:
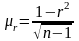 (3.16)
(3.16)
