2.4 Колебания в кристаллах

Кристалл представляет собой совокупность атомов, связанных упругими силами. В зависимости от расположения атомов кристаллическая решетка может быть простой, гранецентрированной, объёмно-центрированной и т.д. При малых амплитудах смещения атомов из их положения равновесия  справедливо гармоническое приближение описания колебаний. Под действием теплового возбуждения атомы в кристалле находятся в непрерывном движении.

Рисунок 2- колебания атомов в одномерном кристалле

Рассмотрим колебания атомов в одномерном кристалле. Представим такой кристалл в виде цепочки шариков с массами m₁ и m₂, соединенных пружинами с жесткостью c. Сила, действующая на каждый шарик, зависит от относительного смещения двух других шариков, лежащих справа и слева от рассматриваемого. Поэтому, смещение каждого шарика u_n и u_m (см. рисунок) задается следующей системой уравнений:

m₁(d²u_n/dt²) = -c(2u_n - u_m-1 - u_m) m₂(d²u_m/dt²) = -c(2u_m - u_n - u_n+1) (1)

Эти уравнения описывают колебательное движение атомов в одномерном кристалле:

u_n = A₁exp{ i(kan-wt) } u_m= A₂exp{ i(kam-wt) }

где a/2 - расстояние между ближайшими атомами, k=2p/l - волновое число, l - длина волны в кристалле. Уравнения, приведенные выше, имеют два решения относительно w:

w₁² = (w₀²/2) [ 1 - (1-g²sin²(ak/2))^1/2 ] w₂²= (w₀²/2) [ 1 + (1-g²sin²(ak/2))^1/2 ]

где g² = 4m₁m₂/(m₁+m₂)²_; w₀² = 2c (m₁+m₂)/m₁m₂. Эти уравнения определяют две ветви дисперсионной кривой (так называемая акустическая ветвь и оптическая ветвь).

3.Сингонии

Классификационное подразделение кристаллов по признаку симметрии элементарной ячейки кристалла, характеризуется соотношениями между её рёбрами и углами. Существует 7 сингоний: кубическая, гексагональная, тетрагональная, тригональная, ромбическая, моноклинная, триклинная.

Трехмерная система координат в анизотропной кристаллической среде выбирается в соответствии с симметрией среды[5]

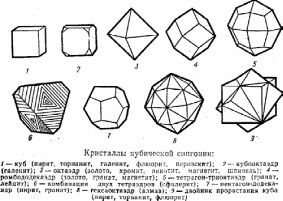
 Рисунок 3- кристаллы кубической сингонии

4.Индексы кристаллографических граней

Индексы кристаллографических граней - три целых числа, определяющие расположение в пространстве граней и атомных плоскостей кристалла (индексы Миллера), а также направлений в кристалле и его рёбер (индексы Вейса) относительно кристаллографии осей. Прямая и параллельное ей ребро, определяемые индексами Вейса р1, р2, р3 (обозначаются [p1p2p3]), проходят из начала координат О в точку А, определяемую вектором p1a+p2b+p3c, где а, b, с - периоды решётки (на рис. прямая ОА определяется индексами Вейса. Кристаллография плоскость отсекает на осях координат, построенных на векторах a., b, c, отрезки р1а, p'2b, р'3с (p'1, р'2, р'3 - целые числа); щелочил обратные отношения 1/p'1 : 1/p'2 : 1/p'3=h:k:l определяют индексы Миллера (hkl)данной плоскости. Напр., для плоскостей Р на рис. p'1=2, p'2=3, р'3=6; обратные отношения этих величин 1/2:1/3:1/6 можно привести к целым числам: 6/2 : 6/з : 6/6=3:2:1, т. е. плоскость Р определяется миллеровскими индексами[6]

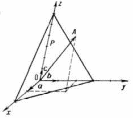
Прямая ОА с индексами Вейсаи плоскость Р с индексами Миллера ; Ох, Оу, Оz - кристаллографические оси

Рисунок 4