6. Режимы работы линии без потерь

6.1. Режим бегущих волн

Если линия нагружена на активное сопротивление, равное волновому, т.е. Z_н=ρ, то, как следует из (22), коэффициент отражения р=0, а из определения (21) получаем, что (и =0), а, следовательно, и =0. Таким образом, при Z_н=ρ в линии существуют только падающие волны и она становится эквивалентной полубесконечной линии без потерь. Поэтому нагрузка Z_н=ρ называется согласованной, а соответствующий режим в линии – режимом бегущих волн. В этом режиме в линии происходит идеальная канализация высокочастотной энергии, которая полностью поглощается нагрузкой. Для режима бегущих волн ( =0) уравнения (13а) и (13б) принимают вид:

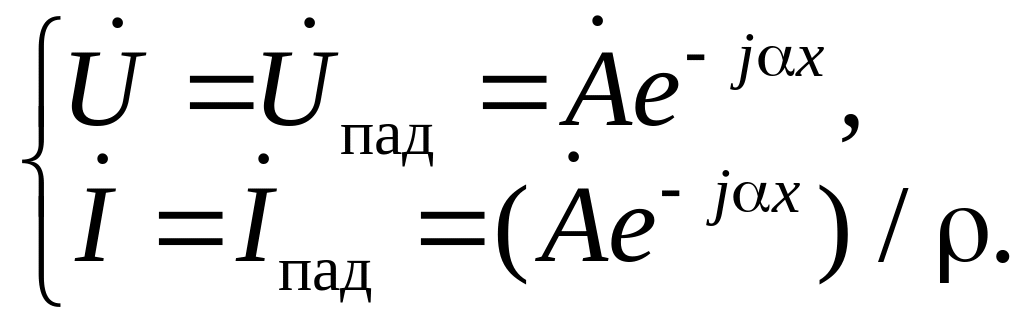
Но учитывая, что , из первого уравнения (16) получаем:

,

где U_н – действительная амплитуда напряжения на нагрузке, ψ – некоторая его начальная фаза. Для простоты, не искажающей существа процесса, можно положить ψ=−αl, так что =U_н, и тогда

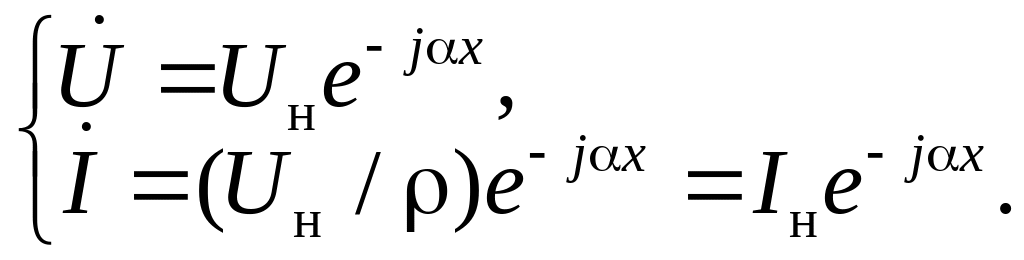
Следовательно, для мгновенных значений напряжения и тока в линии получаем:

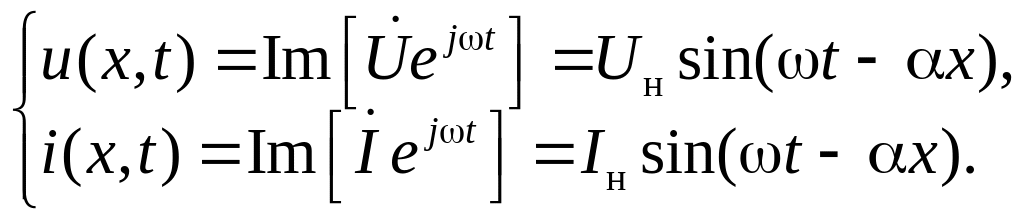
Эти функции и представляют бегущие синусоидальные волны напряжений и токов в линии. Из них видно, что в режиме бегущих волн:

● амплитуды напряжения и тока постоянны на всей линии:

U=const=U_н, I=const=I_н;

● напряжение и ток в каждом сечении линии изменяются синфазно, т.е. сдвиг фаз между ними φ=0; а это означает, что вдоль линии от генератора к нагрузке переносится активная мощность

P= ,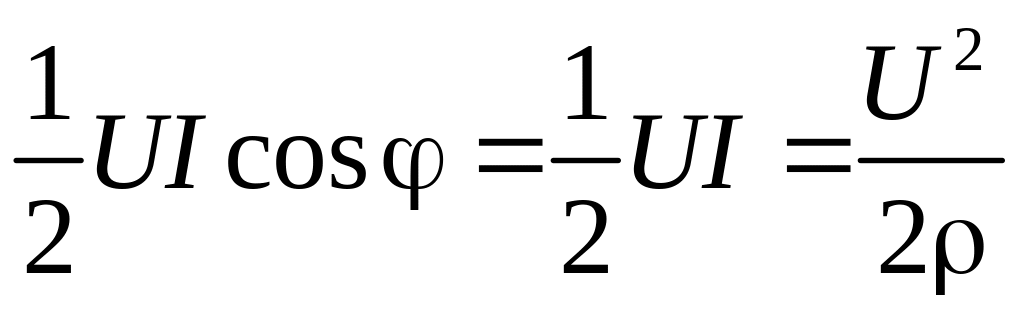

которая вся и поглощается нагрузкой.

Н о высокочастотные напряжения и токи создают вокруг проводов переменные электрическое и магнитное поля, ориентированные в плоскости поперечного сечения линии, как показано на рис. 5. Следовательно, вдоль линии бегут волны электрического и магнитного полей − электромагнитные волны. Можно показать. что энергия от генератора к нагрузке переносится именно этими волнами, а провода линии лишь задают направление переноса. Плотность потока электромагнитной энергии характеризуется вектором Пойнтинга

П=Е×Н= (Е×В),

который в данном случае постоянен по величине и направлен вдоль линии от генератора к нагрузке.

Так как поля Е и В в двухпроводной линии имеют только поперечные компоненты, а фронт электромагнитной волны (т.е. поверхность постоянной фазы волны) является плоским, то такие волны называются плоскими поперечными волнами типа ТЕМ (Transverse Electric-Magnetic).

Как следует из (20), в режиме бегущих волн (т.е. при Z_н=ρ) входное сопротивление в любом сечении линии Z_вх=ρ, т.е. постоянно и чисто активно.

6.2. Режим стоячих волн

Если амплитуды падающих и отражённых волн равны, то говорят, что линия работает в режиме стоячих волн. В этом режиме, как следует из (21), р=1.

Из формул (22) и (23) видно, что режим стоячих волн в линии реализуется в следующих трёх случаях:

● Z_н=∞ (линия на конце разомкнута);

● Z_н=0 (короткозамкнутая линия);

● Z_н=jX_н (линия, нагруженная на реактивное сопротивление).

Ограничимся анализом процессов в линии в первых двух вариантах.

6.2.1. Разомкнутая линия (Z_н=∞)

При Z_н=∞ ток , следовательно, уравнения (17) примут вид:

, ;

и для мгновенных значений напряжения и тока в линии получаем:

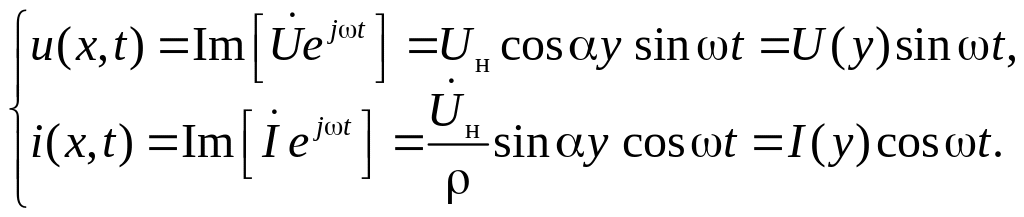
Эти соотношения описывают стоячие волны в линии, которые характеризуются следующими свойствами:

1. Амплитуды напряжения и тока в линии зависят от координаты у:

, . (25)

Максимальные значения амплитуды напряжения (U_max=U_н) называются пучностями напряжения, а минимальные (U_min=0) –узлами напряжения. Видно, что координаты пучностей напряжения определяются из условия

cos αy=±1, т.е. αу=πk (k=0, 1, 2, …),

а координаты узлов напряжения – из условия

cos αy=0, т.е. αу=π(k+1/2) (k=0, 1, 2, …).

Тогда, учитывая. что α=2π/λ (соотношение (24)), получаем для координат пучностей и узлов напряжения:

,

А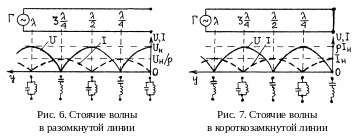 налогично определяются положения пучностей и узлов тока; при этом получается, что узлы тока совпадают с пучностями напряжения и наоборот (рис.6).

2. Фаза колебаний напряжения между узлами не зависит от у, а при переходе через узел скачком меняется на π. Аналогично для фазы тока.

3. В каждом сечении линии разность фаз между мгновенными значениями тока и напряжения φ=π/2, следовательно, активная мощность по линии не переносится ( ); энергия лишь на локальных участках превращается из электрической в магнитную и наоборот.

Как видно из (20), входное сопротивление разомкнутой линии

Z_вх= .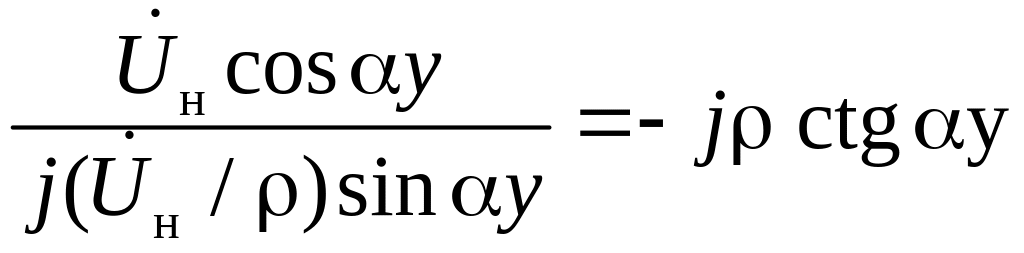

При αу=πk, т.е. при у=k (k=0, 1, 2, …), т.е. в узлах тока, Z_вх=∞, как у параллельного контура; а при у= +πk=(2k+1) (k=0, 1, 2, …), т.е. в узлах напряжения, Z_вх=0, как у последовательного колебательного контура.

Определение. Отрезки линии у=k (k=1, 2, …), ведущие себя как параллельный или последовательный контуры, называются резонансными.

Резонансные отрезки имеют одно важное свойство: из формулы (20) следует, что при любой нагрузке Z_н входное сопротивление четвертьволновых отрезков (k=1, 3, 5, …)

Z_вх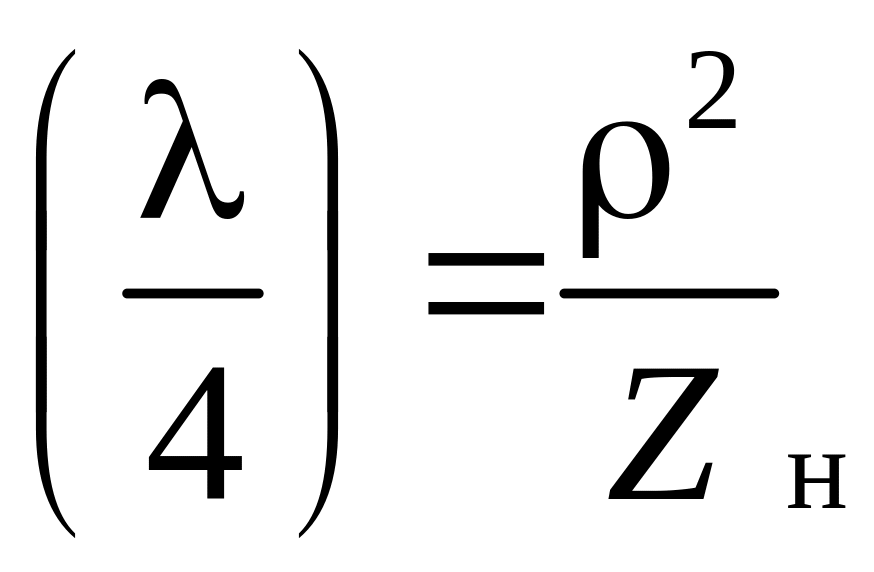 , (26а)

а входное сопротивление полуволновых отрезков (k=2, 4, 6, …)

Z_вх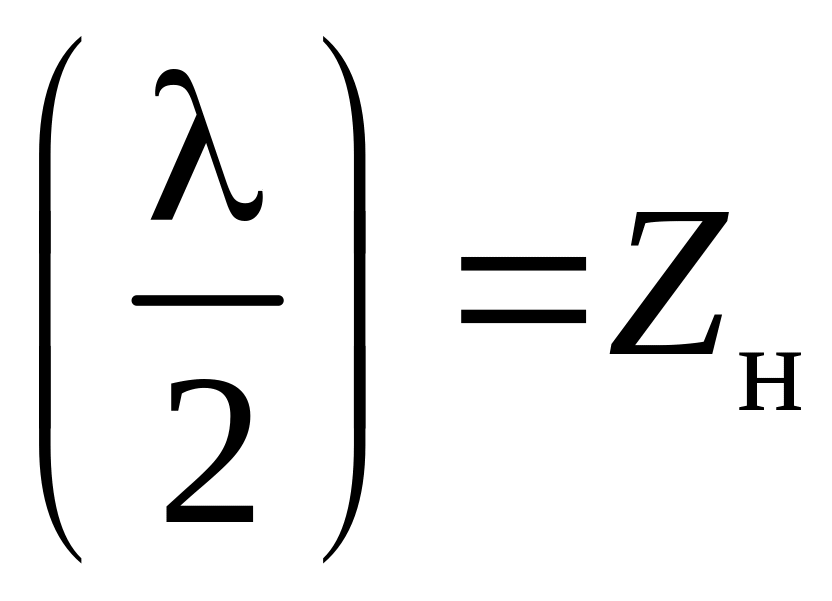 . (26б)

Последнее означает, что полуволновый отрезок линии с нагрузкой Z_н эквивалентен самой нагрузке Z_н.

6.2.2. Короткозамкнутая линия (Z_н=0)

При Z_н=0 напряжение на конце линии , следовательно, уравнения (17) принимают вид:

, ;

и для мгновенных значений напряжения и тока получаем:

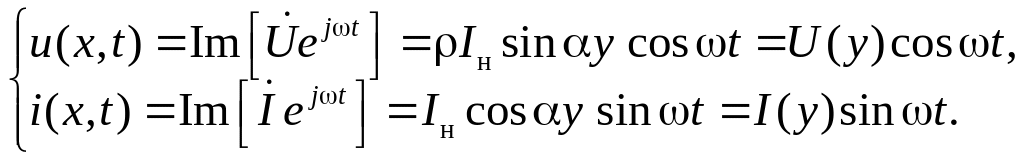
Эти соотношения, как и в предыдущем случае Z_н=∞, описывают стоячие волны, только здесь координаты пучностей и узлов напряжения будут:

, ,

т.е. взаимно меняются по сравнению с вариантом Z_н=∞. То же самое для пучн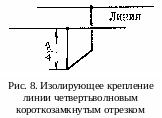 остей и узлов тока (рис. 7).

Замечание. Из формулы (26а) следует, что входное сопротивление четвертьволнового короткозамкнутого отрезка ∞. Это свойство позволяет применять такие отрезки в качестве изолирующих креплений линии (рис. 8), так как они не шунтируют линию ни в каком месте и не нарушают режим её работы.