4. Решение телеграфных уравнений для линии без потерь

при установившемся синусоидальном процессе

Пусть выходное напряжение генератора является синусоидальным с частотой ω. При подключении к нему линии в ней начнётся переходный процесс, длительность которого зависит от длины линии и потерь в ней. Реально он заканчивается за время порядка 10⁻⁶ с, и в линии устанавливается стационарный волновой режим, который и будем рассматривать в дальнейшем. При этом режиме напряжение и ток в каждом сечении линии будут меняться по синусоидальному закону с частотой генератора ω, а их амплитуды и фазы зависеть от координаты х. В связи с этим, решение телеграфных уравнений (5а) и (5б) удобно искать в комплексном виде:

u(x,t)→ (х) , i(x,t)→ (х) , (9)

где (х)= − комплексная амплитуда (комплекс) напряжения,

(х)= − комплексная амплитуда (комплекс) тока,

U(x) и I(x) – действительные амплитуды напряжения и тока,

φ(х) и ψ(х) – начальные фазы напряжения и тока.

Комплексная запись решения (9) используется для удобства вычислений. Она даёт возможность перейти от уравнений в частных производных (5а) и (5б) к обыкновенным дифференциальным уравнениям относительно комплексов и . А чтобы вернуться к обычной (временнóй) форме записи мгновенных значений, надо после определения неизвестных величин (х) и (х) взять их реальные или мнимые части, например,

и(x,t)=Im Im .

Итак, подставим искомые функции вида (9) в уравнения (5а) и (5б). Получим систему обыкновенных дифференциальных уравнений для комплексов (х) и (х):

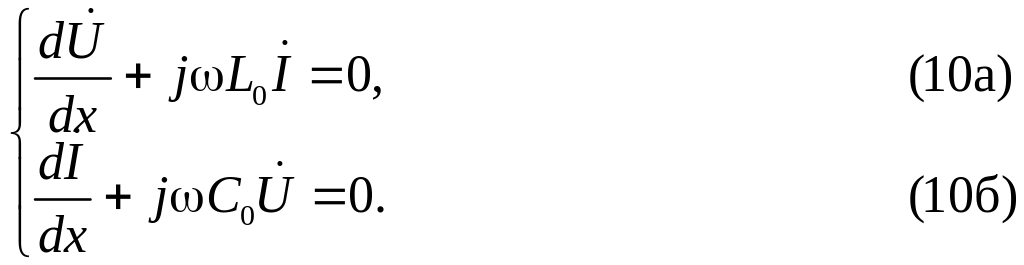
Подставляя теперь из (10а) в (10б), получим одно уравнение второго порядка для комплекса :

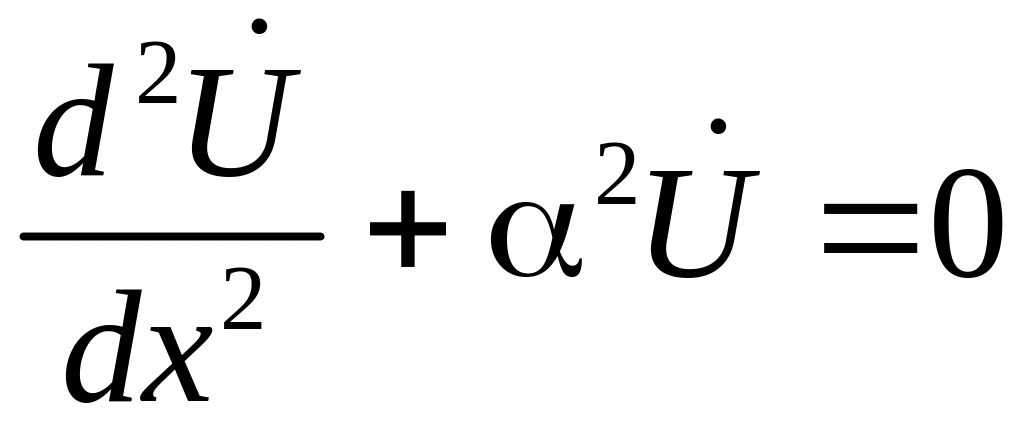, (11)

где

. (12)

Общее решение уравнения (11) имеет вид

, (13а)

где и − неопределённые пока комплексные коэффициенты.

Чтобы найти , теперь достаточно подставить выражение из (13а) в (10а); с учётом (12) это даёт:

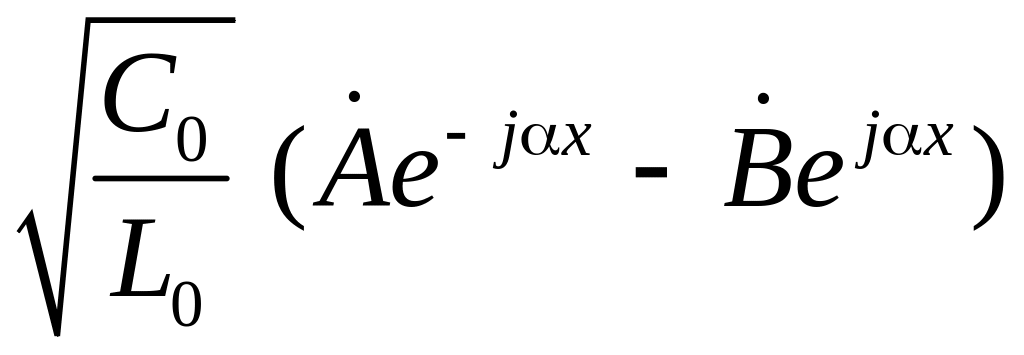= . (13б)

Первые слагаемые в (13а) и (13б) – это комплексные амплитуды напряжения и тока прямой волны, а вторые – обратной. Действительно, например, первое слагаемое (13а) соответствует волне

, (14)

где U_пр – амплитуда прямой волны. Здесь U_пр и есть тот конкретный вид функции из (8), представляющей прямую волну общего вида.

Важнейшим параметром линии является её волновое сопротивление.

Определение. Отношение комплексных амплитуд напряжения и тока в прямой (или в обратной) волне называется волновым сопротивлением линии (ρ). Таким образом, из (13а) и (13б), по определению, имеем:

ρ=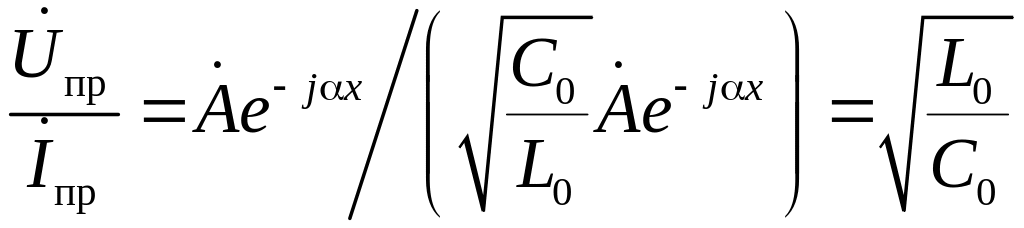 [Ом]. (15)

Коэффициенты и в (13а) и (13б) определяются из граничных условий, а именно – по измеряемым току и напряжению на нагрузке в конце линии. Пусть в конце линии, в сечении х=l установлена нагрузка, имеющая комплексное сопротивление Z_н, а напряжение и ток на ней равны

и (рис. 4). Тогда для х=l уравнения (13а) и (13б) примут вид:

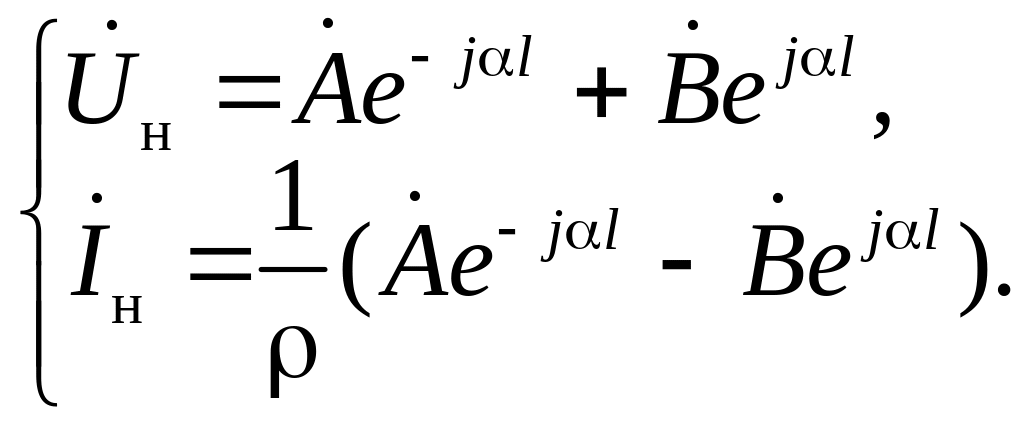
Складывая и вычитая эти уравнения, получаем:

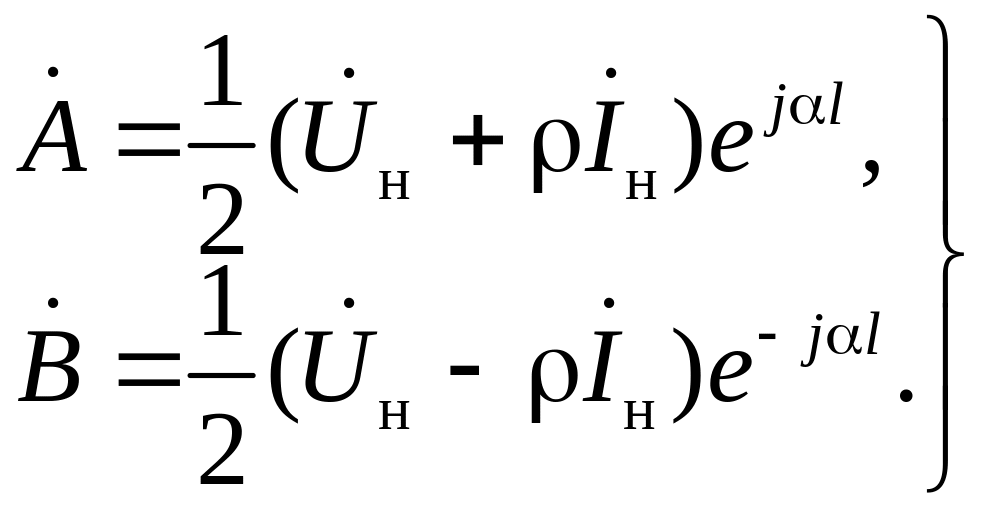(16)

Теперь (13а) и (13б) с подстановкой в них (16) принимают вид:

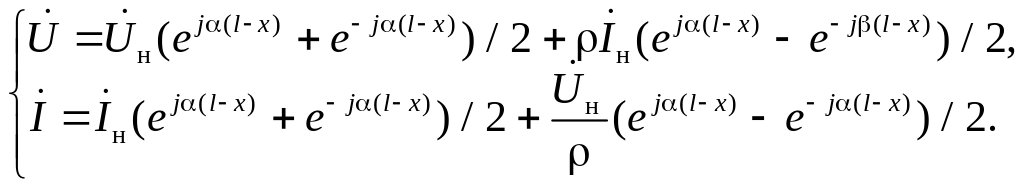
Из этих уравнений видно, что координату удобнее отсчитывать от нагрузки влево, т.е. положить у=l−х, как показано на рис. 4. И тогда, учитывая, что

окончательно получаем для комплексных амплитуд напряжения и тока в линии:

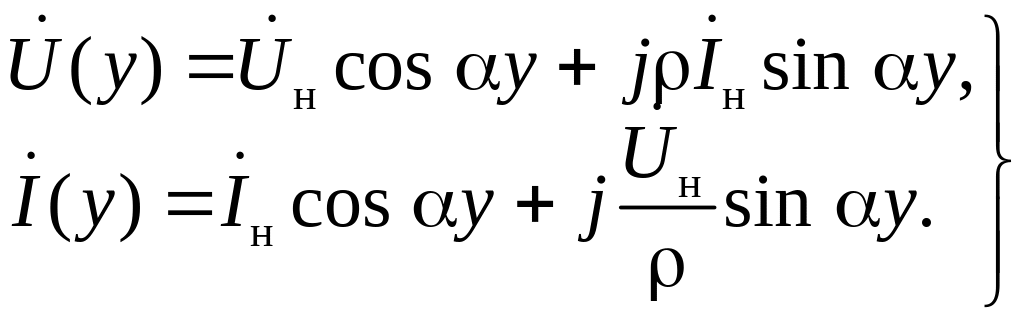(17)

Комплексные амплитуды и определяются мощностью генератора. Кроме того, они связаны законом Ома: =Z_н .