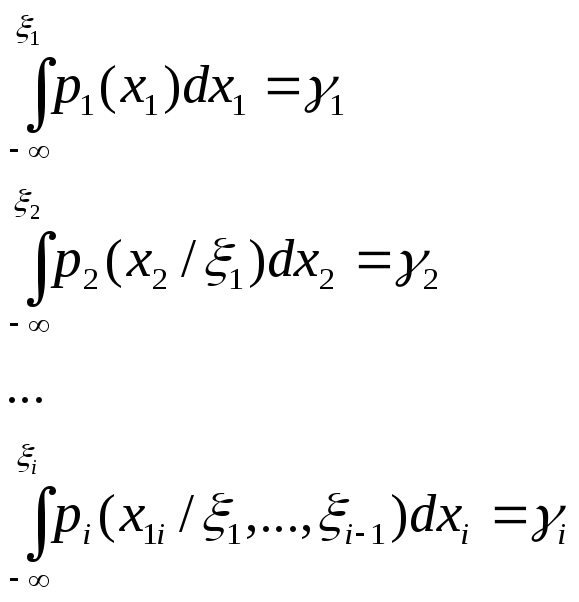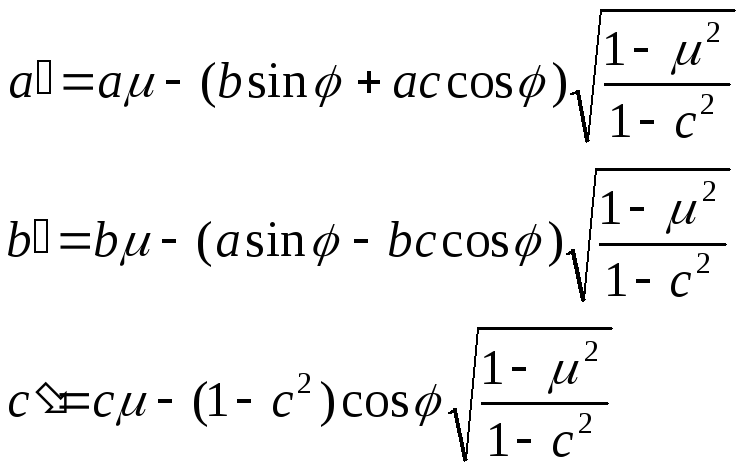11. Моделирование нормального распределения

Промоделируем нормальное распределение.

Пусть есть 2 случайные величины, распределенные по нормальному закону: . Промоделировать их сложно, так как сложно вычислить интеграл.

Эти величины не зависимы .

Перейдем к полярным координатам: иможно увидеть что:, гдеи- равномерно распределена – эти величины тоже независимы и. Теперь можно промоделировать величиныипо известной формуле.

Специальные методы.

Нормальное распределение: Например: - применять для «хвостов нельзя»

Можно уменьшить :

Показательное распределение:,

расположим по возрастанию: слева -, справа -.- подчиняется плотности.

Пример:

12. Моделирование обобщенного показательного распределения

Может возникать ситуация когда сечение зависит от координат, аf(x) – эта зависимость. В случае отсутствия этой зависимости распределение превратится в.

Пусть есть случайная величина с плотностью, имеющей вид показательного распределения :

. Пусть а – верхняя граница функцииf(x) - . - частица взаимодействует – это условие необходимо, потому что компьютер должен выдать хоть один ответ, иначе он зациклится.

Берем для моделирования другое :	На каждом шаге моделируем , из распределения, и вычисляем, прибавляя к нему каждый раз добавочку (то что в скобках) и проверяем выполнение условия:		При выполненном условии
		- 2 возможных случая.

13. Общий метод моделирования многомерных распределений

Пусть у нас есть измерений.

Пусть ,.

Получаем два случая:

1. попроще. Случайные координаты независимы. - получаем- одномерных задач, которые решаются как обычные одномерные задачи.

2. посложнее. .

Вычислим их следующим образом: .

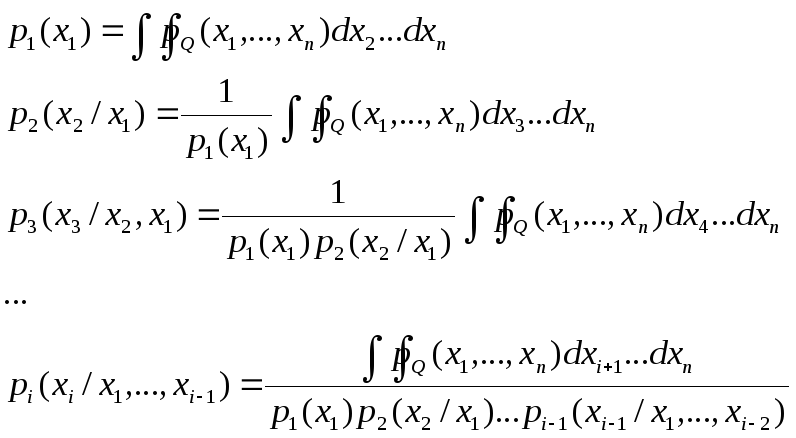Изменяя порядок рассмотрения можно получить разные системы каждая из которых приведет к решению задачи. Всего можно составить вариантов систем.

14. Метод исключения для многих переменных

Для многомерных задач можно применять любой метод, что и для одномерных, если представить исходную сумму в виде некой суммы по i.. Где- вероятности,;- плотности,. С помощью одной случайной величины повыбираем номерi(ту плотность что будем моделировать), потом моделируем плотность.

Метод исключения требует увеличения числа измерений на 1. , подбираем мажорирующую функцию. Моделируем точку, причем у – координата не зависимая от. После того как получили значения по координатам:- случайная точка.в (n+1)-мерном пространстве. Теперь надо проверить условие попадает ли точка в пространство, ограниченноg:. Если условие не выполняется, то надо снова получать новую точку в (n+1)-мерном пространстве.

Функция g₁должна удовлетворять тем же условиям что и мажорирующая функция в одномерном случае:

1.

2. - легко моделировать в смысле того, что должен получаться простой и быстрый алгоритм.

3. Не слишком много точек должно быть выкинуто, т.е. чтобы быстрее получались нужные точки должна быть близка к-близка к 1, где

15. Замена переменных в многомерном пространстве. Выбор случайного направления в 3-х мерном пространстве.

Замена переменных.

Если есть сделаем замену переменных- отображение одного пространства в другом (если это отображение взаимнооднозначно и дифференцируемо)..

Обратное , тогда.

Равномерно в шаре ,.,,,,.

Моделирование случайного направления.

,,.

- энергия частицы дол и после взаимодействия. - точка в которой находится частица. - направление движения частицы до и после взаимодействия. - косинус угла рассеяния. - индикатриса рассеяния. - макроскопическое сечение (обратное длины). ,- скалярное произведение. - случайная величина равномерно распределенная от 0 до.