
- •Способы получения стандартных случайных чисел. Представление случайных чисел в эвм. Период и отрезок апериодичности датчика случайных чисел.
- •Общий метод моделирования дискретных случайных величин.
- •Модификация метода моделирования дискретных случайных величин с повышенной эффективностью.
- •Общий метод моделирования непрерывных случайных величин.
- •Моделирование кусочно-постоянных непрерывных случайных величин.
- •Метод суперпозиции для дискретного параметра
- •Модифицированный метод суперпозиции с использованием одного случайного числа
- •Метод суперпозиции для непрерывного параметра
- •Метод исключения. Оптимизация.
- •Замена переменных. Использование полярных координат.
- •Моделирование нормального распределения
- •Моделирование обобщенного показательного распределения
- •Общий метод моделирования многомерных распределений
- •Метод исключения для многих переменных
- •Замена переменных в многомерном пространстве. Выбор случайного направления в 3-х мерном пространстве.
- •Общая схема моделирования процесса переноса
- •Моделирование длины свободного пробега в кусочно-однородной среде
- •Метод максимального сечения
- •Моделирование процесса размножения
Моделирование кусочно-постоянных непрерывных случайных величин.
Рассмотрим плотность распределения
величины
![]() :
:
![]() .
Промоделируем ее. Для этого разбиваем
ось х на отрезки до хn,
каждому из которых соответствует своя
плотностьy0…yn.
Проверяем равенство единице:
.
Промоделируем ее. Для этого разбиваем
ось х на отрезки до хn,
каждому из которых соответствует своя
плотностьy0…yn.
Проверяем равенство единице:![]() .
.
Пусть
![]() - это кусочек площади до
- это кусочек площади до![]() -
-![]() .
Решаем:
.
Решаем:![]() ,
т.е.
,
т.е.![]()
|
|
Последовательно вычитаем из М:
| |
|
|
Более точной способ, но более сложный.
Аналогично: последовательно вычитаем
из М:
Убираем
излишек площади «-М»:
| |
Существуют приемы, которые позволяют в некоторых случаях упростить общие методы – метод суперпозиции.
Метод суперпозиции для дискретного параметра
Метод суперпозиции основан на условных
вероятностях. Условная вероятность
![]() - вероятность наступления события А,
если наступило известное событие В.
- вероятность наступления события А,
если наступило известное событие В.
Условие
![]() - случайная величина с известным
распределением
- случайная величина с известным
распределением![]() .
Тогда плотность
.
Тогда плотность![]() представим в виде:
представим в виде:![]() ,
если
,
если![]() - дискретная случайная величина, тогда
- дискретная случайная величина, тогда![]() .
.
Рассмотрим как более простой случай метод суперпозиции для дискретного параметра.
Пусть
![]() ,
тогда
,
тогда![]()
Шаг 1: моделируем значение параметра
(номер параметра). Моделируем![]() по
по![]() ,
,![]() .
.
Шаг 2: моделируем условную плотность
для полученного параметра. Моделируем![]() по
по![]() .
.
Для того чтобы промоделировать этим
методом надо взять случайную величину
![]() ,
которое будет использоваться для первого
шага, и
,
которое будет использоваться для первого
шага, и![]() - для второго шага.
- для второго шага.

Фактически у нас фигурирует номер, а не само значение параметра.
Надо проверить выполняется ли
 ,
после чего можно применять метод
суперпозиции.
,
после чего можно применять метод
суперпозиции.
Пример: промоделируем следующую величину
![]() ,
где
,
где![]() - это значит что в остальных точках
- это значит что в остальных точках![]() .
.
![]() .
Чтобы не решать уравнение пятой степени,
решим эту задачу методом суперпозиции.
Для этого выделим величины
.
Чтобы не решать уравнение пятой степени,
решим эту задачу методом суперпозиции.
Для этого выделим величины![]() и
и![]() .
Необходимо подобрать константы так
чтобы интеграл был равен 1:
.
Необходимо подобрать константы так
чтобы интеграл был равен 1: .
.
Подставим:
![]() сравниваем это выражение с исходным.
Получим следующий результат:
сравниваем это выражение с исходным.
Получим следующий результат: ,
где
,
где![]() .
.
Для
![]() и
и![]() выполняются необходимые условия.
выполняются необходимые условия.
Теперь можно определить вид функций и записать ответ:

|
Если
|
|
Модифицированный метод суперпозиции с использованием одного случайного числа
Пусть
![]() ,
где
,
где![]() .
С помощью
.
С помощью![]() определить номер к (номер интервала в
который попадет
определить номер к (номер интервала в
который попадет![]() и будет номер к):
и будет номер к):![]() .
Вычислим
.
Вычислим![]() следующим способом:
следующим способом: ,
она будет равномерно распределена от
0 до 1. Тогда вычислим
,
она будет равномерно распределена от
0 до 1. Тогда вычислим![]() по известной формуле:
по известной формуле:![]() ,
при к=1 считать
,
при к=1 считать![]() .
.
Т.е сначала при помощи
![]() смоделировали номер к, а потом с помощью
смоделировали номер к, а потом с помощью![]() и этого номера к смоделировали саму
величину
и этого номера к смоделировали саму
величину![]() .
.
Плюсом этого метода является то что используется только одно случайное число, а минусом ухудшение качества.
Вспомним пример:![]() ,
в этом примере к определяется следующим
способом:
,
в этом примере к определяется следующим
способом: ,
тогда ξ:
,
тогда ξ: .
.
|
Если
|
|
 .
.![]()
![]()
Сначала мы моделируем номер – то есть выбираем, которую из функций будем моделировать, а потом моделируем саму эту функцию. В результате получится, что чаще всего мы будем моделировать простую функцию, а сложную значительно реже.



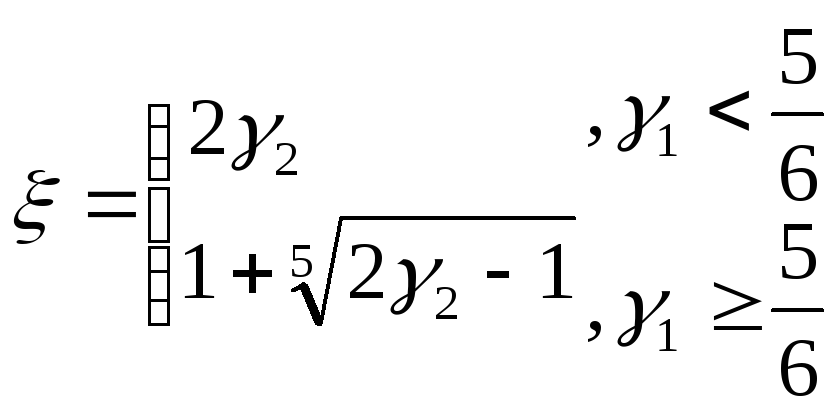 решение методом суперпозиции.
решение методом суперпозиции.