Лекция 11. Выборка

Пусть треб-ся изучить совок-ть однородных объектов отн-но некоторого качест-го или колич-го признака, харак-щего эти объекты.

Для изучен. некоторого признака совок-ти обьектов примен-т 2 вида обслед-ний:

1. Сплошное- изуч-ся все обьекты совок-ти. и 2. Выборочное (выборный метод)- изуч-ся часть обьекта совок-ти, а выводы распростр-ся на всю совок-ть обьектов.

Опр1. Генеральной совокупностью назыв. совок-ть всех однород-х обьектов, подлежащих изучению.

Замечание!!!Часто под генер-ной совок-тью поним-т иследованую СВ.

Опр2. Выборочной совокупностью или выборкой назыв. совок-ть обьектов, случайно отобраных из генер-ной совок-ти.

Опр3. Обьектом совок-ти(генер-ной или выборочной)назыв. число ее обьектов.

Типы выборок.

1. Повторная - отобраный обьект возвращается.

2. Безповторная - отобрн. обьект не возвращается.

Опр4. Выборка назыв. репрезентативной ( представленной), если она достаточно хорошо воспроизводит генер-ную совок-ть.

Опр5. Различные значения признака (СВ Х) назыв. вариантами и обознач. -х, а последовательтность вариант, записаных в возраст-м порядке назыв. вариантционным рядом.

Пусть выборка объема n содержит k различ. знач. ( вариант): х1, х2,...,хk.

Причем знач. х1 повторяется в выборке n1 раз, х2-n2,....xk-nk раз.

Опр6. Число Ni появлений значения Xi в выборке назыв. частотой значения Хi, а отнош. Wi=Ni/N - относительной частной этого значения.

Опр7. Статистич. распределением (или статис-м рядом) выборки назыв. табл., в верх. строке которой указано значен. выборки, а в нижней соответствующие им частоты или относит-ые частоты.

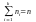
Аналог в теории вер-ти - ряд распределения.

Опр8. Полигоном относительных частот выборки назыв. ломанная в верш. в точках(Xi;Wi). Аналог в теории – многоуг. распределения.

Опр9. Групированым статис-м рядом выборки назыв. табл., в верх строке которой указаны интер-лы(либо их границы), а в нижней - соответ-щие им относительн. частоты.

Замечание! В качестве относит-ной частоты, соответ-щей итервалу, принимаюит сумму относит-х частот тех значений выборки, которые попали в этот интервал. Обычно интервалы берут одинаковой длины.

Замечание! Группир. ряд используется в тех случаях, когда число различных элементов выборки, т.е. число вариантов достаточно велико.

Опр10. Гистограммой назыв. графическое изображ. группир-го статистического ряда выборки.

Замечание!Для построения гистограммы по оси Ох откладыв. интервалы группир-го ряда и строят на каждом интервале как на основании прямоугольник, высотой Wi

Опр11. Эмпирическая функция распределения назыв. функцию F*(x), определенную формулой F*(x)=E_xi<x Wi, где суммируются относительные частоты Wi тех значений Xi из выборки, которые меньше х.

Замечание. При большем обьеме выборки эмпирич-кая функция распредел. F*(x) будет близкой к неизвестной теоретической функции распределения F(x) наблюдаемой СВ Х.

Опр12. Выборочной средней –х назыв. среднее арифметическое значение выборки. -х=1/n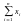 ( явл-ся оценкой для матем-го ожидания СВ Х)

Замечание! Если выборка представ-на статистич рядом то: -x=1/n*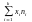

Опр13. Выборочной дисперсией D* (или S²) назыв среднее арифмит-кое квадратов отклонения значений выборки от выборочной средней

D*=1/n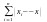 (явл-ся оценкой для дисперсии СВ Х)

Замечание. Если выборка представлена статистич-м рядом, то:

D*=1/n*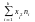 -(-x)²

Опр14. Выборочным СКО назыв. квадр. Корень из выбор-ной дисперсии:

.

Лекция 13. Статистические гипотезы.

Опр.1. Статистич гипотезой наз-ся любое предположение о виде или параметрах неизв закона распред-я Н,Н₀,Н₁…

Различают простую и сложную гипотезу. Простая гипотеза в отличие от сложной полностью опред теоретич ф-ю распред-я СВ.

Опр.2 Проверяемую гипотезу наз нулевой и обозн Н0. Конкурирующей(альтерн) наз гипотезу Н1,которая противоречит нулевой.

Проверка гипотезы. Гипотезу проверяют на основании выборки, сделанной из генер сов-ти. Из-за случайности выборки в рез-те проверки могут возникать ошибки и приниматься неправильные решения. Возможны ошибки 2х видов: 1)ошибка I рода (отвергнута гипотеза Н0,в то время, когда она верна 2)II рода (принята гипотеза Н0,в то время, когда она неверна.

(ТАБЛ)

Опр.3. Правило,по *ому гипотеза Но отвергается или приним наз-ся статическим критерием или критерием.

Обозн. α-вер-ть ошибки Iрода,β-вер-ть ошибки IIрода.

Опр.4.Вер-ть α наз-ся уровнем значимости критерия.Вер-ть 1-β наз-ся мощностью критерия.

В основе любого стат критерия лежит использ-е спец подобранные ф-и выборки,наз статистикой. Õ_n= Õ_n(Х1,Х2…Xn)

Когда статистика выбрана,мн-во ее возможных зн-й разбивают на 2 непересек подмн-ва:

1)Обл-ть принятия гипотезы (допустимая обл-ть)-подмн-во знач-й статистики,при *ых гипотеза Но приним-ся.

2)Критическая обл-ть (W)-подмн-во знач-й статистики,при *ых гипотеза Но отвергается.

Осн. принцип проверки стат гипотез. Если наблюдаемое зн-е статистики Õ_n принадл критич обл-ти,то гипотезу отвергают. Если оно принадл обл-ти принятия гипотезы,то гип приним.

Виды критич обл-тей. В зав-ти от вида альтерн гипотезы выбирают правостор,левостор,двустор. критич обл-ть. При этом границы критическаих областей Qкр, при заданном уровне значимости α, опред из соотношения.

1)Для правостор критич обл-ти P{Õ_n>θ_кр}=α 2)Для левостор критич обл-ти P{Õ_n<θ_кр}=α 3)Для двустор критич обл-ти P{Õ_n<θ_кр1}=P{Õ_n>θ_кр2}= α/2

Проверка гипотезы по зн-ю неизв параметра норм распред-я

Гипотеза о среднем. Пусть СВ Х распред по норм закону с пар-рами μ,σ.

Х Е N(μ,σ),где μ неизв. Требуется при уровне значимости α проверить гипотезу Но={μ=μ0(число)}. Предполож,что σ известно, тогда в кач-ве статистики критерия использ СВ. Z=(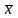 -μ₀)*√n/σ Е N(0,1). При этом

1)если Н1={ μ< μ₀}то использ левостор W,*ая удовл условию P{Z<-z_α}=α, (гр)

где z_α нах-ся из ур-я Ф(z_α)=1-α,где Ф(x)-ФР нормир норм распред-я

2) если Н1={ μ>μ₀},то использ правостор W,*ая удовл условию P{Z>z_α}=α, (гр)

где z_α нах-ся из ур-я Ф(z_α)=1-α

3)если Н1={ μ≠μ₀},то использ двустор W,*ая удовл условию P{!Z!>z_α}=α, где z_α нах-ся из ур-я Ф(z_α)=1-α/2 Зам.Если σ неизв,то в кач-ве статистики использ СВ t=( - μ₀)√n /S,*ая имеет распред-е Стьюдента с числом степеней свободы n-1,где n-объем выборки. При этом критич обл-ти опред так же,как и при известном σ,но вместо табл норм распред-я исп-ся табл распред Стьюдента.

Гипотеза о дисперсии. Пусть СВ Х распред по норм закону с парам μ и σ., т.е. Х Е N(μ,σ),где σ неизв. Нужно при уровне значимости α проверить гипотезу Но={σ²=σ²_{0(число)}}. Тогда в кач-ве статистики критерия использ СВ

χ²=(n-1)S²/σ²₀. Для опред W использ таблицы χ²-распред-я (р. Пирсона), при это

1.если H₁={δ ² <δ² ₀} , то исп левостор критическая область, а критич значение X_£ определяется по табл из условия P{ χ² >X_£}= 1 -£

2если H₁={ δ ² >δ² ₀} то исп правостор критическая область, а критич значение X_£ определяется по табл из условия P{ χ² >X_£}= £

3если H₁={ δ ² ≠ δ² ₀} то исп духсторонняя критическая область, а критич значение X_£ ‘ и X_£ “ определяется по табл из условия P{ χ² >X_£ “}= £/2

P{ χ² >X_{£ ‘}}= 1 - £/2

Лекция 12. Оценка паарметров распределения.

Пусть требуется изучит колич-ный признак Х генеральной совок-ти ( СВ Х) допустим, что из теорит-х соображений нам удалось установить сам вид з-на распред-ния ( нормальный , показательный и т.д.), но остается неизвестным один или несколько параметров распр-ния, например это параметр Y в распределении Пуассона. Таким образом для окончательного установления з-на распределения нам необходимо "Оценить", т.е. " Приближенно определить значение параметра распр-ния по некоторой выборке х1,х2,...,хn/

Замечание! Элементы выборки х1,х2,,..,,хn можно рассматривать как частные значения n независимых СВ Х 1,Х2,..,Хn каждое из которых имеет точно такой же з-н распределения, как и сам признак Х. Это объясняется тем, что различные серии опытов выборки будут различными.

Обознач. неизвестные параметры ч\з Q.

Опр1. Оценкой Qn или Tn параметра Q назыв. любая функция от рез-тов наблюдения над СВ Х, т.е. 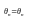(X1,X2,…,X_n).

Замечание. Поскольку X1,X2,…,X_n – СВ, то и оценка -Q_n в отличие от оцениваемого параметра Q является СВ.

Опр2. Оценка -Qn параметра Q назыв. несмещенной, если ее МО равно оцениваему параметру, т.е. M(Q_n)=Q. В противном случае оценка назыв. смещенной.

Замечание. Требование несмещенности гарантирует отсутствие систематич. ошибок при оценивании.

явл-ся несмещ. оценкой для

Примеры несмещенных оценок:

Опр3. Оценкой Qn параметра Q наз. состоятельной, если она удовлетворяет закону больших чисел, т.е.

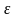для люб. >0

Опр4. оценка -Qn параметра Q назыв. эффективной, если при заданном объеме выборки она имеет наименьшую дисперсию,т.е. D(Q_n)=D_min

Опр5! Доверительной вероятностью или надежностью оценки Qn параметра Q назыв. вероятность 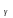, с которой осуществляется неравенство,

Заменив нер-во равносильным ему двойным неравенством Q_n- получим . Это соотношение следует понимать так: вероятность того, что интервал заключает в себе (покрывает) неизвестный параметр Q=

Опр6. Интервал ,который покрывает неизвестный параметр Q с заданной надежностью назыв. доверительным интервалом.

Замечание! Обычно надежность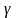 задается заранее, значением близким 1.( 0,95;0,98..)

Доверительный интервал для параметров нормального распределения.

Пусть колич-ный признак Х генеральной совок-ти СВ Х имеет нормальное распределение с параметрами 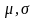т.е X

Предположим, что в рез-те наблюдения рад признаком Х, получена некоторая выборка х1,х2...хn, тогда:

1. доверительный интервал для Мо, (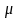 ), при известном ( ) имеет вид

Здесь: -х – выбороч средняя, n – объем выборки,пар-р U –определ из уравн.

Ф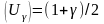 где Ф(U )- ф-ция распределения нормиров. распред. (табулированного)

- надежность

2) ! Доверит. интервал для Мо, при неизменном имеет вид

( x-t *S/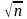 ;x+t *S/ ); х – выбороч средняя, n – объем выборки, S²-исправленная дисперсия, t –определяя по табл распрделен стьюдента

3) Доверит интервал для дисперсии S² имеет вид (((n-1)S²)/U₂ ; ((n-1)S²)/U₁)

n- обьем

S²- исправ дисперсия

U₁ и U₂(U₂>U₁) находятся из табл (хи квадрат распределения Пирсона) для заданной надежности

Лекция 16. Закон больших чисел

Предварительные замечания

Как известно, нельзя точно предсказать какое возможное значение примет СВ в результате испытания, между тем оказывается, что при некоторых весьма общих условиях суммарное поведение достаточно больш. числа СВ почти утрачивает случайный характер и может быть предсказанным с большой степенью определенности. Эти условия и указываются в теоремах, которые носят общее название закона больших чисел.

Закон больших чисел.

Лемма Чебышева: если СВ Х принимают только неотрицательные значения и имеют МО, то для любого числа справедливо неравенство:

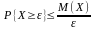
Доказательство: Введем в рассмотрение новую СВ:

Y= {0, <=x<E

{E, x>=E

При этом будет верно неравенство: 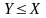. Следовательно ). Найдем теперь МО СВ У, её ряд распределения имеет вид.

Yi 0 E

Pi P{0<=x<E} P{x>=E}

Поэтому, M(Y)=0* P{0<=x<E}+E*P{x>=E}=E*P{x>=E}

Отсюда и нер-ва (*) получаем: E*P{x>=E}<=M(x) следов P{X>=E}<=M(x)/E

Теорема 1: (неравенство Чебышева)

Для любой СВ Х, имеющей МО и дисперсию, справедливо неравенство

Доказательство: Введем в рассмотрение новую СВ: Y=[X-M(X)]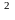 так как СВ Y>=0, то по Лемме Чебышева получаем: 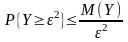или, что тоже самое: 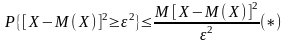с другой стороны

тогда неравенство (*) примет вид:

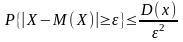
Следствие: Поскольку события 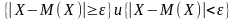противоположны, то неравенства Чебышева можно записать в виде:

Теорема 2: (теорема Чебышева) Если СВ попарно независимы и 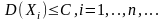где С – некоторая постоянная, то при любом 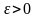справедливо равенство:

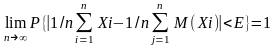
Доказательство: Введем в рассмотрение новую СВ 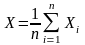найдем МО и оценку дисперсии СВ Х:

Запишем неравенство Чебышева в формуле (1) для СВ Х:

Зам: (смысл теоремы Чебышева): При большом числе n СВ практически достоверно, что их средняя хотя есть величина случайная, но она сколь угодно мало отличается от неслучайной величины 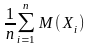, то есть практически перестает быть случайной.

Зам!: т. Ч-ва является наиболее общим законом больших чисел, а теорема Бернулли, рассматр-ая ниже, простейшим.

Т3: (теорема Бернулли): Пусть число успехов в n испытаниях Бернулли и р - вероятность появления успеха в каждом испытании, тогда при любом числе справедливо равенство:

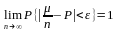
Доказательство: Воспользуемся след. представлением для СВ : 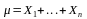, где - это ДСВ, означающая число появления успеха в i-ом испытании (i=1,2,3,….,n). Т. к. испытания Бернулли повторны и независимы, то СВ 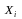(i=1,2,,….,n) будут попарно независимы и одинаково распределены, то есть будут иметь одинаковый ряд распределения.

Т.о. дисперсии СВ 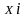(i=1,2,…,n) ограничены одной величиной, а значит к этим CD можно применить т. Ч-ва.

Центральная, предельная теорема.

Теорема 4: (центральная, предельная теорема).

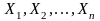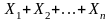Если независимые СВ, имеющие одно и тоже распределение с МО и дисперсией , то при неограниченном возрастании n, закон распределения суммы Х= , неограниченно приближается к нормальному.