Теория вероятности Лекция№1 Случайные события
Опр1: опыт, эксперимент, наблюдение явления будем называть испытанием.
Опр2: произвольное множества Ω (омега) называем пространством элементарных событий, а элементы ω (омега) этого множества будем называть элементарными событиями (элементарными исходами).
Замечание: элементарным событием соответствует взаимоисключающие исходы опыта (испытания).
НАПРИМЕР: испытание (S) – подбрасывание монеты 1 раз.
Элементарное событие: …-выпал герб
…-выпала решка……..
Опр3: произвольное подмножество пространство элементарных событий называется случайным событием или просто событием. Обозначают: А, В, С…
НАПРИМЕР: S-подбрасывание 1 раз игральной кости
Омега= {1,2,3,4,5,6}. Событие – А={выпало четное число очков}={246}
Опр4: говорят, что в результате испытания осуществилось (наступило) событие А, если произошло элементарное событие ω Є А.
Операции над событиями
Опр5: суммой событий А и В называется событие С, состоящее из всех элементарных событий, которые входят или в событие А или в событие В или в то и другое. Обозначают: С = А + В или С = A U В.
Замечание: событие А + В состоит в том, что произошло по крайней мере одно из двух событий А или В.
Опр6: произведением событий А и В называется событие С, состоящее из всех элементов, которые одновременно входят в обои события А и В. Обозначают: С = АВ или С = А ∩ В.
Замечание: событие АВ происходит тогда и только тогда, когда происходят одновременно и событие А, и событие В.
Опр7: разностью событий А и В называется событие С, состоящее из всех элементарных событий, которые входят в А, но не входят в В. Обозначают: С = А – В или С = А\В.
Виды случайных событий
Опр8: пространство элементарных событий называется достоверным, а пустое множество называется невозможным событием.
Опр9: события А и В называются несовместными, если их произведение есть невозможное событие, т. е. АВ = Ø, в противном случае события называются совместными.
Замечание: несовместные события не могут наступить одновременно, а совместные могут.
Опр10: событие Ā = Ω – А называется противоположным событию А.
Замечание: событие Ā (не А) означает, что событие а не произошло.
Говорят, что соб
А входит
в соб В, или соб А влечет за собой соб В
и пишут: А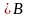
,
если все эл-ые события мн-ва А входят в
В
Св-ва операций над событиями:
1) А+
=Ω
2) А
=Ø
3) (А+В)С=АС+ВС
4)
=
*
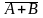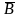5)
=
+
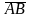6)
А*Ω=А
Классич. опред-е вер-ти
Вер-ть Р(А) соб А равна отношению кол-ва эл-х событий m, входящих в состав события А к кол-ву всех возможных эл-х событий n:
Р(А)=|A| / |Ω|=M/n
З Символ |М| обозначает число эл-в любого конечного мн-ва М (мощность мн-ва) З! Классич. опред-е вер-ти примен-ся тогда, когда:
1) простр-во эл-х событий Ω конечно, т.е. |Ω|=n (конечное число)
2)все эл-ые события ωi- равновер-тны (равновозможны), т.е Р(ωi)=1/n для ¥ i=1,2…n
Св-ва вер-ти:
1)Р(ω)=1 2)Р(Ø)=0 3) 0≤Р(А) ≤1 , для ¥ А 4)Р( )=1-Р(А) 5) АсB =>Р(А) ≤ Р(В) 6) А и В несовместны, то Р(А+В)= Р(А)+ Р(В)