6.Исследование поведения функции

Ебанная хуета, никто ебать не сделал этот вопрос. Охуели.

7.Неопределенный интеграл

1. Определение неопределенного интеграла

Если функция F(x) – первообразная для ф-ии f(x) на промежутке [a,b] , то множество ф-ий F(x)+C, где С – произвольная постоянная, называется неопределенным интегралом от ф-и f(x) на этом промежутке и обозначается символом ∫f(x)dx=F(x)+C

При этом ф-я f(x) называется подынтегральной ф-ей, f(x)dx – подынтегральным выражением, а переменная х – переменной интегрирования.

Св-ва неопределенного интеграла:

___________________________________________________

Список интегралов элементарных ф-ий

также

также

8 Способы интегрирования

Подведение под знак дифференциала

Данный метод эквивалентен методу замены переменной

Метод замены переменной (метод подстановки)

Интегрирование выражений вида

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.

Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.

Если n и m чётные, то удобнее сделать подстановку tg x = t.

Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:

Или:

В частности, с помощью n-кратного применения этой формулы находится интеграл

где — многочлен -ой степени.

9 Интегралы от некоторых функций содержащих квадратный трехчлен

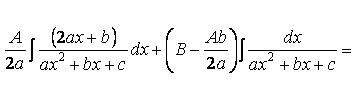
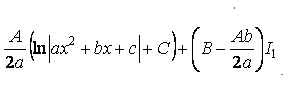
10 Интегр рац дробей

P(x)/Q(x) = (P₀ + P₁x + P₂x² + … + P_nxⁿ)/(Q₀ + Q₁x + Q₂x² + … + Q_mx^m)

Рациональная дробь называется правильной, когда n<m, во всеъ остальных случаях дробь называется нерпавильная.

Сведение дроби неправильной к сумме.

Теорема. Пусть x = a является корнем знаменателя кратности k (Q(x) = (x-a)^k,G(x)), тогда дробь P(x)/Q(x) может быть представлена виде (A/(x-a)^k) +

11 Интегрирование от некоторых иррац функций

Чтобы вычислить интеграл необходимо избавиться от иррац-ти.Основной метод-введение новой переменной.

1.R1=f(x,x^m\n)dx d ‘в этом случае избавиться от ирр-ти можно заменой x=t^j,j общий знаменатель дробей.2.R2=f(x,(ax+b\cx+d)^m\n)dx- cnfylfhnyfz

pfvtyf t^j=ax+b\cx+d,где jобщий знаменатель дробей m\n...3.R3(подстановки эйлера) 1подст.если а>0,то замена

2подст. с>0,замена

3подст. rогда есть 2 корня. , где — один из корней.

12 Интегрирование некоторых классов тригонометрических функций.

T1=∫f(cosX,sinX)dX.

Для таких интегралов рекомендуется воспользоваться формулами универсальной подстановки:

1) sinX=2t/1+t^2;

2)cosX=1 - t^2/1+t^2;

3)tgX=2t/1-t^2;

Для ctgX=2t/1-t^2;

Для всех 4 формул:

t = tg (X/2);

X = 2arctg(t);

dX= 2dt/1+t^2

T2=∫f(sinX)cosXdX= ∫f(t)dt;

T3=∫f(tgX)dX=∫f(t)/1-t^2

T4=∫f(cos^2n X,sin^2n X)dX;

Если подынтегральная функция имеет только четные степени,то рекомендуется сделать замену :

t=tgX; dX= dt/1+t^2/

13 Определенные интегралы(свойства интегральных сумм)

Нижние и верхние интегральные суммы.

Пусть на отрезке (а,b) задана функция f(X). Будем для определенности считать что f(X)>0;

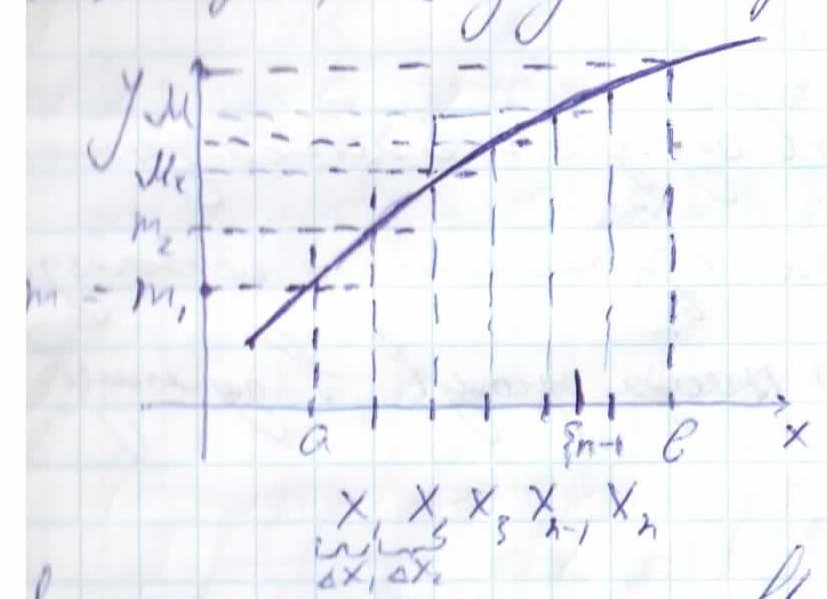
Разобьем (a,b) на ‘n’ производных частей.Пусть на отрезке (a,b) min=m;max=M; m=m1.

m1*△X1+m2*△X2+.........+mn*△Xn=∑mi*△Xi=Sn;

Приведенная сумма называется нижней интегральной суммой.

M1*△X1+M2*△X2+.........+Mn*△Xn=∑Mi*△Xi=Sn( Sn подчеркнута наверху)

Приведенная сумма называется верхней интегральной суммой:

Свойства интегральных сумм.

1)Sn≤Sn(c верхним подчеркивание)

m≤M;

2) Sn≥m(b-a);

3) Sn( с верхним подчеркивание) ≤M(b-a)

4)При увеличении числа промежутков (a,b) путем добавления точек деления, то Sn будет увеличиваться, а Sn( с верхним подчеркиванием) будет уменьшаться.

5) Верхняя и нижняя сумма при неограниченном числе производных стремится к некоторому пределу:

lim Sn = S. При n→∞

lim Sn(с верхним подчеркиванием) = S(с верхним подчеркиванием)При n→∞

6)Если функция f(x) непрерывна на заданном отрезке [a;b], то пределы верхней и нижней интегральных сумм равны ,при условии ,

7)Пусть s и S соответствуют разбиению отрезка [a;b] на и отрезков соотв-но, тогда

8)Если f(x) непрерывна [a;b], тогда при любом подходе к разбитию отрезка [a;b], (путем добавления новых точек деления), если ,тогда S и s будут стремится к пределу S (исходя из свойства 6)