1. Непрерывность функции

Пусть на некотором промежутке определена функция f(x), внутри промежутка лежит x = c, будем рассматривать f(x) как некоторую переменную y, которая упорядочена независимой переменной x.

1) x->c - 0

2) x->c + 0

3) x->c 0

Пусть y имеет вид:

1) =y(x)=A₁=y(c-0)

2) =y(x)=A₂=y(c+0)

3) =y(x)=A₃=y(c+-0)

если lim 3 существует, а lim 1 и 2 равны lim 3, то говорят, что функция непрерывна в точке c.

2 Производная и дифференциал

Производная функции

Пусть f(x) непрерывна в точке x₀. Производная этой функции называется lim приращения функции к приращению ее аргумента.

Дифферинцальность функции

Если функция f(x) в точке x = x₀ имеет производную, т.е. в точке имеет место

то говорят, что функция f(x)

дифференцируема в точке x0=x.

Таблица дифференциалов:

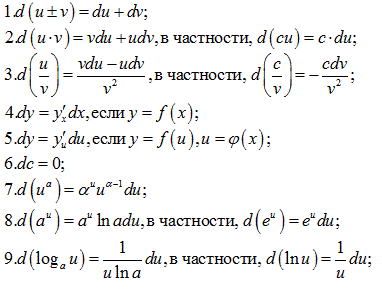
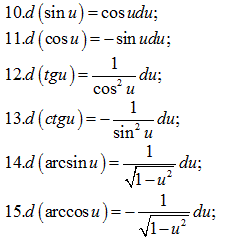
3 Свойства производной функции

1 Производная пост. вел = 0:

f(x)=c f’(x)=с=0

2. Пост. сомножитель возможно вынести за знак производной:

y(x)=c*f(x)

y’(x)=(c*f(x))’=c*f’(x)

3. Производная суммы (разности) конечного числа диф-мой функции=сумме (разности) производных этой функции:

Y(x)=f(x)+g(x)

Y’(x)=(f(x)+g(x))’=f’(x)+g’(x)

4. Производная от произведения 2-х диф-мых функций определяется следующим выражением:

Y(x)=f(x)*g(x) Y’(x)=f’(x)*g(x)+g’(x)*f(x)

5. Производная отношения 2-х диф-мых функций :

6. Если функция Y является функ.сложной, т.е. y(x)=y(z), где z=z(x) , то:

y’(x)=y’(z)*z’(x)

4 Неявная функция и ее дифф

1.1 F (x,y) = 0, если при постановке в это уравнение, функция y = f(x) обращается в тождество то функция определенного уравнения называется неявной.

Правило вычисления производной неявной функции совпадает с правилом вычисления функции явной, но y = y(x)

1.2 Обратная функции и производные обратных функций

y = f(x), тогда x = φ(y) - обратная к y = f(x)

Теорема Пусть дана непрерывная монотонная функция на промежутке от А до В, пусть φ(y) обратная функция к данной функции причем x’ = φ’(y) ≠ 0, тогда производная обратной функции будет вычитаться по следующему правилу φ’(y) = 1/y’.

1.3 Логарифмическое дифференцирование

y = (sin(x))^{x^2}

ln y = ln (sin(x))^{x^2}

ln y = x² ln (sin(x))

(1/y)*y’ = 2x ln (sin(x)) + x² (1/sin(x)) cos(x)

y’ = (sin(x))^{x^2} : x(2ln (sin(x)) + x ctg(x))

(xⁿ)’ = n (x^n-1)

1.4 Параметрические заданные функции.

Пусть имеется 2 непрерывные монотонные y = ψ(t) и x = φ(t), t ∈ [T₁ , T₂]

Функция y = f(x) будет называться параметрическим, уравнения (1) параметрические уравнения, а t - параметр.

Теорема Пусть параметрически задана уравнением (1) функция, пусть в уравнениях (1) функции y(t) и x(t) имеют обратные функции, а также имеют производные, тогда производная y’_x = ψ’_t (t)/φ’_t(t)

Док-во:

y’(x) = ψ(t) = ψ(φ^-1(x))

y’(x) = ψ’_t (t)(φ^-1(x)) = ψ’_t (t)/φ’_t(t)

1.5 Дифференциал.

y = y(x)

y’ = (Δy/Δx); Δy/Δx = y’ + α

Первое слагаемое - главное приращения Δy или дифференциал.

dy = y’(x)Δx; dy = y’(x)dx

y(x) = x

y’(x) = 1

y’(x)Δx = y’(x)dx

Δx = dx

Дифференциал независимого первого x совпадает с его приращением.

Из второго утверждения следует, что производная функции может быть определена как отношение приращения функции к дифференциалу независимой переменной x.

Δy = dy + αΔx | : Δy

1 = dy/Δy + αΔx/Δy

= +

1 = (dy/Δy) + (α/y’(x))

1 = dy/Δy + α/y’(x))

dy ~ Δy

Правило вычисления дифференциалов.

Задача нахождения дифференциала функции равносильна нахождению производной функции.

Свойства дифференциалов функции совпадают со свойствами производных. Большинство теорем и формул сохраняют свою силу и для дифференциалов.

Геометрический смысл дифференциала.

y’(x) = tg (α) = (Δx/Δy)

dy/dx = y’(x) = tg (α)

dy = y’(x)dx = tg (α)dx = (α) Δx

Дифференциал функции равен приращению ординаты касательной х к кривой y = f(x) в точке х

1.6 Производная и дифференциалы низших порядков

Пусть задана y = f(x), пусть она дифференцируема на от А до В

y’ = f ‘(x) = φ (x)

φ’ = φ’(x) = g (x)

φ’ = f ‘’(x) = f⁽²⁾ (x)

g’ (x) = f ‘’’(x) = f⁽³⁾ (x)

Производная 3-го порядка от f(x) называется производной 1-го порядка от результат вычисления производной 2-го порядка функции f (x)

По аналогии с производной функции высшего порядка дифференциалы второго порядка, называется дифференциал от первого порядка.

d(dy) = d²y

dy= y’(x)dx

d³y = d(d²y)

d(y’(x)dx) = d²y

y’’(x)(dx)² + y’(x)d²x = d²y

y’’(x)dx² = d²y

d²y/dx² = y‘’ (x)

y’’’(x) = d³y/dx³