2.1.13 Угол между осью z и плоскость., проходящей через ось плунжера и нормальной к вектору главного момента
плунжер |
Суммарный момент Нм |
1й плунжер (угол 0) |
5,50 |
2й плунжер (угол 40) |
5,83 |
3й плунжер (угол 80) |
6,01 |
4й плунжер (угол 120) |
5,95 |
5й плунжер (угол 160 |
5,68 |
6й плунжер (угол 200) |
0,18 |
7й плунжер (угол 240) |
0,46 |
8й плунжер (угол 280) |
0,52 |
9й плунжер (угол 320) |
0,34 |
плунжер |
Суммарный момент Нм |
1й плунжер (угол 0) |
0,213286248 |
2й плунжер (угол 40) |
0,213286248 |
3й плунжер (угол 80) |
0,213286248 |
4й плунжер (угол 120) |
0,213286248 |
5й плунжер (угол 160 |
0,213286248 |
6й плунжер (угол 200) |
2,928306406 |
7й плунжер (угол 240) |
2,928306406 |
8й плунжер (угол 280) |
2,928306406 |
9й плунжер (угол 320) |
2,928306406 |
2.1.14 Основные уравнения для системы сил и моментов, действующих на плунжер
(2.22
)
-
длина опорной части поверхности плунжера
-
полная длина плунжера
плунжер |
Опорная длина плунжера м |
1й плунжер (угол 0) |
0,025 |
2й плунжер (угол 40) |
0,020844949 |
3й плунжер (угол 80) |
0,018634092 |
4й плунжер (угол 120) |
0,019401915 |
5й плунжер (угол 160 |
0,022789143 |
6й плунжер (угол 200) |
0,027210857 |
7й плунжер (угол 240) |
0,030598085 |
8й плунжер (угол 280) |
0,031365908 |
9й плунжер (угол 320) |
0,029155051 |
Рассчитаем уравнение (2.22) относительно Rx и Rr, в первом приближении при µ=0
Из уравнения (2.23) получим
Подставим выражение в (2.24)
плунжер |
Реакция Rr м |
1й плунжер (угол 0) |
606,1295752 |
2й плунжер (угол 40) |
504,7537186 |
3й плунжер (угол 80) |
418,8047193 |
4й плунжер (угол 120) |
451,9014082 |
5й плунжер (угол 160 |
560,1817707 |
6й плунжер (угол 200) |
6,33070924 |
7й плунжер (угол 240) |
42,09701668 |
8й плунжер (угол 280) |
50,95941649 |
9й плунжер (угол 320) |
26,14565341 |
Определим силу Rx
плунжер |
Реакция Rx Н |
1й плунжер (угол 0) |
-19,52596527 |
2й плунжер (угол 40) |
-158,0891205 |
3й плунжер (угол 80) |
-263,825068 |
4й плунжер (угол 120) |
-223,8564441 |
5й плунжер (угол 160 |
-85,26071811 |
6й плунжер (угол 200) |
0,445496637 |
7й плунжер (угол 240) |
5,896440533 |
8й плунжер (угол 280) |
7,886905323 |
9й плунжер (угол 320) |
2,860090518 |
2.1.15 суммарная сила трения в районе контакта плунжера с цилиндром
плунжер |
Суммарная сила трения в районе контакта плунжера с цилиндром Н |
1й плунжер (угол 0) |
29,33 |
2й плунжер (угол 40) |
17,33 |
3й плунжер (угол 80) |
7,75 |
4й плунжер (угол 120) |
11,40 |
5й плунжер (угол 160 |
23,75 |
6й плунжер (угол 200) |
0,34 |
7й плунжер (угол 240) |
2,40 |
8й плунжер (угол 280) |
2,94 |
9й плунжер (угол 320) |
1,45 |
2.1.16 с учетом значения силы трения определим осевые силы, действующие на каждый плунжер
плунжер |
Сила, действующая на каждый плунжер Н |
1й плунжер (угол 0) |
2616,56 |
2й плунжер (угол 40) |
2919,43 |
3й плунжер (угол 80) |
3077,38 |
4й плунжер (угол 120) |
3022,85 |
5й плунжер (угол 160 |
2778,51 |
6й плунжер (угол 200) |
-169,80 |
7й плунжер (угол 240) |
-424,41 |
8й плунжер (угол 280) |
-482,05 |
9й плунжер (угол 320) |
-316,01 |
2.1.17
определим
с учетом сил трения, действующей на
плунжер
плунжер |
Касательная нагрузка, с учетом сил трения Н |
1й плунжер (угол 0) |
604,06 |
2й плунжер (угол 40) |
673,98 |
3й плунжер (угол 80) |
710,45 |
4й плунжер (угол 120) |
697,86 |
5й плунжер (угол 160 |
641,45 |
6й плунжер (угол 200) |
-39,20 |
7й плунжер (угол 240) |
-97,98 |
8й плунжер (угол 280) |
-111,29 |
9й плунжер (угол 320) |
-72,95 |
2.1.18 Определим нормальную составляющую с учетом силы трения, действующей на плунжер
плунжер |
Касательная нагрузка, с учетом сил трения Н |
1й плунжер (угол 0) |
2685,39 |
2й плунжер (угол 40) |
2996,22 |
3й плунжер (угол 80) |
3158,32 |
4й плунжер (угол 120) |
3102,36 |
5й плунжер (угол 160 |
2851,60 |
6й плунжер (угол 200) |
-174,26 |
7й плунжер (угол 240) |
-435,58 |
8й плунжер (угол 280) |
-494,73 |
9й плунжер (угол 320) |
-324,32 |
2.1.19 Определим опрокидывающий момент для каждого плунжера
плунжер |
опрокидывающий момент для каждого плунжера Нм |
1й плунжер (угол 0) |
9,06 |
2й плунжер (угол 40) |
12,91 |
3й плунжер (угол 80) |
15,18 |
4й плунжер (угол 120) |
14,37 |
5й плунжер (угол 160 |
11,04 |
6й плунжер (угол 200) |
-0,50 |
7й плунжер (угол 240) |
-0,92 |
8й плунжер (угол 280) |
-0,96 |
9й плунжер (угол 320) |
-0,79 |
2.1.19 Определим вертикальную составляющую силы инерции вращательного движения
плунжер |
Вертикальная составляющая силы инерции вращательного движения Н |
1й плунжер (угол 0) |
0,00 |
2й плунжер (угол 40) |
9,55 |
3й плунжер (угол 80) |
14,63 |
4й плунжер (угол 120) |
12,86 |
5й плунжер (угол 160 |
5,08 |
6й плунжер (угол 200) |
-5,08 |
7й плунжер (угол 240) |
-12,86 |
8й плунжер (угол 280) |
-14,63 |
9й плунжер (угол 320) |
-9,55 |
2.1.21 определим опрокидывающий момент от центробежных сил инерции
плунжер |
опрокидывающий момент от центробежных сил инерции Нм |
1й плунжер (угол 0) |
0 |
2й плунжер (угол 40) |
0,04922 |
3й плунжер (угол 80) |
0,10774 |
4й плунжер (угол 120) |
0,08487 |
5й плунжер (угол 160 |
0,01631 |
6й плунжер (угол 200) |
0,00615 |
7й плунжер (угол 240) |
0,05914 |
8й плунжер (угол 280) |
0,07849 |
9й плунжер (угол 320) |
0,03012 |
2.1.22 Суммарная составляющая касательных сил
Где z – количество плунжеров;
Z=9
– количество
плунжеров в зоне нагнетания
-
количество плунжеров в зоне всасывания
=4
2.1.29 суммарный опрокидывающий момент
2.2.Силы, действующие на ротор насоса в районе распределительного золотника
2.2.1 площадь отверстия цилиндра, выходящего на торец блока (рис.2.3)
Где все размеры d1 и b показаны на рис (2.35)
2.2.2 Активная площадь со стороны цилиндра
2.2.3 Сила, действующая на ротор в районе цилиндра
В зоне нагнетания
В зоне всасывания
2.2.4 Суммарная сила, обусловленная действием давления
Где
–
количество плунжеров в зоне нагнетания
- количество плунжеров в зоне всасывания =5
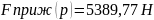
2.2.5 Сила отжатия ротора, действующая на перемычки блока между отверстиями цилиндров
Где
- площадь перемычки
Где z – количество плунжеров
2.2.6 Суммарная сила отжатия
2.2.7 Сила отжатия ротора, обусловленная давлением в зазоре между распределительным золотником и поверхностью блока цилиндра
2.2.8 Суммарная сила отжатия в зоне нагнетания
2.2.9 Суммарная сила отжатия в зоне всасывания
2.2.10 Сила трения, действующая со стороны плунжера в зоне нагнетания
Суммарная сила трения
2.2.12 Момент от сил трения и от сил давления, относительно оси ОУ
2.2.13 Момент от сил трения и от сил давления, относительно осей «OZ» на перемычку ротора
2.2.14 Момент от давления относительно сил «OY»
2.2.15 Момент в зоне нагнетания для внутренней и наружной полости
-среднее
давление в районе полоски
-
площадь полоски в зоне нагнетания
2.2.16 Суммарный момент относительно оси «OZ»
2.2.17 Суммарный момент
2.2.18 У ротора
2.2.19 Площадь внутренней рабочей поверхности
2.2.20 площадь наружной рабочей поверхности
2.2.21 Площадь перемычек между окнами
2.2.22 удельное давление
2.2.23 Внутренняя рабочая полоска
2.2.24 окружная скорость в районе рабочей полости
2.2.25 Наружная рабочая полоска
2.2.26 окружная скорость в районе полоски
Параметр нагрузки
– определяется
по статическим данным для насоса
3. Расчет устойчивости ротора насоса и расчет основных его элементов
3.1 Опрокидывающий момент (рис 3.1)
Где
- суммарная составляющая касательной
-
приведенная длина 0,01м
3.2 Условие устойчивости блока цилиндров
509,42>506.44 Нм
Условие устойчивости выполняется
3.3 Расчет вала (3.2)
3.3.1 Определение реакций опор Ra и Rbъ
Из формулы (3.4) определим Rb
3,4 изгибающий момент
3,5 определение угловой деформации
Площадь грузовой эпюры
3.6 Угол поворота
-
наружный радиус хвостовика
-внутренний
радиус хвостовика ротора
3.7 определение подшипников
3.7.1
– суммарная
нагрузка
3.7.2 Скорость скольжения
3.8 определение момента на валу
-
суммарный момент сопротивления
Где
- момент, обусловленный действием
касательной составляющей
– суммарный
момент сопротивления, обусловленный
действием сил трения в цилиндрах насоса
3.8.2Момент трения в подшипниках
Где R – радиальная сила, действующая в подшипнике
К – коэффициент трения
Где ∆- динамический зазор ∆=1 мм
-
- диаметр подшипника
-
удельная нагрузка подшипгика
b – рабочая ширина подшипника
n – число оборотов
3.9 суммарный момент трения в подшипниках
3.10
4. Расчет шлицевого соединения
4.1 Окружное усилие
Где
-
диаметр делительной окружности
4.2 Напряжения сжатия
где
- наружный диаметр шлиц 26мм
-
внутренний диаметр шлиц 24мм
z – число шлиц 20
b - рабочая длина шлиц 25мм
-
предел прочности на сжатие, для материала
Сталь 45
Материал вала сталь 20х – улучшенная, цементация и закалка, твердость поверхности 56...43 HRC. Цементация последующей закалкой наряду с большой твердостью поверхностных слоев обеспечивает и высокую прочность зубьев на изгиб.
4.3 угол закручивания
Где l – Длина участка l=25мм
G
–
модуль
упругости
5 Расчет контакта плунжера с наклонной шайбой
5.1 суммарное усилие
Где
–
усилие со стороны сепаратора
– центробежная
сила инерции подпятника
Где
Rп
–
радиус центра масс подпятника
m – масса подпятника m=0.00203кг
Остальные 4 можно не учитывать, т.к. они находятся на участке всасывания и малы в сравнении с силами на нагнетании
5.2 удельная нагрузка на поверхности подпятника
5.3 удельная нагрузка в зоне сферической головки плунжера
-
Условие выполняется
6. Расчет наклонной шайбы
6.1 выбираю первый тип шайбы.
6.2 Силы, действующие на наклонную шайбу
В основной системе координат
Определим
плунжер |
|
1й плунжер (угол 0) |
0,6565 |
2й плунжер (угол 40) |
0,6606 |
3й плунжер (угол 80) |
0,6628 |
4й плунжер (угол 120) |
0,6621 |
5й плунжер (угол 160 |
0,6587 |
6й плунжер (угол 200) |
0,6543 |
7й плунжер (угол 240) |
0,6509 |
8й плунжер (угол 280) |
0,6501 |
9й плунжер (угол 320) |
0,6523 |
плунжер |
|
1й плунжер (угол 0) |
-0,0280 |
2й плунжер (угол 40) |
-0,0214 |
3й плунжер (угол 80) |
-0,0049 |
4й плунжер (угол 120) |
0,0140 |
5й плунжер (угол 160 |
0,0263 |
6й плунжер (угол 200) |
0,0263 |
7й плунжер (угол 240) |
0,0140 |
8й плунжер (угол 280) |
-0,0049 |
9й плунжер (угол 320) |
-0,0214 |
плунжер |
|
1й плунжер (угол 0) |
0,0000 |
2й плунжер (угол 40) |
0,0180 |
3й плунжер (угол 80) |
0,0276 |
4й плунжер (угол 120) |
0,0242 |
5й плунжер (угол 160 |
0,0096 |
6й плунжер (угол 200) |
-0,0096 |
7й плунжер (угол 240) |
-0,0242 |
8й плунжер (угол 280) |
-0,0276 |
9й плунжер (угол 320) |
-0,0180 |
Выберем систему координат, связанную с шайбой. Для этого проведем через ось цапф плоскость, параллельную рабочей поверхности шайбы. В этой плоскости проведем оси Oz Yz через центр цапф шайбы, а ось Oz Zz – перпендикулярно ей. Ось OzXz проведем нормально плоскости YzOzZz.
В системе, связанной с шайбой, координаты точек Oi определяются по формулам
Где
-
расстояние
,
определяемое по чертежам
Определим
плунжер |
|
1й плунжер (угол 0) |
-0,2372944 |
2й плунжер (угол 40) |
-0,2372944 |
3й плунжер (угол 80) |
-0,2372944 |
4й плунжер (угол 120) |
-0,2372944 |
5й плунжер (угол 160 |
-0,2372944 |
6й плунжер (угол 200) |
-0,2372944 |
7й плунжер (угол 240) |
-0,2372944 |
8й плунжер (угол 280) |
-0,2372944 |
9й плунжер (угол 320) |
-0,2372944 |
плунжер |
|
1й плунжер (угол 0) |
-0,02800 |
2й плунжер (угол 40) |
-0,02145 |
3й плунжер (угол 80) |
-0,00486 |
4й плунжер (угол 120) |
0,01400 |
5й плунжер (угол 160 |
0,02631 |
6й плунжер (угол 200) |
0,02631 |
7й плунжер (угол 240) |
0,01400 |
8й плунжер (угол 280) |
-0,00486 |
9й плунжер (угол 320) |
-0,02145 |
плунжер |
|
1й плунжер (угол 0) |
-0,0548 |
2й плунжер (угол 40) |
-0,0363 |
3й плунжер (угол 80) |
-0,0265 |
4й плунжер (угол 120) |
-0,0299 |
5й плунжер (угол 160 |
-0,0450 |
6й плунжер (угол 200) |
-0,0646 |
7й плунжер (угол 240) |
-0,0797 |
8й плунжер (угол 280) |
-0,0831 |
9й плунжер (угол 320) |
-0,0733 |
(2.8)
плунжер |
Реакция со стороны наклонной шайбы, Н |
1й плунжер (угол 0) |
2906,64 |
2й плунжер (угол 40) |
2847,84 |
3й плунжер (угол 80) |
2698,94 |
4й плунжер (угол 120) |
2529,62 |
5й плунжер (угол 160 |
2419,09 |
6й плунжер (угол 200) |
-238,88 |
7й плунжер (угол 240) |
-128,38 |
8й плунжер (угол 280) |
42,49 |
9й плунжер (угол 320) |
189,86 |
плунжер |
Опрокидывающий момент, Нм |
1й плунжер (угол 0) |
-145,46 |
2й плунжер (угол 40) |
-102,28 |
3й плунжер (угол 80) |
-76,87 |
4й плунжер (угол 120) |
-85,89 |
5й плунжер (угол 160 |
-123,23 |
6й плунжер (угол 200) |
5,73 |
7й плунжер (угол 240) |
17,56 |
8й плунжер (угол 280) |
20,79 |
9й плунжер (угол 320) |
12,03 |
Суммарный момент
Опрокидывающая сила
Где
- плече усилия
Усилие Rc
Где
- угол между векторами Rc
и Rш
Определим проекции силы Rc на оси Oz Yz
6.2.3 определение реакций опор шайбы
Плоскость шайбы
Суммарные реакции на опорах шайбы
6.3 расчет опоры шайбы
Радиальные роликоподшипники с короткими цилиндрическими роликами
Где z- число роликов в одном ряду
– диаметр
ролика в мм
рабочая
длина ролика
6 Расчет каналов штуцера
Скорости входа и выхода:
– всасывание,
примем
,
нагнетание
Рабочий
объем жидкости:
Отсюда площадь канала всасывание и нагнетания (возьмем их с площадями) равно:
Получим
каналы входа и выхода с
.
Штуцер – MR 22x1,5
7 Расчет фланцевого соединения
Агрегат, присоединяемый к изделию – гидравлический мотор аксиально-поршневой по схеме Тома.
Заключение.
Результат расчета позволяет определить конструкцию расчета, соответствующую техническому заданию на расчет и проектирование.
В работе выполнена расчетная часть и спроектирована рабочая сборка