
- •Резисторы;
- •Конденсаторы;
- •Трансформаторы;
- •Основные законы электричества
- •Движение электронов в ускоряющем электрическом поле
- •Движение электронов в тормозящем электрическом поле
- •Движение электронов в поперечном электрическом поле
- •Движение электронов в магнитных полях
- •Поток электронов и условное направление тока
- •Разность потенциалов
- •Напряжение на участке цепи
- •Закон Ома для участка цепи, не содержащего э.Д.С.
- •Закон Ома для участка цепи, содержащего э.Д.С.
- •Действие электрического тока
- •Фундаментальные зависимости
- •Законы Кирхгофа
- •Магнетизм и электромагнетизм
- •Электромагнитная индукция
- •Взаимоиндукция
- •Лекция 2 Переменный ток
- •Резистор в цепи переменного тока
- •Катушка в цепи переменного тока
- •Конденсатор в цепи переменного тока
- •Закон Ома для электрической цепи переменного тока
- •Импеданс
- •Мощность в цепи переменного тока
- •Постоянная составляющая в сигнале переменного тока
- •Среднеквадратическое значение (действующее) переменного тока
- •Соотношение между пиковыми и среднеквадратическими значениями
- •Среднеквадратическое значение сложных сигналов
- •Лекция 3 Форма сигнала
- •Период (Цикл)
- •Частота
- •Скважность
- •Соотношение между частотой и периодом
- •Звуковые волны
- •Гармоники
- •Высота тона
- •Гармонические составляющие прямоугольного сигнала
- •Гармонические составляющие пилообразного сигнала
Лекция 3 Форма сигнала
Изменения тока или напряжения во времени можно представить в виде различных линий, или графиков. Постоянный ток, как неизменяющийся во времени, изображается прямой линией (рис. 3.1), а переменный ток — самыми различными кривыми. Форма кривой переменного тока отражает периодические изменения значения тока от максимального до минимального, затем опять к максимальному и т. д. (рис. 3.1). Несколько таких кривых показано на рис. 3.2.
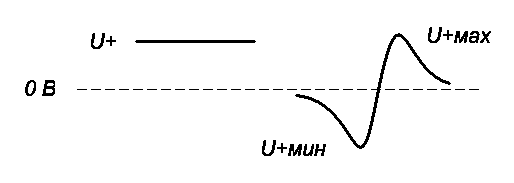
Рис.3.1
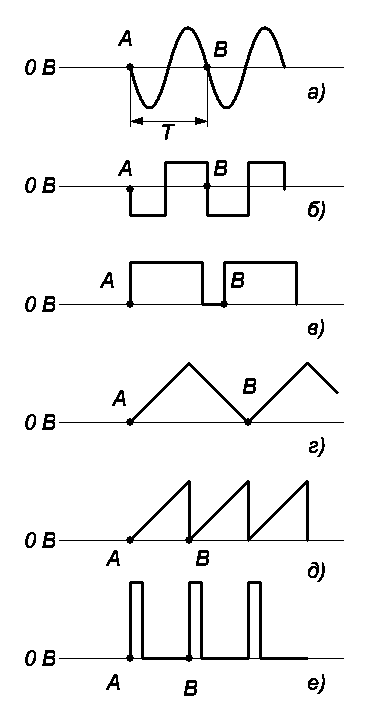
Рис.3.2 Типы кривых переменного тока:
а) синусоида; б) меандр; в) прямоугольный; г) треугольный; д) пилообразный; е) импульсы;
Период (Цикл)
Повторяющаяся часть сигнала переметного тока называется периодом (циклом) сигнала. Так, на кривых, изображенных на рис. 3.2, точка А является началом цикла, а точка В — его концом и началом следующего цикла. Время, за которое завершается полный цикл изменения сигнала, называется длительностью его периода Т или просто периодом. Например, если сигнал проходит все изменения за одну секунду, то его период равен 1 с, если за половину секунды, то период равен 0,5 с.
Частота
Количество периодов (циклов) сигнала в единицу времени называется частотой сигнала. Единица измерения частоты — герц (Гц). Например, если цикл изменения сигнала повторяется один раз в секунду, то частота сигнала равна 1 Гц, если 5 раз - 5 Гц рис. 3.3
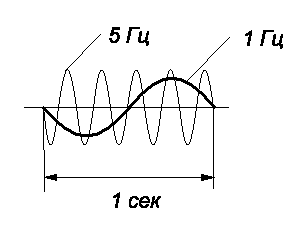
Рис.3.3
Скважность
Отношение периода следования (повторения) импульсов одной последовательности к их длительности называется скважностью. Величина, обратная скважности, называется коэффициентом заполнения. Таким образом, для импульсного сигнала справедливы следующие соотношения:
S = T/t1 = 1/D
где S — скважность, D — коэффициент заполнения, T — период импульсов, t1 — длительность импульса. Частое применение в практике находит сигнал со скважностью, равной двум — меандр.
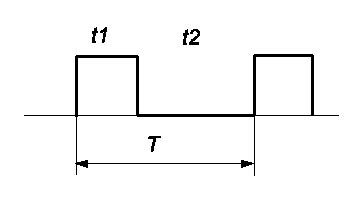
Рис.3.4
Соотношение между частотой и периодом
Рассмотрим графики сигналов на рис. 3.3. Период сигнала, частотой 5 Гц в 5 раз меньше, чем период сигнала частотой 1 Гц А. При увеличении частоты сигнала его период уменьшается, и наоборот.
Частота = 1/период (в герцах), или f = 1/T(в герцах),
Период = 1/частоту (в секундах), или Т = 1/f (в секундах).
Звуковые волны
Звуковые волны возникают в воздухе, например, когда кто-нибудь говорит или при работе громкоговорителя. Звуковые волны изменяют давление воздуха, и воздух необходим им для распространения. Интенсивность звуковых волн характеризуется громкостью, тон характеризует их частоту. При изменении частоты изменяется тон звука. Диапазон звуковых частот, которые воспринимаются ухом человека, называется диапазоном аудиочастот. Он простирается от 20 Гц до 20 кГц. Звуки частотой ниже 20 Гц и выше 20 кГц человек не слышит.
Гармоники
При сложении нескольких различных по частоте синусоидальных колебаний возникает сложное колебание. И наоборот, сложный сигнал можно разложить на ряд входящих в него чистых синусоидальных колебаний. Среди этих простых синусоидальных колебаний различают основную, или первую, гармонику и набор гармоник. Таким образом, любой сложный сигнал может быть разложен на следующие компоненты:
первая, или основная, гармоника. Простое синусоидальное колебание, имеющее тот же период, что и исходное сложное колебании;
набор гармоник. Простые синусоидальные колебания, частоты которых кратны частоте основной гармоники.
Например, если частота первой гармоники равна 100 Гц, то частота 2-й гармоники = 2×100 = 200 Гц, частота 3-й гармоники = 3 ×100 = 300 Гц, частота 4-й гармоники = 4×100 = 400 Гц и т. д. Чем больше номер гармоники, т. е. чем выше ее частота, тем меньше ее амплитуда. Поэтому высшими гармониками обычно пренебрегают.
