13. Уравнение момента количества движения.

Л.Эйлер распространил уравнение для момента количество движения твердого тела на жидкость. Это уравнение для жидкости формулируется так (см. рис.): момент равнодействующей всех внешних и внутренних сил, действующих на выделенный объем жидкости, относительно произвольно выбранной оси, равен секундному изменению момента количества движения массы выделенного объема жидкости относительно той же оси (т.е. секундному изменению момента количества движения жидкости, вытекающей из выделенного объема и втекающей в него):

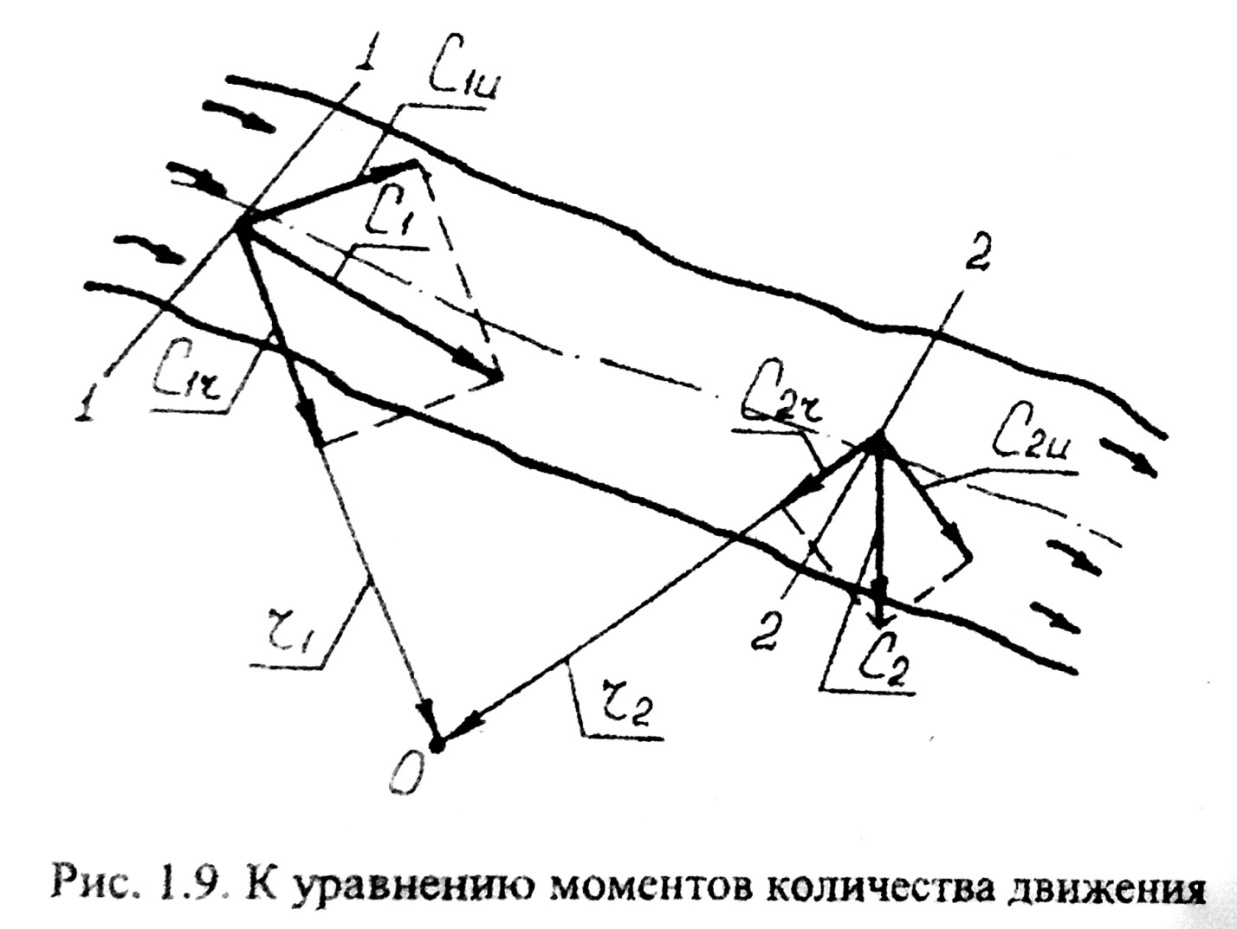
14. Пример использования уравнения момента количества движения в лопаточной машине.

15. Газодинамические функции.

В теории лопаточных машин и авиационных двигателей широко используются безразмерные скорости:

- число Маха – , где 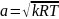- местная скорость звука;

- приведенная скорость , где ,критическая скорость.

Критическая температура и критическая скорость связаны с температурой торможения следующими соотношениями:

;

.

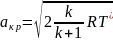Величины безразмерных скоростей (т.е. М и ) определяют характер течения рабочего тела в проточной части лопаточных машин. Практика показала, что во многих случаях целесообразно пользоваться некоторыми безразмерными функциями от чисел М и .

Рассмотрим некоторые газодинамические функции, используемые при расчете лопаточных машин.

Начнем с функции , представляющей собой отношение температур при отсутствии теплообмена. С целью получения выражения через М и воспользуемся уравнением сохранения энергии при отсутствии теплообмена и внешней работы.

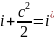или ,

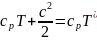Откуда

(1.12)

Разделим обе части уравнения (1.12) на T*:

.

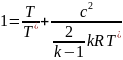Тогда

.

В последнем уравнении выразим через используя формулу (1.12) - . В этом случае

Или

И окончательно

(1.13)

Чтобы выразить через число Маха, величину подставим в виде, представленном формулой (1.12). Тогда

Разделим числитель и знаменатель правой части последнего уравнения на температуру T:

. (1.14)

Далее найдем выражение функции через М и . Для этого используем уравнение изоэнтропы . Тогда с учетом формулы (1.13)

(1.15)

Чтобы выразить через М, используем формулу (1.14):

. (1.16)

Функция представляет собой отношение .

Для изоэнтропического процесса

.

Поэтому

(1.17)

Или

(1.18)

Широко используемая газодинамическая функция q (приведенный расход) есть отношение плотности тока в потоке к максимально возможной плотности тока :

.

Но ; или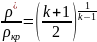 , тогда или с учетом уравнений (1.17) и (1.18):

(1.19)

(1.20)

Приведенный расход достигает максимального значения ( при (максимальная плотность тока). Увеличение и уменьшение от этого значения уравнение для определения расхода с помощью q( . С этой целью в выражении расхода G=cF произведение выразим через q. Если , то . Тогда

. (1.21)

Известно, что , а , поэтому уравнение расхода можно представить в таком виде:

(1.22)

Выполним преобразования и полученное выражение подставим в (1.22)

Обозначим

, тогда

(1.23)

Формулой (1.23) широко пользуются при расчете расхода газа.

Для воздуха при умеренных температурах:

k=1,4; R=287,3 Дж/кг*К; m=0,0404 . Используются и другие функции от .