1.3. Построение планов ускорений.

Определение линейных ускорений точек механизма происходит в той же последовательности, что и определение линейных скоростей (рис 1.3). Ускорение точки А кривошипа состоит из нормальной и тангенциальной составляющих:

.

По модулю :

Вектор нормального ускорения направлен вдоль прямой АО₂ от точки А к центру О₂ . Модуль тангенциального ускорения определится:

так как кривошип АО₂ вращается с постоянной угловой скоростью.

Выбрав полюс π и величину отрезка , изображающего вектор , определяют масштаб плана ускорений:

Откладывая вектор ускорения точки А из полюса π параллельно звену О₂А в направлении от А к О₂, обозначают конец вектора стрелкой и буквой а.

Переходя к первой двухповодковой группе, определяем ускорение точки В − кинематической пары, соединяющей звенья 3 и 4. Для ускорения точки В составляется система векторных уравнений:

,

.

С целью упрощения решения каждый вектор следует разложить на два составляющих вектора: нормального и тангенциального ускорений:

,

где ─ нормальная составляющая ускорения точки В при ее относительно вращательном движении вокруг точки А;

─ тангенциальная составляющая ускорения точки В при ее относительно вращательном движении вокруг точки А;

,

─ нормальная составляющая ускорения точки В при ее относительно вращательном движении вокруг точки О₃;

─ тангенциальная составляющая ускорения точки В при ее относительно вращательном движении вокруг точки О₃.

В систему векторных уравнений не вошли =0 и =0 по причине равномерного вращения точки А и неподвижности точки О₃.

Модули нормальных ускорений определяются по известным формулам:

; .

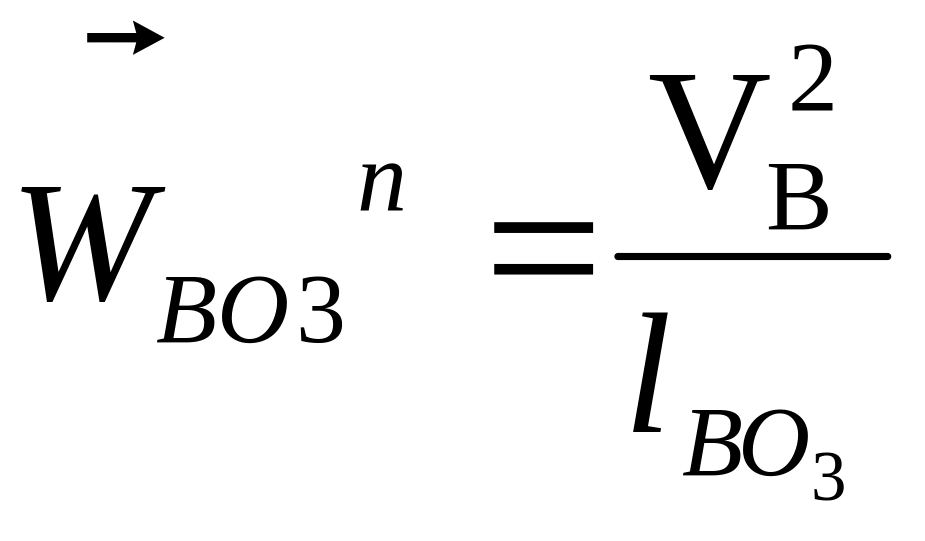Направлено нормальное ускорение параллельно звену АВ от точки В к точке А. Тангенциальное ускорение неизвестно по модулю, но известно по направлению. Оно направлено перпендикулярно звену АВ. Нормальное ускорение направлено параллельно звену О₃В от точки В к точке О₃, а тангенциальное ускорение − перпендикулярно О₃В.

Окончательно уравнение для определения ускорения точки В примет вид:

,

в котором два неизвестных параметра и , и которое может быть решено графически, путем построения плана ускорений.

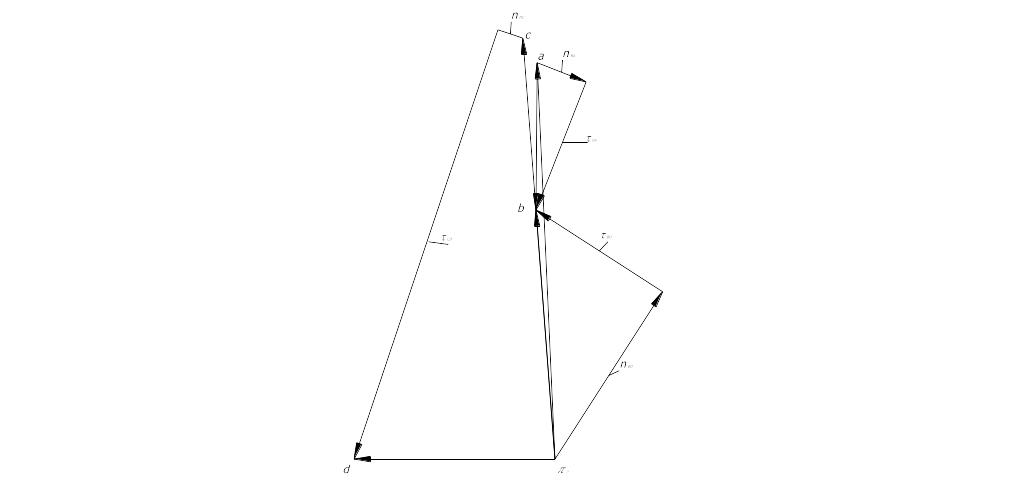
Рисунок 1.3 План ускорений.

На плане ускорений векторы нормальных , и касательных ускорений , будем для удобства записи обозначать .

Величины нормальных ускорений на плане определяем аналитически по формулам:

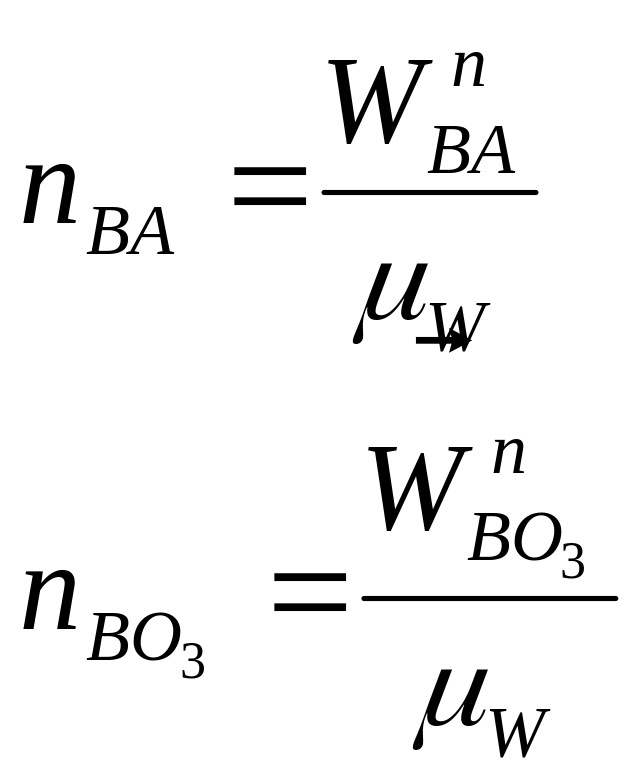
Через точку а плана ускорения (рис.1.3) проводим линию, параллельную звену АВ и откладываем на ней в направлении от точки В к точки А вектор . Это есть вектор относительного нормального ускорения . Через конец этого вектора проводим прямую, перпендикулярную звену АВ. Эта прямая является линией действия касательного ускорения .Затем нужно построить левую часть последнего уравнения. Для этого из полюса π проводим линию параллельную звену О₃В и откладываем на ней в направлении от точки В к точки О₃ вектор . Через конец этого вектора проводим прямую, перпендикулярную звену О₃В, которая является линией действия касательного ускорения . Пересечение линий, по которым действуют касательные ускорения и , позволяет получить точку в. Вектор изображает полное ускорение точки в, модуль которого равен:

.

Модули касательных ускорений:

; .

Ускорение W_ВА находится:

.

По теореме подобия находим ускорение точки с:

, откуда .

Модуль этого ускорения:

Ускорение точки д определяется, решая векторное уравнение:

,

─ нормальная составляющая ускорения точки D при ее относительно вращательном движении вокруг точки С;

─ тангенциальная составляющая ускорения точки D при ее относительно вращательном движении вокруг точки С.

В этом выражении векторы и известны. Вектор направлен от точки D к точке С, а модуль этого вектора определяем по формуле:

.

Кроме того, известно направление линии действия вектора − перпендикулярно прямой СD, и направление линии действия вектора − вдоль горизонтальной линии, по которой перемещается ползун.

Из точки с проводим вектор , параллельный звену CD:

,

направленный от точки D к точке С. Это есть вектор относительного нормального ускорения . Через конец этого вектора проводим прямую перпендикулярно звену DС. Эта прямая является линией действия касательного ускорения . Затем через полюс проводим прямую параллельно направляющей х-х. Точка пересечения двух прямых определит конец вектора .

Величина полного ускорения точки D определится по формуле:

.

Измерив затем длину вектора , находим модуль касательного ускорения:

.

Ускорение W_DC находится:

.

Угловые ускорения звеньев определяются на основе построенного плана ускорений. Ведущее звено вращается равномерно и .

Угловое ускорение звена 3 по модулю определится через тангенциальное ускорение:

,

а его направление укажет вектор , мысленно перенесенный с плана ускорений в точку В механизма. Условно закрепляя точку А звена 3, направление вектора покажет, что направлено против часовой стрелки. Звено 4 вращается с угловым ускорением , определяемым по формуле:

.

Направление углового ускорения ε ₄ находим перенося вектор в точку В механизма и рассматривая действие этого вектора относительно шарнира О₃. Как это видно из чертежа, звено стремится, как бы повернуться по часовой стрелке. Следовательно, в этом направлении действует .

Находим величину углового ускорения ε ₅ звена СD:

.

Направление его определяется аналогично и данном случае действует против часовой стрелки.

Для механизма, изображенного в положении 8:

Аналогично строится план ускорений для других 3 положений механизма, и полученные вычисления занесем в таблицу 1.2.

Таблица 1.2. Значения линейных и угловых ускорений точек и звеньев механизма.

Параметры	6	8	2	3
,	7,276
,	2,3977	0,9671	2,909	0,1798
,	2,6376	2,5234	26,7367	13,2154
,	0,0669	3,6509	11,579	2,7968
,	4,1025	2,766	16,2005	10,1249
,	4,1031	4,5804	19,9131	10,5041
,	3,6843	2,7016	26,8945	13,2167
,	0,9366	8,3173	32,5135	10,0032
,	6,9348	7,7415	33,6559	17,7743
,	0	0,483	1,529	0,1011
,	0,9366	8,3032	32,4776	10,0027
,	6,9978	3,6864	21,2968	18,6839
,	12,268	11,737	124,357	61,467
,	28,891	19,479	114,088	71,302
,	0,9366	8,3032	32,4776	10,0027