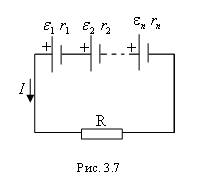
1-2)! .2. Последовательное и параллельное соединение источников тока

.

В общем случае при последовательном соединении нескольких источников с различными ЭДС сила тока определяется отношением суммы ЭДС всех источников тока к полному сопротивлению всей цепи:

,

где  – внутреннее сопротивление i-го источника, R – сопротивление нагрузки.

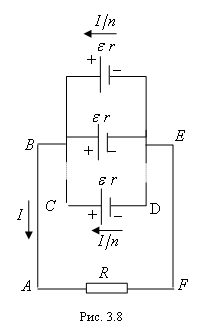
2)!

Последовательное соединение источников ЭДС,

.

Таким образом, при параллельном соединении n одинаковых элементов в батарею ЭДС не меняется, а внутреннее сопротивление уменьшается в n раз. Легко видеть, что параллельное соединение элементов выгодно при малом внешнем сопротивлении. Действительно, если , то им можно пренебречь, и формула приближенно принимает вид , то есть сила тока возрастает в n раз по сравнению с силой тока от одного элемента.

3-4)!

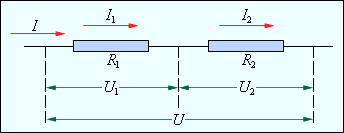
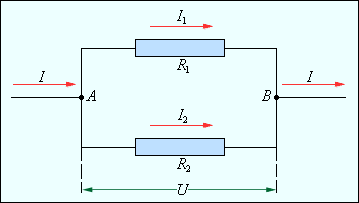
Законы последовательного и параллельного соединения проводников.

Проводники в электрических цепях могут соединяться последовательно и параллельно.     Последовательным, будем называть такое соединение при котором в каждой точке цепи соединяется только два проводника. Параллельным будем называть такое соединение при котором в точке цепи соединяется более двух проводников.     Последовательное соединение проводников (рис. 3.2.3.1) Рисунок 3.2.3.1. Последовательное соединение проводников.   1) Сила тока во всех последовательно соединенных проводниках одинакова:   I1 = I2 = I.   2) Общее напряжение  в последовательной цепи равно сумме напряжений на последовательных участках. В случае соответствующем рисунку 3.2.3.1., напряжение U на обоих проводниках равно сумме напряжений U1 и U2. действительно, по закону Ома, напряжения U1 и U2 на проводниках равны   U1 = IR1,   U2 = IR2.   U = U1 + U2 = I(R1 + R2) = IR,   где R – электрическое сопротивление всей цепи. Отсюда следует:   R = R1 + R2.   3) При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников. Этот результат справедлив для любого числа последовательно соединенных проводников.     Параллельное соединение проводников (рис. 3.2.3.2) Рисунок 3.2.3.2. Параллельное соединение проводников.   4) Напряжения на всех параллельных проводниках одинаковы. В случае соответствующем рисунку 3.2.3.2., напряжения U1 и U2 на обоих проводниках одинаковы:   U1 = U2 = U.   5) Сумма токов, протекающих по параллельным проводникам, равна току в неразветвленной цепи. Действительно, в точках разветвления токов (узлы A и B, рис 3.2.3.2) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,   I = I1 + I2.   Записывая на основании закона Ома где R – электрическое сопротивление всей цепи, получим 6) При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников. При параллельном соединении проводников действует простое правило - общее сопротивление параллельного участка, меньше меньшего. Т.е. если параллельный участок составляют резисторы сопротивлениями 3 и 5 Ом, то общее сопротивление будет меньше 3 Ом. Простой подсчет, по приведенной выше формуле, дает результат: 1,875 Ом.    Этот результат справедлив для любого числа параллельно включенных проводников.

7)!

Кхиргоф

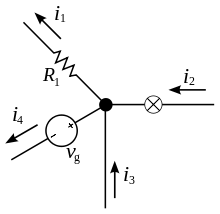
Первое правило

Сколько тока втекает в узел, столько из него и вытекает. i₂ + i₃ = i₁ + i₄

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

для постоянных напряжений

для переменных напряжений

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее)

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Пример

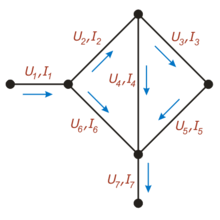
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

8)! Решение узловых и контурных уравнений

Узловые или контурные уравнения образуют линейную алгебраическую систему, имеющую общий вид

с матрицей A = G_у или R_к, неизвестными x = u₀ или i_к и вектором правых частей b = J_у

Численные методы решения узловых и контурных уравнений включают метод последовательного исключения Гаусса и его модификации, связанные с разложением матрицы А на треугольные матрицы, а также итерационные методы. Они подробно изложены в курсе численного анализа. 

Заметим, что наличие в алгоритмах этих методов операций вычитания может при вести к погрешности решения или трудностям при плохой обусловленности решаемых систем уравнений. Выше было показано, что матрицы, близкие к вырожденным, могут появиться при расчете активных цепей. Подобные затруднения встречаются и при расчете пассивных цепей со значительным разбросом параметров элементов. Пусть, например, в пассивной цепи два узла соединены ветвью с сопротивлением, существенно меньшим по сравнению с остальными сопротивлениями. В узловых уравнениях, составленных для обоих узлов, будут доминировать члены, включающие проводимость их общей ветви, и оба уравнения будут близкими друг к другу, что приведет к плохо обусловленной системе, решение которой с помощью стандартных методов может дать большие погрешности. Аналогичная ситуация возникает и при контурном анализе, если сопротивлении общей ветви двух контуров существенно больше остальных сопротивлении. Для преодоления возникающих трудностей можно перейти от узлового анализа данной цепи к контурному и наоборот. 

9)! Метод узлового напряжения

Порядок расчета цепей методом узлового напряжения:

1. Если по условию задачи задан реальный источник ЭДС, обязательно указываем на схеме его внутреннее сопротивление.

2. Расставляем направления токов в ветвях: все токи либо вытекают из узла, либо втекают в него.

3. Рассчитываем электрическую проводимость каждой ветви: g = 1/R (См).

4. Рассчитываем напряжение между узловыми точками по формуле: U_AB = (g)/g. В этой формуле ЭДС берется со знаком “+”, если ее направление совпадает с направлением тока в ветви.

5. Рассчитываем значения токов в ветвях по формуле: I_i = (_i – U_AB) g_i. В этой формуле ЭДС берется со знаком “+”, если ее направление совпадает с направлением тока в ветви.

6. Т.к. направления токов в ветвях были выбраны произвольно, то при расчете токи получаются алгебраическими величинами (либо положительными, либо отрицательными). Если какой-то ток получился отрицательным, это значит, что модуль его равен полученному значению, а действительное направление на схеме в противоположную сторону.

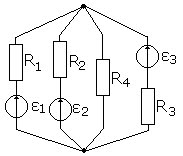Пример решения задачи:

₁ = 20 В; ₂ = 100 В; ε₃=80В; r_B1= rв2 = r_в3 = 0,5 Ом; R₁=9,5Ом, R₂=19,5Ом, R₃ = 3,5 Ом; R₄=10Ом

Задание: определить токи в ветвях

g₁ = 1/(R₁ + r_в1) = 1/(9,5 + 0,5) = 0,1 См

g₂ = 1/(R₂ + r_в2) = 1/(19,5 + 0,5) = 0,05 См

g₃ = 1/(R₃ + r_в3) = 1/(3,5 + 0,5) = 0,25 См

g₄ = 1/R₄ = 1/10 = 0,1 См

U_АВ = (₁g₁ + ₂g₂ + ₃g₃)/(g₁ + g₂ + g₃ + g₄) = (2 + 5 + 20)/0,5 = 54 В

I₁ = (₁ - U_АВ) g₁ = -3,4 А I₃ = (₃ - U_АВ) g₃ = 6,5 А

I₂ = (₂ - U_АВ) g₂ = 2,3 А I₄ = - U_АВg₄ = -5,4 А