3 . Техническое описание конструкции

Устройство обладает следующей конструкцией. Корпус из ударопрочного полистирола, габариты 25614070 мм³. На передней панели органы управления и индикации: ручка регулировки громкости, ручка настройки по частоте, снабженная индикатором, выключатель питания в виде кнопки. Конструкция приемника содержит 1 плату и динамическую головку. Плата крепится к корпусу винтами, указанными в спецификациях. Этим обеспечивается защита от внешних механических воздействий. Для обеспечения теплового режима задняя стенка крышки перфорирована.

4 . Расчеты

4.1. Компоновочный расчет

4.1.1. Общий внутренний объем корпуса

V_=49,547,525=58781,25 см³;

4.1.2. Найдем коэффициент заполнения корпуса

К=V_к/V_=29390/58781,25=0,39770,5.

Таким образом, эти расчеты показали, что коэффициент заполнения в нашей конструкции соответствует требованиям, предъявляемым к стационарной приемной аппаратуре.

4.2. Расчет тепловых режимов РЭС

4.2.1. Площадь поверхности корпуса блока S_K

S_К=2[L₁L₂+(L₁+L₂)L₃]= 2[0,4950,475+(0,495+0,475)0,255]=0,965 м².

4.2.2. Условная поверхность нагретой зоны S_З

S₃=2[L₁L₂+(L₁+L₂)L₃K₃]=2[0,4950,475+(0,495+0,475)0,2550,5]=0,718 м².

4.2.3. Удельная мощность корпуса блока РЭС Q_K

Q_K=P_З/S_K=700/0,965=725,39 Вт/м²,

где P₃ - тепловая мощность, рассеиваемая внутри корпуса (P₃ =700 Вт).

4.2.4. Удельная мощность нагретой зоны Q₃

Q₃=P₃/S₃=700/0,718=974,93 Вт/м².

4.2.5. Коэффициент перегрева корпуса блока K_qk

K_qk=0,147Q_K-0,0003Q_K²+0,310^-6Q_K³=

=0,147725,39-0,0003725,39²+0,310^-6725,39³=63,283.

4.2.6. Коэффициент перегрева нагретой зоны

K_q3 =0,139Q₃-0,0001Q₃²+0,710^-7Q₃³=

=0,139974,93-0,0001974,93²+0,710^-7974,93³=105,333.

4.2.7. Коэффициент K_H1, зависящий от атмосферного давления вне блока H₁=40 кПа _,

K_H1 =0,82+1/(0,925+4,610^-5H1)=0,82+1/(0,925+4,610^-54010³)=1,182.

4.2.8. Коэффициент K_H2, зависящий от давления воздуха в корпусе блока Н₂ =80 кПа,

K_H2=0,8+1/(1,25+3,810^-5H₂)=0,8+1/(1,25+3,810^-58010³)=1,033.

4.2.9. Площадь перфорационных отверстий S_п=0.007 м². Тогда коэффициент перфораций

П=S_п/L₁L₂=0,007/(0,4950,475)=0,03.

4.2.10. Коэффициент К_п , зависящий от коэффициента перфораций,

К_п=0,29+1/(1,4+4,95П)=0,29+1/(1,4+4,950,03)=0,936.

4.2.11. Перегрев корпуса блока РЭС

_К=0,93К_н1К_qkК_п=65,112 K.

4.2.12 Перегрев нагретой зоны

₃=0.93K_П[K_qkK_Н1+K_q3/(0,93-K_qK)]K_Н2=

=63,641 K.

4.2.13. Средний перегрев воздуха в блоке

_В=0,6₃=38.185 K.

4.2.14. Удельная мощность элемента

Q_ЭЛ=Р_ЭЛ/S_ЭЛ=1,6/0,012=133,

где Р_эл - мощность, рассеиваемая элементом, S_эл - его площадь вместе с теплоотводом.

4.2.15. Перегрев поверхности элемента

_ЭЛ=₃(0,75+0,25Q_ЭЛ/Q₃)=49,907K.

4.2.16. Перегрев среды, окружающей элемент

_ЭС=_В(0,75+0,25Q_ЭЛ/Q₃)= 29,944 K.

4 .2.17. Температура корпуса блока РЭС

T_k=_K+T_С=378.112 K,

где T_c- температура окружающей блок среды(Т_С=40).

4.2.18. Температура нагретой зоны T₃

T₃=₃+T_С=376,641 K;

температура поверхности элемента

T_ЭЛ=_ЭЛ+T_С=362,907 K;

средняя температура в блоке

T_В=_В+T_С=351,185 K;

температура окружающей элемент среды

T_ЭС=_ЭС+T_С=342,944 K.

4.3. Оценка показателей безотказности РЭС

4.3.1. В результате испытаний N устройств, проводившихся в течении времени t_и=1000 ч получены следующее данные о наработках до отказа.

Таблица 1

Интервалы наработки ti ,ч	000- 100	100- 200	200- 300	300- 400	400- 600	600- 800	800-1000	N
Число отказов ni	44	40	40	25	22	19	10	200

Таблица 2

Вид распределения	Критерий согласия	Характер восстановления
Усеченная нормальная	Пирсона	Ремонтируемая

Таблица 3

N	80
	0.8
	0.1
	0.1
Tи , ч	200	Ремонтируемая РЭС
R	10	Неремонтируемая РЭС

Таблица 4

Номер отказа	1	2	3	4	5	6	7	8	9	10	11	12
Время, ч	5	7	9	12	20	25	30	37	40	66	87	93
Номер отказа	13	14	15	16	17	18	19	20	21	22	23	24
Время, ч	109	124	131	146	147	151	159	162	177	184	192	199

В ычислим значения и построим графики статистических оценок вероятностей безотказной работы P_i^*(t), плотности наработки на отказ f_i^*(t) и интенсивности отказов _i^*(t) используя приведенные ниже формулы.

Полученные данные занесем в следующую таблицу.

P _i^*=1-n_i/N

P₁^*=1-44/200=0.78 P₂^*=1-84/200=0.58

f_i^*=n_i/(N*t_i)

f₁^*=30/(130*100)=0.0023 f₂^*=33/(130*100)=0.0025

_i^*=n_i/(N_iСР*t_i)

N_1СР=(200+156)/2=178 N_2СР=(156+(156-40))/2=136

₁^*=30/(115*100)=0.0026 ₂^*=33/(83.5*100)=0.0039

Интервалы наработки ti ,ч	000-100	100-200	200- 300	300- 400	400- 600	600- 800	800-1000	N
Число отказов ni	44	40	40	25	22	19	10	2000.0560000000000000000000000000000000000000000
Pi*	0.78	0.58	0.38	0.255	0.145	0.05	0
fi*	0.0022	0.002	0.002	0.00125	0.00055	0.000475	0.00025
NiСР	178	136	96	63.5	40	19.5	5
i*	0.00247	0.002941	0.004167	0.003937	0.00275	0.004872	0.01

где P_i^* , f_i^* , _i^* - статистическое значение вероятности безотказной работы, плотности наработки на отказ и интенсивности отказов на i-м интервале времени наблюдений

n_i - число отказов на i-м интервале

N - число изделий в начале испытаний

n_i - суммарное число отказавших изделий к началу i+1 - го интервала

t_i - продолжительность i -го временного интервала

N_iСР - среднее число работоспособных элементов на i - м интервале.

Г истограмма P_i^*=(t_i):

До этого сделал000000000000000000000000000000

Гистограмма f_i^*=(t_i):

Гистограмма _i^*=(t_i):

Проверим гипотезу о виде распределения, рассчитав предварительно точечные оценки параметров распределения.

Точечные оценки математического ожидания и дисперсии по экспериментальным данным можно вычислить по формулам

m_i^*= ; D_t^*= ;

m_t^*=1/200(50*44+150*40+250*40+350*25+500*22+19*700+10*900)=301.25

D_t^*=1/199[(50-301.25)²*44+(150-301.25)²*40+(250-301.25)²*40+

( 350-301.25)²*25+(500-301.25)²*22+(700-301.25)²*19+(900-301.25)²*10]=

=56945.66583.

При использовании критерия согласия Пирсона мерой расхождения теоретического и экспериментального законов распределения является сумма.

²= .

P_i - вероятность попадания случайной величины в i-ый интервал, вычисленная для предполагаемого распределения

P_i(t)=C₀ где С₀=1/[0.5+Ф(Т_ср/)].

Подставляя численные значения, получим:

C₀=1/[0.5+Ф(50/228.847)]=1,288

P₁(t)=1,288*0.77=0,75;

Интервалы наработки ti ,ч	000-100	100-200	200- 300	300- 400	400- 600	600- 800	800-1000
Pi(t)	0,75	0,459	0,374	0,342	0,130	0,019	0,001

²=(44-200*0.75)²/(200*0.75)+(40-200*0.459)²/(200*0.459)+

+(40-200*0.374)²/(200*0.374)+(25-200*0.342)²/(200*0.342)+

+(22-200*0.130²/(200*0.130)+(19-200*0.019)²/(200*0.019)+

+(10-200*0.001)²/(200*0.001)=689.479.

Исходя из полученных данных, можно утверждать, что гипотеза о виде распределения не верна.

4.3.2. По данным таблиц 2, 3, 4 оценим интенсивность отказов и для доверительной вероятности  найдем двухсторонний доверительный интервал

Для ремонтируемой аппаратуры используется план [n, M, t_и]

Время испытаний t_и определяется по таблице 3 , а количество отказов по таблице 4 из условия t_i t_и.

Суммарная наработка рассчитывается по формуле:

t_c=n*t_и=80*200=16000 ч.

^*=r/t_с=10/16000=0.000625 , где ^* - точечная оценка максимального правдоподобия

r = 10; tc = 16000;  = 0.8

 _н= =0,0018402

_в= =0,0009201

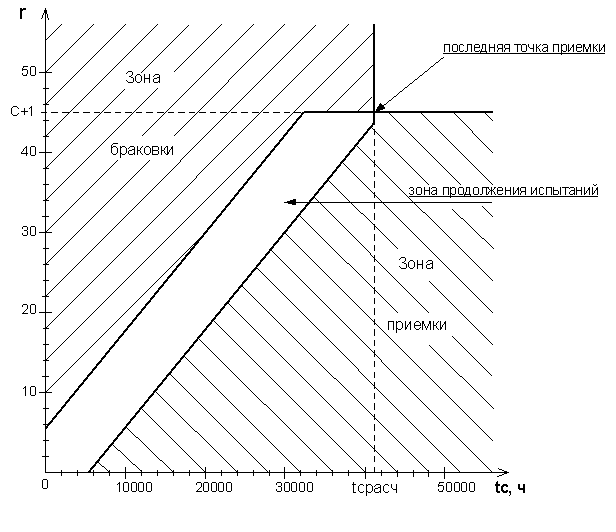
4.3.3. Рассчитаем усеченный план контрольных испытаний на надежность и построим графики границ областей приемки и браковки.

Поскольку для плана [n , M , t_и] суммарная наработка t_с неслучайная величина, распределение оценок параметра  будет определяться случайной величиной R(t) - количество отказов за время испытаний. Следовательно, проверку статистических гипотез H₀ и H₁ можно свести к проверке выполнения неравенства r C, где r -количество отказов за время испытаний, С - некоторое число называемое приемочным числом.

Испытания должны быть спланированы так, чтобы риски поставщика и заказчика не превышали заданные величины  и  соответственно:

=P[R(t_c)С/=_в] 

=P[R(t_c) C/=_н] 

Для планирования испытаний используется соотношение:

, где - квантиль распределения Пирсона уровня  с 2С+2 степенями свободы.

Приемное число С есть минимальное число из ряда 0,1,2,3,…, для которого предыдущее неравенство будет справедливо. Находится приемочное число методом подбора. Методом подбора установили С=44.

= = =1,95 2.

После определения приемочного числа необходимая суммарная наработка t_c находится из выражения , где , .

=17187,523 ч.

=65063,321 ч.

=41125,422 ч.

Для нахождения границ зоны приемки и браковки используем выражения

, , где A= =49,5, B= =0,01.

=43,755;

=56,85.