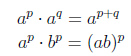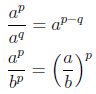Министерство образования и науки Оренбургской области.

Государственное автономное образовательное учреждения среднего, профессионального образования.

«Нефтяной техникум» города Орск.

Дисциплина математика.

Сообщение на тему:

«Степень с натуральным и рациональным показателем.».

Выполнил: студент 1курса

Группа М-158 Костин С.С.

Проверил: Яндович О.А.

Балл по выполнению:

2012

Степень с натуральным и рациональным показателем. Арифметический корень

С

тепенью с натуральным показателем n числа а называется произведение n сомножителей равных этому числу. - всего n сомножителей. Например, .

Число а называют основанием, а число n называют показателем степени. Степень с показателем 2 называют квадратом, а с показателем 3 – кубом. Примеры: Корнем n-ой степени (n-натуральное число) из числа a ( обозначение ) называют такое число x, степень которого равна a ( ).  Эту операцию называют извлечением корня n-ой степени из a. Корень из положительного числа – всегда число положительное. Корень второй степени не пишут, то есть . Например, , а не -2, хотя . Если число n – четное, то операция извлечения корня из отрицательного числа в поле действительных чисел не определена. Например, действительного числа не существует. Степенью с рациональным показателем m/n числа x (степенью с дробным показателем) называют число , m и n – целые числа.  Например, Любое число, кроме 0, в нулевой степени равно 1 . Операция не определена. Еще одно важное соотношение . Например:

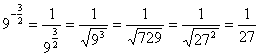
Степень с натуральным показателем {1, 2, 3,...}

Определем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).

1. По определению: .

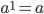2. Возвести число в квадрат — значит умножить его само на себя:

3. Возвести число в куб — значит умножить его само на себя три раза: .

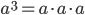Возвести число в натуральную степень — значит умножить число само на себя раз:

Степень с целым показателем {0, ±1, ±2,...}

Если показателем степени является целое положительное число:

, n > 0

Возведение в нулевую степень:

, a ≠ 0

Если показателем степени является целое отрицательное число:

, a ≠ 0

Прим: выражение не определено, в случае n ≤ 0. Если n > 0, то

Пример 1.

Степень с рациональным показателем

Если:

• a > 0;

• n — натуральное число;

• m — целое число;

Тогда:

Пример 2.

Свойства степеней

Произведение степеней
Деление степеней
Возведение степени в степень

Пример 3.

Корень

Арифметический квадратный корень

Уравнение имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.

Рассмотрим уравнение . Нарисуем график функции и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.

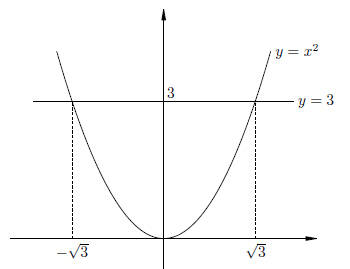
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.

Арифметический квадратный корень — это неотрицательное число, квадрат которого равен , a ≥ 0. При a < 0 — выражение не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу .

Корень из квадрата

Например, . А решения уравнения соответственно и

Кубический корень

Кубический корень из числа — это число, куб которого равен . Кубический корень определен для всех . Его можно извлечь из любого числа: .

Корень n-ой степени

Корень -й степени из числа — это число, -я степень которого равна .

Если — чётно.

• Тогда, если a < 0 корень n-ой степени из a не определен.

• Или если a ≥ 0, то неотрицательный корень уравнения 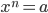называется арифметическим корнем n-ой степени из a и обозначается

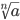
Если — нечётно.

• Тогда уравнение имеет единственный корень при любом .

Пример 4.

Таблица корней

Корень третьей степени (3)		Корень седьмой степени (7)
Корень четвертой степени (4)		Корень восьмой степени (8)
Корень пятой степени (5)		Корень девятой степени (9)
Корень шестой степени (6)		Корень десятой степени (10)

Основные свойства логарифмов

Скачать все правила одним файлом (PDF, 680 КБ)

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log_a x и log_a y. Тогда их можно складывать и вычитать, причем:

1. log_a x + log_a y = log_a (x · y);

2. log_a x − log_a y = log_a (x : y).

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:

Задача

Найдите значение выражения: log₆ 4 + log₆ 9.

Решение

Поскольку основания у логарифмов одинаковые, используем формулу суммы: log₆ 4 + log₆ 9 = log₆ (4 · 9) = log₆ 36 = 2.

Ответ

2

Задача

Найдите значение выражения: log₂ 48 − log₂ 3.

Решение

Основания одинаковые, используем формулу разности: log₂ 48 − log₂ 3 = log₂ (48 : 3) = log₂ 16 = 4.

Ответ

4

Задача

Найдите значение выражения: log₃ 135 − log₃ 5.

Решение

Снова основания одинаковые, поэтому имеем: log₃ 135 − log₃ 5 = log₃ (135 : 5) = log₃ 27 = 3.

Ответ

3

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

1. log_a xⁿ = n · log_a x;

2. 

3. 

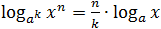
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача

Найдите значение выражения: log₇ 49⁶.

Решение

Избавимся от степени в аргументе по первой формуле: log₇ 49⁶ = 6 · log₇ 49 = 6 · 2 = 12

Ответ

12

Задача

Найдите значение выражения:

Решение

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2⁴; 49 = 7². Имеем:

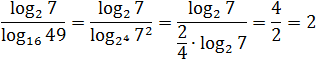
Ответ

2

Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log₂ 7. Поскольку log₂ 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.