1 Лабораторна робота 1

Дослідження методів апроксимації

Нелінійних функцій перетворення

Засобів вимірювань

Мета роботи – вивчення методів і засобів апроксимації нелінійних функцій перетворення засобів вимірювання, оволодіння практичними навич­ками апроксимації нелінійних функцій з використанням системи MATLAB.

1.1 Завдання для самостійної підготовки

1. Вивчити методи побудови аналітичних залежностей для експериментальних градуювальних характеристик вимірювальних перетво­рювачів і знаходження параметрів цих залежностей методом найменших квадратів [1, 2].

2. Ознайомитися з лабораторним завданням і вказівкою до його виконання.

1.2 Загальні відомості

Будь-який вимірювальний перетворювач, включений у вимірювальний ланцюг, реалізує певний вид перетворення вхідної величини x у вихідну величину y, який називається функцією перетворення

y=F(x). (1.1)

Основною вимогою, яка найчастіше висувається щодо функції перетворення, є лінійний характер залежності (1.1) в усьому діапазоні вимірювань. Якщо ж функція перетворення має суттєво нелінійні властивості, застосовують різноманітні методи її лінеаризації. В аналоговому вимірювальному приладі із стрілочним відліком це простіше всього зробити за допомогою нелінійної шкали, в якій реалізується обернена функція F^–1. В цифрових вимірювальних приладах, відліковий пристрій яких еквівалентний рівномірній шкалі, для усунення нелінійності застосовують такі способи лінеаризації [3]:

1) використання кодових нелінійних перетворювачів;

2) використання аналогових нелінійних перетворювачів;

3) суміщення операцій вимірювання і отримання оберненої нелінійної залежності F^-1 в одному пристрої – аналого-цифровому перетворювачі.

Універсальним методом зменшення впливу нелінійності функції перетворення на похибку результату вимірювання є алгоритмічна корекція функції перетворення. Для її реалізації необхідно в аналітичному вигляді представити рівняння перетворювача y=F(x) або x=F^-1(y) на основі експериментальних даних. Рівняння, яке описує експериментальні дані, але яке не можна отримати тільки теоретичним шляхом, називають емпіричною залежністю.

Знаходження емпіричних залежностей включає в себе два основних етапи:

1) встановлення загального вигляду емпіричної формули (структурна ідентифікація);

2) визначення параметрів залежності (параметрична ідентифікація).

Обґрунтований вибір загального вигляду залежності є доволі складною задачею, яка погано піддається формалізації, і здійснюється, виходячи з відомих фізичних законів, апроксимуючих можливостей вибраної функції та особистого досвіду проектувальника засобів вимірювання.

1.2.1 Апроксимація лінійних та нелінійних функцій методом найменших квадратів

Припустимо, що ми маємо експериментально отриману градуювальну характеристику вимірювального перетворювача (табл. 1.1), для якої необхідно отримати аналітичний вираз функції перетворення y=F(x).

Таблиця 1.1 – Градуювальна характеристика перетворювача

x	x1	x2	x3	. . .	xn
y	y1	y2	y3	. . .	yn

У випадку лінійної апроксимації емпіричної залежності необхідно визначити невідомі коефіцієнти b₀ і b₁ лінійної функції

y = b₀ + b₁x. (1.2)

Критерієм для знаходження параметрів b₀ і b₁ найчастіше виступає мінімум суми квадратів нев’язок теоретичної функції (1.2) і експериментальних даних

(1.3)

де оцінка величини y при підстановці в (1.2) значення x_i.

Мінімізація критерію призводить до розв’язання системи лінійних алгебраїчних рівнянь

(1.4)

Після визначення b₀ і b₁ потрібно обчислити нев’язки для кожного значення x_i:

На рис. 1.1 зображена лінійна апроксимація нелінійної градуювальної характеристики (кружечками зображено експериментальні дані , суцільною лінією – лінійна апроксимуюча функція).

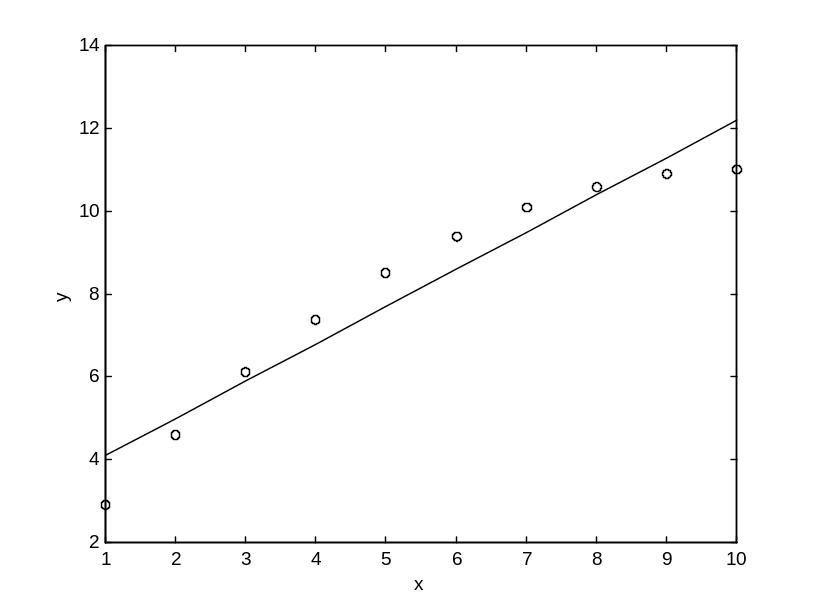
Рисунок 1.1 – Лінійна апроксимація нелінійної функції перетворення

Якщо отримані значення нев’язок не задовольняють дослідника, емпіричну залежність можна апроксимувати нелінійною функцією. Наприклад, функція має вигляд полінома другого порядку

(1.5)

Проведемо заміну змінних відносно яких функція (1.5) буде лінійною

Для знаходження невідомих коефіцієнтів можна скористатися методом найменших квадратів, при цьому система нормальних рівнянь (1.4) набуде вигляду

Знайдені значення коефіцієнтів підставляються у вихідну функцію (1.5).