1)Что такое функции, каковы способы задания функций.

Говорят что задана функция из множества Е в множество F, если каждому элементу из множества Е соответствует единственный элемент из множества F. Е-обл. определения ф-ции; F-множество значений или обл. значений ф-ции.

Как правило множества Е и F числовые. Способы задания ф-ций: 1)Табличный, в таблице перечисляются все значения ф-ции; 2)Графический, на плоскости указываются геом. объект состоящий из точек Х и У, где Х из обл. определения, а У из обл. значений; 3)Аналитический способ у=f(x). Не обязательно 1 формула задает ф-цию. Существует кусочный способ задания ф-ции. ( )

2)Что такое четная и нечетная ф-ции, как строить их графики.

у=f(x) - четная, если f(-x)= f(x). у=f(x)-нечетная, если f(-x) =-f(x). При этом надо иметь в виду в О.О.Ф. кроме значения х будет –х. Графики четной ф-ции симметричны относительно ОХ. Нечетной - симметричны началу координат.

Пр.

3)Что такое периодическая и обратная ф-ции, как строить их графики.

у=f(x)- периодическая, если существует Т: f(x+Т) =f(x), Т-период.

Пусть дана у=f(x), если х=f(у) и выразим У через Х, то получим ф-цию, которая называется обратной по отношению к исходной (у=f(x)). При этом О.О.Ф. и обл. значения меняются местами. Для существования обратной ф-ции необходимо, чтобы заданая ф-ция принимало каждое свое значение 1 раз. Графики прямой и обратной ф-ций симметрично прямой у=х. Пр.

4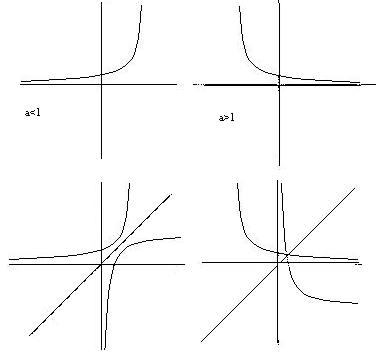 )Изобразить в графиках показательную и логарифмическую ф-ции при а<1, a>1.

Показательная: у=а^Х

при а>1-возрастает, при a<1-убывает.

Логарифмическая y=log_Ax (x=A^Y)

Логарифмическая ф-ция является обратной показательной.

5)Что такое гармоническая зависимость, каков вид ее графика.

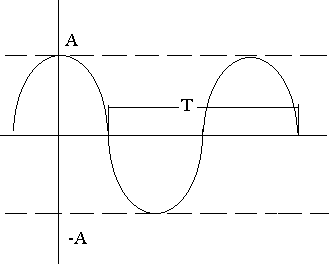-гармонические колебания ф-ции.

Где: T-период, зависит от .

 - сдвиг по оси Ох

6)Изобразить графики обратных тригонометрических ф-ций у=arcsinx, y=arccosx, y=arctgx, y=arcctgx

7)Что такое элементарная ф-ция.

Элементарной ф-цией называется любая ф-ция полученная из основных элементарных путем конечного числа операций сложения, вычитания, умножения, деления и образование сложной ф-ции - композиции.

Основные элементарные ф-ции: степенные(у=х^Р), показательные (экспоненциальные у=а^Х), логарифмические, тригонометрические, обратные тригонометрические.Неэлементарных ф-ций бесконечно много, как правило это кусочное задание ф-ций.

8)Как строить графики функций вида y=cf(x), y=f(cx), y=f(x)+c, y=f(x+c)

y=cf(x)- растягивается вдоль оси Оу при с>1, сжимается при 0<с<1 (sinx)

y=f(cx)- растягивается вдоль оси Ох при с<1, сжимается при с>1 (sinx)

y=f(x)+c- смещается вдоль оси Оу, при с<0-вниз, при с>0-вверх (х²)

y=f(x+c)- смещается вдоль оси Ох, при с<0-вправо, при с>0-влево (х²)

9)Что такое числовая последовательность, каковы способы её задания.

1 ,2,4,8,…,2^N-1

1 2 3 4 … N

a^N – общий член последовательности.

Это однозначно задает бесконечную числовую последовательность. Говорят, что задана бесконечная числовая последовательность, если всякому натуральному числу (номеру места) по какому-либо закону однозначно поставлено соответствие- определенное число (член последовательности). Способы задания числ. последовательности: (1)формулой общего члена последовательности;

(2)Рекуррентный способ- когда задается 1 или несколько первых членов последовательности и указывается способ, по которому последующий член последовательности выражается через предыдущий.(а₁=1 а_N=2а_N-1); (3)описательный способ (Последовательность десятичных приближений по недостатку для числа ); (4)Геометрический или графический.